(1-1-АГр)

Если Nоо, то в пределе получаем W (р) = е~Р. Уже при N = = 8 -f- 10 передаточная функция (14.8) мало отличается от передаточной функции звена с запаздыванием (14.6).

Уравнение любого линейного звена с запаздыванием (14.4) будем теперь записывать в виде

Q{p)xz = R (р) е-Рх. (14.9)

Передаточная функция линейного звена с запаздыванием будет

W{p)=-e-P = Wo{p)e-P, (14.10)

где через ip) обозначена передаточная функция соответствующего обыкновенного линейного звена без запаздывания.

Частотная передаточная функция получается из (14.10) подстановкой р = ]а:

W (/ю) = Wo (/со) e-i<- = Ao (со) еЛФо(а -та>] (14.11)

где Ао (to) и \ро {) ~ модуль и фаза частотной передаточной функции звена без запаздывания. Отсюда получам следующее правило.

Для построения амплитудно-фазовой характеристики любого линейного звена с запаздыванием нужно взять характеристику соответствующего обыкновенного линейного звена и каждую ее точку сдвинуть вдоль окружности по часовой стрелке на угол тсо, где со - значение частоты колебаний в данной точ- характеристики (рис. 14.4 а).

ному реальному звену, можно сравнить еще их амплитудно-фазовые характеристики с экспериментально снятой амплитудно-фазовой характеристикой звена, выражающей его динамические свойства при вынужденных колебаниях. Построение амплитудно-фазовых характеристик звеньев с запаздыванием будет рассмотрено ниже.

В целях единства записи уравнений представим второе из соотношений (14.4) для элемента запаздывания в операторном виде. Разложив правую часть его в ряд Тейлора, получим

или, в принятой ранее символической операторной записи,

(-т) = [1 +J= + ±I+ ... ++ = е-х,. (14.6)

Это выражение совпадает с формулой теоремы запаздывания для изображений функций (табл. 7.2). Таким образом, для звена чистого запаздывания получаем передаточную функцию в виде

W{p)= е-Р. (14.7)

Заметим, что в некоторых случаях наличие большого числа малых постоянных времени в системе регулирования можно учесть в виде постоянного запаздывания, равного сумме этих постоянных времени. Действительно, пусть система содержит N последовательно включенных апериодических звеньев первого порядка с коэффициентом передачи, равным единице, и вели-

ЧЕШОЙ каждой постоянной времени ДГ = . Тогда результирующая передаточная функция будет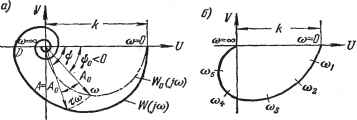

Рис. 14.4

между собой и с экспериментальной амплитудно-фазовой характеристикой реального звена надо принимать во внимание не только форму кривой, но и характер распределения отметок частот со вдоль нее.

Линейная система с запаздыванием. Пусть одноконтурная или многоконтурная автоматическая система в числе своих звеньев имеет одно звено с запаздыванием Тогда уравнение зтого звена имеет вид (14.9). Если таких звеньев несколько, то они могут иметь разные величины запаздывания (Ti, Та, . . .). Все выведенные в главе 5 общие формулы для уравнений и передаточных функций систем автоматического регулирования остаются в силе и для любых линейных систем с запаздыванием, если только в эти формулы подставлять значения передаточных функций в виде (14.10).

Например, для разомкнутой цепи из последовательно соединенных звеньев, среди которых имеется два звена с запаздыванием и Та соответственно, передаточная функция разомкнутой системы будет иметь вид

W (р) = Wo (р) e- Pe-sp = Wo (р) е-Сч+-2)р,

(14.12)

где Wo (р) ~ передаточная функция разомкнутой цепи без учета запаздывания, равная произведению передаточных функций включенных последовательно звеньев.

Таким образом, при исследовании динамики разомкнутой цепи из последовательно соединенных звеньев безразлично, будет ли все запаздывание сосредоточено в одном каком-нибудь звене или разнесено по разным звеньям. Для многоконтурных цепей получатся более сложные соотношения.

Если имеется звено с отрицательной обратной связью, обладаюней запаздыванием т, то Оно будет описываться уравнениями:

Qc (Р) Хвых = Rc (Р) (вх - Жос). Qoc (Р) ос = Roc (р) е-РХвых

(14.13)

Передаточные функции звена и цепи обратной связи будут при этом

wap)-

Дс (Р)

(14.14)

Так как в начале амплитудно-фазовой характеристики ю = О, а в конце сй=оо, то начальная точка остается без изменения, а конец характеристики асимптотически навивается на начало координат (если степень операторного многочлена R меньше, чем многочлена Q).

Выше говорилось о том, что реальные переходные процессы (временные характеристики) вида рис. 14!3, б часто могут быть с одинаковой степенью приближения описаны как уравнением (14.2), так и (14.5). Амплитудно-фазовые характеристики для уравнений (14.2) и (14.5) показаны на рис. 14.4, а и б соответственно. Принципиальное отличие первой состоит в том, что она имеет точку D пересечения с осью U. При сравнении обеих характеристик

Согласно (5.59) результирующая передаточная функция звена вместе с обратной связью будет

W(n\ с(Р) \FI у ос WI Н4 15

МР; i + Wc(p)Woc(p) Qc{p)QociP)+Rc(P)Roc(P)e-P

Этой передаточной функции соответствует дифференциальное уравнение звена в операторной форме

[1 + Wc (р) Woe (Р)] W = Wo (р) Жвх (14.16)

или, при подстановке (14.14),

[Qc (Р) Qcc ip) + ip) Roc ip) е-М Жых = Rc ip) Qoc ip) bx- (14.17)

Пусть, например, интегрирующее звено с замедлением, передаточная функция которого

iP) = рцХтр)

охватывается отрицательной обратной связью с передаточной функцией

Woo ip) = коов-Р.

Тогда результирующая передаточная функция звена с обратной связью в соответствии с (14.15) будет

W (р) =--~ .

Тр + р + коКсе-

Частотная передаточная функция получается подстановкой в последнее выражение р = /со:

W (/со)

Rc (Р) Qoc ip)

- Г(в2+/СО+кокосе icKc cos оэт-Та) +] [а-кокос sin сот)

Амплитудно-фазовая характеристика, соответствующая этому выражению, приведена для иллюстрации на рис. 14.5.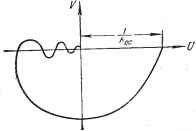

Рис. 14.5.

\0.С.\

Рис. 14.6.

Пример системы с запаздыванием. Рассмотрим систему регулирования скорости двигателя (рис. 1.16). Составим уравнения всех звеньев системы с учетом их инерционностей. Дополнительно к тому учтем еще запаздывание т в воздействии регулирующего органа на объект. Изобразим это введением в структурную схему данной системы дополнительного элемента запаздывания (рис. 14.6). Пусть объект не имеет самовыравнивания