Как и в случае замороженных коэффициентов, здесь приходится намечать опасные точки, где должно быть проведено исследование. Однако в рассматриваемом методе можно учитывать при этом не только сами значения коэффициентов в отдельные моменты времени, но и характер их изменения во времени (скорость изменения, ускорение изменения и т. д.). Это делает все исследование более полным при сохранении его относительной простоты.

В некоторых случаях оказывается более целесообразным отыскание и последующее замораживание переходной функции звена с переменными параметрами

(t - о) = К (т. о). (13.98)

Для переходной функции (13.18) может быть найдена передаточная функция

(р, 1&о) = Р j 2 о) е-Р dx. (13.99)

По сравнению с нахождением передаточной функции по замороженной весовой функции (13.94) здесь получается обычно более полный учет динамических качеств звена с переменными параметрами. Это оказывается наиболее заметным в тех случаях, когда в правой части дифференциального уравнения звена имеются переменные во времени коэффициенты. Их изменение может быть учтено только при нахождении переходной функции, так как при нахождении весовой функции значения коэффициентов в правой части уравнения фиксируются в момент приложения единичного импульса.

ГЛАВА 14

СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ И СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

§ 14.1. Уравнения линейных систем с запаздыванием

- Линейными системами с запаздыванием называются такие автоматические системы, которые, имея в общем ту же самую структуру, что и обыкновенные линейные системы (раздел II), отличаются от последних тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину т, называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса. Например, если обыкновенное линейное звено описывается уравнением

(14.1)

~Ь 2 -

(апериодическое звено первого порядка), то уравнение соответствующего линейного звена с запаздыванием будет иметь вид

ГГ dxzit)

+ Xzit) = kXi(t-T)

(14.2)

(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с запаздывающим аргументом или дифференциально-разностными уравнениями.

Обозначим X* (t) = Xi {t - т). Тогда уравнение (14.2) запишется в обыкновенном виде:

У -- х - кх*.

(14.3)

Так, если входная величина х изменяется скачком от нуля до единицы (рис. 14.1, а), то изменение величины х* = х {t - х), стоящей в правой части уравненмя звена, изобразится графиком рис. 14.1, б (скачок на т секунд позже). Используя теперь переходную характеристику обьшновенного апериодического звена в применении к уравнению (14.3), получаем изменение выходной величины Xz в виде графика рис. 14.1, в. Это и будет переходная характеристика апериодического звена первого порядка с запаздыванием (его апериодическое инерционное свойство определяется постоянной времени Т, а запаздывание - величиной т).

Линейное звено с запаздыванием. В общем случае, как и для (14.2), уравнение динамики любого линейного звена с запаздыванием можно

Рис. 14.1.

Q{p)x2R (р) X*, xt (t) =xi{t- т).

(14.4)

что соответствует условной разбивке линейного звена с запаздыванием (рис. 14.2, а) на два: обыкновенное линейное звено того же порядка и с теми же коэффщиентами и предшествующий ему элемент запаздывания (рис. 14.2, б).

Временная характеристика любого звена с запаздыванием будет, следовательно, такая же, как у соответствующего обыкновенного звена, но только сдвинута по оси времени вправо на величину т.

Примером звена чистого запаздывания т является акустическая линия связи (т - время прохождения звука). Другими примерами могут служить система автоматического дозирования какого-либо вещества, перемещаемого с помощью ленточного транспортера (т - время движения ленты на определенном участке).

Линейное звено с запозВы-Ванием

г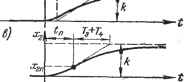

Рис. 14.2.

Рис. 14.3.

а также система регулирования толщины прокатываемого металла, где т означает время движения металла от валков до измерителя толщины. В двух последних примерах величина т называется транспортным запаздыванием.

В первом приближении определенной величиной запаздывания т могут быть охарактеризованы трубопроводы или длинные электрические линии, входящие в звенья системы (подробнее о них см. § 14.2).

Величину запаздывания т в звене можно определить экспериментально путем снятия временной характеристики. Например, если при подаче на вход звена скачком некоторой величины, принимаемой за единицу, на выходе получается экспериментальная кривая для х, показанная на рис. 14.3, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (14.2), взяв величины т, Г и А с экспериментальной кривой (рис. 14.3, б).

Заметим также, что такая же экспериыептальная кривая согласно графику рис. 14.3, е может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением

(Г -f- Tip -Ы) = (Гз7> -f 1) (Т + 1) 2 = кхх.

(14.5)

причем Ti, и ft можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами.

Итак, с точки зрения временной характеристики реальное звено, приближенно описываемое уравнением первого порядка с запаздывающим аргументом (14.2), часто может быть с такой же степенью приближения ошюано обыкновенным дифференциальным уравнением второго порядка (14.5). Для решения вопроса о том, какое из этих уравнений лучше подходит к дан-

разбить на два: