X (f) = 2 -р-Ц-ек. (13.78)

При наличии одного нулевого корня знаменателя изображения

Это будет передаточная функция системы с замороженными коэффициентами.

Для вычисления первой поправки {р, t) подставим полученное из (13.73) первое приближение в правую часть (13.70). Тогда получим для первой поправки

Формула для к~й поправки будет иметь вид

W,ip,t)=--SSP. (13.75)

Таким образом, последующий член ряда (13.72) получается посредством дифференцирования предыдущего члена в соответствии с (13.71) и подстановки его в (13.75).

Ряд (13.72) сходится тем быстрее, чем медленнее изменяются коэффициенты исходного дифференциального уравнения (13.1).

По найденной функции W {р, Z) может быть получена параметрическая частотная передаточная функция W (/о), t) подстановкой р = /со.

Использование параметрических передаточных функций. В соответствии с формулой (13.61) изображение Лапласа выходной величины системы с переменными параметрами можно найти как произведение изображения воздействия на параметрическую передаточную функцию:

X (р, t) = W (р, t) F (р). (13.76)

Это дает возможность находить переходные процессы в системе с переменными параметрами посредством использования преобразования Лапласа (или Карсона - Хевисайда). Для этой цели по формуле (13.76) отыскивается изображение выходной величины, а затем делается переход к оригиналу х {t).

Для этой цели могут использоваться существующие таблицы изображений Лапласа функций времени. Так, например, пусть изображение выхода ной величины равно

X{p,t)=Wip,t)Fip)= ,(,4+ .) .

Полагая в этом выражении время t фиксированным параметром, по таблице (см., например, табл. 7.2) находим

(0 = -ь7[1-е- +=>М.

Если изображение представляет собой сложную дробно-рациональную функцию, то можно использовать теорему разложения (см. § 7.4). При отсутствии нулевых корней знаменателя изображения

Х(Р) = Щ- (13.77)

аналогично формуле (7.37) получаем

§ 13.4]

УСТОЙЧИВОСТЬ и КАЧЕСТВО РЕГУЛИРОВАНИЯ

аналогично формуле (7.39) получаем

Xi {t):

(13.80)

В формулах (13.78) и (13.80) корпи знаменателя предполагаются некратными.

Для построения переходного процесса может также использоваться вещественная частотная характеристика (см. § 7.5). Для общего случая воздействия произвольной формы из (13.57), аналогично проделанному в § 7.5, можно получить расчетную формулу, являющуюся обобщением формулы (7.52):

Рф (со, t) sin at

(13.81)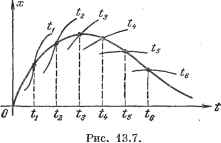

где Рф (со, t) - вещественная часть частотного изображехшя искомой фу1п?-цииж {t), полученного подстановкой в преобразование Карсона - Хевисайда р = /со.

В частном случае, когда входное воздействие представляет собой единичную ступенчатую функцию, из (13.57), аналогично проделанному в § 7.5, получается расчетная формула, являющаяся обобщением формулы (7.53) для переходной функции рассматриваемой динамической системы:

2 f Р (со, t) sin tot J a:(i)=A(0 = -j -da,

(13.82)

где P (со, t) - вещественная часть параметрической частотной передаточной функции (13.58).

Построение переходного процесса проводится, аналогично изложенному р § 7.5, по /j-функциям. Разница будет заключаться в том, что построение переходного процесса будет справедливым только для того момента времени t - const, который вошел в качестве параметра в параметрическую передаточную функцию. Поэтому необходимо построить серию кривых (рис. 13.7) для различных фиксированных моментов времени f t, ш т. д., а затем через точки, соответствующие этим значениям времени, провести плавную кривую.

Указанное обстоятельство значительно увеличивает объем вычислительной работы по сравнению с построением кривой переходного процесса в системе с постоянными параметрами.

§ 13.4. Устойчивость и качество регулирования

Для систем с переменными параметрами понятие устойчивости имеет некоторую специфику. Если система работает ограниченный интервал времени, то понятие асимптотической устойчивости (см. § 6.1) практически теряет свой смысл. Однако для квазистационарных систем при сравнительно медленном изменении коэффициентов уравнения (13.1) представляется возможным сформулировать понятие устойчивости следующим образом.

Будем считать систему с переменными параметрами устойчивой па заданном интервале времени Т, если ее нормальная функция веса (13.4) или

(13.5) затухает во времени для всех фиксированных значений лежащих внутри этого интервала. Это условие можно записать следующим образом:

со оо

It=\w{t-d,)\dt=\w{T,&)\dc<oo, 0<&<Г. (13.83) о

Если для системы получена нормальная функция веса, то вид ее и определяет устойчивость системы.

Однако в некоторых случаях имеется сопряженная функция веса (13.6) или (13.7), которая связана преобразованием Лапласа с параметрической передаточной функцией (13.62) и преобразованием Фурье с параметрической частотной передаточной функцией (13.58) или (13.59). Поэтому более просто мояшо исследовать вопрос затухания функции веса вдоль аргументов & (смещение) или 0 (реверс-смещение). Условие затухания вдоль этих аргументов можно записать следующим образом: t

и= j \w(t~-d, &)\df=\w{Q,t-Q)\dQ<oo, Q<t<T. (13.84)

-oo 0

Однако затухание сопряженной функции веса и выполнение условия (13.84) еще не означает затухания нормальной функции веса и вьшолнения условия (13.83). Заметим, что в системах с постоянными параметрами не наблюдается такой неопределенности, так как для них совпадают оба разреза рельефа функции веса: w (%) = w (6), и оба интеграла: It - определяемые формулами (13.83) и (13.84).

Можно показать [1181, что для систем, описываемых дифференциальным уравнением вида

aoit)+...+an {t)x = i{t),

выполнение условия (13.84) практически обеспечивает выполнение условия (13.83). В этих системах исследование устойчивости может быть проведено на базе параметрической передаточной функции.

Исследование затухания сопряженной функции веса может производиться как по ее виду, если она известна для рассматриваемой системы, так и на основании отсутствия полюсов параметрической передаточной функции замкнутой системы в правой полуплоскости и на мнимой оси. Для этой цели могут привлекаться известные критерии устойчивости, например критерий Михайлова, критерии Найквиста и др.

Формулы главы 5, дающие связь между передаточными функциями замкнутой системы Ф (/?), разомкнутой системы W (р) и передаточной функцией по ошибке Фдс (/)), сохраняют свою силу и для параметрических пере-даточшлх функций.

Качество регулирования может быть оценено по виду переходного процесса (переходной функции или функции веса) в соответствии с § 8.4. Для этой цели долншы использоваться нормальная функция веса и нормальная переходная функция, определяемые для фиксированного момента времени О < < Г.

Рассмотрим теперь точность воспроизведехшя задающего воздействия в следящих системах. Составим дифференциальное уравнение (13.1) так, чтобы в левой части находилась ошибка ж (f), а в правой - задающее воздействие g {t):

ао (t) + ... + й (О X (Z) = 6о it) +...+bm{t)g{t). (13.85)

Реакция системы на дельта-функцию в правой части g {t) - Ь {t - Ь. Щ представляет собой функцию веса ошибки Wx (t - &, &).