<4S+---+<2=- at+-..alx, . (13.49)

Это уравнение такне может быть решено с использованием преобразования Лапласа посредством нахождения оригинала изображения

где (р) - изображение у (t) нри подстановке в формулу (13.43) х = х.

Повторяя этот процесс многократно, моншо найти рекуррентное соотношение для определения к~то члена ряда (13.46):

+aUk= -Г< -+ +апХи-А . (13.50)

Ряд (13.46) сходится тем быстрее, чем медленнее изменяются коэффициенты Ui (t). Рассмотренный метод может использоваться как для пахожде-

где а? = at (&) - переменный коэффициент, зафиксированный для момента приложения входной величины Z = &.

Тогда исходное дифференциальное уравнение (13.1) можно представить в виде

< + < +---+aU = U{t)~y{t), (13.41)

fAt)=-h{t)+-.-+bmit)f, (13.42)

y(i) = <+...+fl*x. (13.43)

Поскольку мы предположили, что коэффициенты (О меняются медленно, то функция у {t) мала по сравнению с левой частью (13.41). Эту функцию можно рассматривать как возмущение, и тогда к уравнению (13.41) можно применить метод последовательных приближений.

В уравнении (13.41) можно перейти к изображениям по Лапласу. Тогда получим

Х{р) = Ф(р)Ро{р)-Ф{р)Г{р). (13.44)

Здесь введено обозначение

Решение уравнения (13.41) или (13.44) можно записать в виде ряда x{t)=xi + x2 + xg+ .. . (13.46)

Для получения первого приближения х зафиксируем переменные коэффициенты ai (J) = Ui ф). Тогда первое приближение может быть найдено как решение дифференциального уравнения

<4--Ь---+<1 = /о(0- (13.47)

Решение этого уравнения можно получить, используя обычные методы (см. главу 7), в том числе путем нахождения оригинала, соответствующего изображению (13.44) нри Y (р) = 0:

Хг (р) = Ф (р) Fo (р). (13.48)

Для получения второго приближения в правую часть (13.41) или (13.44) подставляется первое приближение х = х, а. в левую часть -х = х + х. Тогда получается уравнение с фиксированными коэффициентами для определения поправки:

ния функции веса и переходной функции, так и для построения переходного процесса при любом известном воздействии / (t).

Численно-графический метод. Численно-графический метод Д. А. Баш-кирова [98] разработан также применительно к системам с переменными во времени параметрами, причем можно вводить любое переменное возмущающее или задающее воздействие и произвольные начальные условия.

Неоднородные уравнения первого порядка с переменными коэффициентами. Пусть требуется построить рещение уравнения

во {t) X + ai{t)x = /i {t)

с начальным условием х = х при t = 0. Разделив его на % (f), приведем уравнение к виду

T{t)x + x=f (О,

(13.51)

о (о

1 ( )

ai(t)

Уравнение (13.51) можно решать графически, если считать Т постоянным и равным Tt-{-~ внутри каждого интервала времени {t, t + At), но различным для разных интервалов. Форму-

.j-m

ла для решения в этом случае будет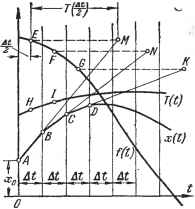

Рис. 13.5.

а процесс построения сводится к следующему. Наносим заданные кривые f {t) ж Т (t) (рис. 13.5). Из точки Е кривой / (f), взятой в середине первого интервала At, откладываем по горизонтали отрезок ЕМ =

величина которого берется равной ординате точки Н заданной кривой Т {t), т. е. тоже в середине первого интервала At. Полученная точка М соединяется прямой линией с заданной начальной точкой процесса А. В результате получается новая точка Б искомой кривой X (t). Затем аналогично берется ордината точки /, откладывается в виде отрезка FN и проводится прямая NB, дающая новую точку С решения X {t), и т. д.

Неоднородные уравнения второго порядка с переменными коэффициентами. Требуется построить решение уравнения

во (О х + а {t) X + 2 (О х = fi (t), которое можно записать также в виде

Г, {t) Tz (О x + Tz{t)x + x = f (t), (13.52)

с начальными условиями х = Хд, х Хд при = 0. Если в правой части (13.52) имеется операторное выражение, то предварительно производим вычисление правой части и сводим ее к / (t).

Если обозначить х = (t) х, то уравнение (13.52) разобьется на два:

Ti {t)xi + xi = f{t)-{t) T2it)xxi,

q>it)x-Ts{t)x, Ts{t)=Ti{t) a начальные условия будут

X = Хо, Xl = xio = Tz (0) Хо при

t = 0.

(13.53)

(13.54>

Формулы для решения уравнений (13.53) согласно [64, 78] будут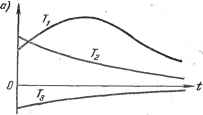

Ах At

1 Jt+At) TAt + At)

(13.55)

причем во второй из формул (13.55) значения Ах берутся со сдвигом на At!2 вправо по сравнению с Ах.

Отсюда вытекает следуюп,ее построение. Наносим заданные кривые Щ и (t), а также кривую Гд (t), ординаты которой определяются по второй из формул (13.54). Они показаны на графике (рис. 13.6, а).

На другом графике наносим заданное / (t) (рис. 13.6, б). На основании заданных начальных условий (см. выше) наносим на последнем графике точки Хо, и в середине первого интервала At (как в § 7.6) еще точку А с ординатой (7.76), т. е.

Рис. 13.6.

= Хо + -

-Хд.

Из точки El в середине первого интервала At на кривой / (t) откладываем вниз отрезок

(вниз, когда он положителен, и вверх, когда он отрицателен). При этом величина х берется как ордината уже имеющейся точки А, величина

Уз- берется из графика Т (t), а величина Xq - из заданных начальных