РАЗДЕЛ III

ОСОБЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 13

СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ § 13.1. Основные понятия

Линейными системами с переменными паражтрами называются системы, движение которых описывается линейными дифференциальными уравнениями с переменными во времени коэффициентами:

ao{t)

.+й 1 {t)~ + an {t)x--

.+bmi(t)J + bm{t)f{t). (13.1)

Коэффициенты о, . . ., a и &o, . . ., &m являются функциями времени, которые задаются либо графиками, построенными на основании эксперимента, либо аналитически.

Переменные коэффициенты в уравнении системы автоматического регулирования (13.1) возникают вследствие наличия переменных коэффициентов хотя бы в одном звене системы.

Так, например, у подвижного объекта (корабля, самолета, ракеты) с течением времени вследствие выгорания топлива проис- а) ходит изменение массы и моментов инерции. Если объект при своем движении меняет скорость и высоту, то возможно изменение его аэродинамических коэффициентов.

Рассмотрим переходную функцию и функцию веса системы с переменными параметрами. Так как коэффициенты уравнения (13.1) меняются с течением времени, то эти функции будут зависеть от момента прило- , жения единичного скачка или единичного импульса на входе. На рис. 13.1, а изображен график изменения одного из коэффициентов уравнения (13.1) и переходная функция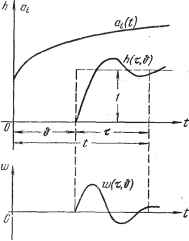

h{t - h (т, &),

(13.2)

Рис. 13.1.

где t - текущее время, отсчитываемое от некоторого момента, соответствующего, например, включению системы регулирования или началу изменения переменных параметров; & - время, соответствующее поступлению на вход единичной ступенчатой функции; т - текущее время, отсчитываемое от момента приложения ступенчатой функции.

Если теперь на вход подать единичную импульсную функцию, которую можно представить как предел отношения

Ав-О

ТО процесс па выходе, т. е. функцию веса, в силу принципа суперпозиции можно представить в виде разности двух смещенных на Дй переходных функций с измененным в l/Ad раз масштабом:

it Щ - lim t~ ]-М*-№+А). +Д]

Ав-0

Правая часть этого выражения представляет собой производную от переходной функции по аргументу &, взятую с обратным знаком. Таким образом, для функции веса получаем (рис. 13.1, б)

w(t - &, #) = w(t, &)= --fe (* &, &),

(13.3)

Как следует из (13.3), функция веса является функцией двух неременных: времени й, соответствующего моменту поступления на вход системы единичного импульса, и текущего времени t (или т = Z - ). В связи с этим функцию веса можно изобразить в виде некоторой поверхности (рис. 13.2).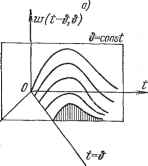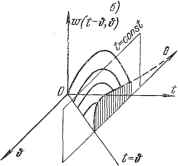

Рис. 13.2.

Эта поверхность переходит в плоскость tOb при < б. Границе перехода поверхности в плоскость соответствует биссектриса t = Это обстоятельство объясняется тем, что в реальных системах реакция не может появиться ранее приложения на входе системы импульса. Поэтому нри i < & функция веса должна быть тождественно равна нулю.

Сечение поверхности весовой функции вертикальной плоскостью, параллельной оси t (рис. 13.2, а), дает весовую функцию для фиксированного момента приложения единичного импульса на входе системы ( & = const). Эта функция называется нормальной весовой функцией системы с неременными параметрами:

w (i - &, &), & = const. (13.4)

Она является параметрической функцией, так как в нее входит фиксированный параметр Ь = const.

Нормальная весовая функция монет быть сделана зависящей от аргумента т - t - & подстановкой f = & + т. В результате получаем функцию

и; (т, &), & = const. (13.5)

§ IS.l]

ОСНОВНЫЕ понятия

Сечение поверхности весовой функции вертикальной плоскостью, параллельной оси &, дает кривую, образованную ординатами семейства нормальных весовых функций для фиксированного значения времени t = const (рис. 13.2, б). Эта кривая может быть получена путем обработки семейства нормальных весовых функций, построенных для различных моментов приложения единичного входного импульса & (рис. 13.3). Получающуюся зависимость будем называть сопряженной функцией веса: w{t- ,ffi w(t-&,&)

w {t - Щ, t = const.

(13.6)

Она также является параметрической функцией, так как содержит параметр t = const.

Сопряженная функция веса является функцией смещения но может быть представлена также как функция

аргзтиента Q = t - & (рис. 13.2, б;, называемого реверс-смещением, поскольку 6 отсчитывается от точки & = t в сторону, противоположную смещению Это осуществляется подстановкой в сопряженную весовую функцию значения Ь = t - 6 при t = const. В результате получаем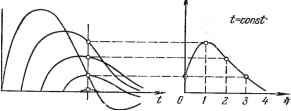

3 4

t=const

Рис. 13.3.

If (6, t - б), t = const.

(13.7)

Проиллюстрируем все сказанное примером. Пусть функция веса системы с переменными параметрами имеет вид

rv{t-<}, = -.

Зафиксировав смещение и положив, например, & = &о = const, получаем нормальную функцию веса:

ii;(i-&o, &о) = е о± или в другом виде, при переходе к аргументу т = t -

,-ат:

Ко)=-

Зафиксировав текущее время И положив, например, i = = const, получаем сопряженную функцию веса

Перейдя к реверс-смещению Q = t - &, имеем

Заметим, что в системах с постоянными параметрами весовая функция является функцией только времени т = i - & и не зависит от момента приложения & входного импульса. Рельеф функции веса (рис. 13.2) в этом случае получается цилиндрическим, а оба рассмотренных вьппе сечения (рис. 13.2, а и б) совпадают по форме и отличаются только знаками аргументов. При