изображенных, например, на рис. 12.16,12.19 и 12.21, для которых характерным является наличие участка с наклоном - 20 дб1деп в районе пересечения оси частот.

Различие будет наблюдаться в начальной части, если высокочастотная часть л. а. х. отличается от высокочастотной части л. а. х. типа 2-1-2, и в конечной части, если будут отличаться их низкочастотные части.

Таким образом, в случае нужды оценка переходных процессов может делаться по универсальным кривым, приведенным на рис. 12.22, во всяком случае для средней части кривой переходного процесса, которая показывает степень склонности системы к колебаниям.

В тех случаях, когда л. а. х. не имеет специального участка с наклоном - 20 дб/дек upvi переходе оси частот (см., например, рис. 12.18 и 12.20), оценка переходных процессов может быть сделана следующим образом..

t2 W 0.8 0,6

2 3 4

Рис. 12.23.

В кач:естве исходной примем л. а. х. типа 1-2 (рис. 12.18). Ей соответствует передаточная функция (12.102). Вводя единичное ступенчатое воздействие 01 (t), можно аналогично- изложенному выше построить нормированные переходные процессы в функции безразмерного времени (nt (рис. 12.23). Здесь в качестве coq принята частота пересечения асимптоты, имеющей наклон - 20 дб/дек, с осью частот (рис. 12.18).

Эти же кривые переходного процесса могут использоваться для оценки переходного процесса в случае использования л. а. х. другого типа, например 1-2-3 или О-1-2 (рис. 12.20). Как и в предыдущем случае, различие может наблюдаться только в начальной и конечной стадиях переходного процесса.

Построетше низкочастотной области желаемой п. а, х. Построение желаемой л. а. X. начинается с низкочастотной области. Из условий требуемой точности работы определяется положение контрольной точки или запретной области (см. рис. 12.11). Низкочастотная часть л. а. х. должна проходить не ниже контрольной точки или так, чтобы на заходить в запретную область.

В сиедящих системах с астатизмом второго порядка положение первой низкочастотной асимптоты, имеющей наклон 40 дб/дек, определяется совершенно однозначно. Из условий облегчения задачи демпфирования выгодно сдвигать эту асимптоту как можно более влево, т. е. в сторону низких частот. Очевидно, что предельное положение первой астштоты будет в том случае, когда она или пройдет через контрольную точку Аили сольется с правой границей запретной области (рис. 12.24).

Необходимое значение базовой частоты л. а. х. cuq и необходимый коэффициент усиления по разомкнутой цепи следящей системы определяются

ИЗ выражения (12.63):

©шах W

В следящих системах с астатизмом первого порядка необходимо определить положение двух первых асимптот, что можно сделать различным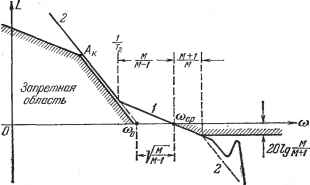

Рис. 12.24.

образом в зависимости от выбранного значения первой сопрягающей часто-ты со, = 1.

Если принять, что первая сопрягающая частота больше контрольной частоты со к не менее чем в 2-3 раза, то первые две асимптоты можно расположить так, чтобы через контрольную точку Л к прошла первая асимптота (рис. 12.25, а).

При этом коэффициент усиления по разомкнутой цепи или добротность по скорости Kq будет иметь минимальную возможную величину, равную предельному значению, определяемому из (12.62):

fil max

max L сек

ЧТО является благоприятным. Однако частота точки пересечения второй асимптоты с осью пуля децибел со о будет значительно больше минимального достижимого значения, определяемого по требуемому предельному коэффициенту усиления по ускорению (12.63). Это является нежелательным, так как вся л. а. х. будет сдвигаться в область более высоких частот, что затрудняет демпфирование вследствие относительного возрастания влияния всех постоянных р 25 времени системы.

Если теперь принять, что первая сопрягающая частота со, меньше контрольной частоты соц по крайней мере в 2-3 раза, то первые две асимптоты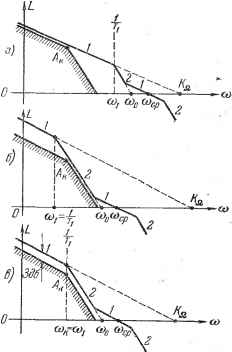

co ==-)/e = l/l/2-S5. (12.117)

Wi max

В статических следящих системах, а также в системах стабилизации построение низкочастотной части делается в соответствии с формулами (12.69)-(12.74).

Построение средне- и высокочастотной частей л. а. х. В системах с астатизмом второго порядка (рис. 12.24) необходимо осуществить типовой переход оси нуля децибел в соответствии с рис. 12.13. При этом известно значение базовой частоты сод.

Требуемое значение постоянной времени Т, определяется формулой (12.86).

Среднечастотной части л. а. х. соответствует асимптота с единичным лаклоном, проходящая в интервале амплитуд

или в интервале частот

- = co.p>co>co.pi. (12.118)

Часть л. а. х., лежащая правее частоты среза, может иметь, вообще говоря, произвольный вид, определяемый имеющимися в системе звеньями. Однако в соответствии с изложенным выше необходимо выполнение следующих условий.

1. Высокочастотная часть л. а. х. не должна заходить в запретную область, образованную асимптотой с единичным наклоном, пересекающей ось нуля децибел в точке со = соср, и горизонтальной прямой, соответствующей

. L(co) = 201g, . (12.119)

МОЖНО расположить так, чтобы через контрольную точку Л к прошла вторая асимптота (рис. 12.25, б). При этом частота пересечения второй асимптоты с осью нуля децибел ©о будет иметь минимальную возможную величину, определяемую предельным значением добротности по ускорению (12.63), что является благоприятным с точки зрения облегчения демпфирования системы. Однако при этом требуемый общ,ий коэффициент усиления по разомкнутой цепи Kq будет в 2-3 раза превышать минимальное возможное значение, определяемое формулой (12.62). Увеличение общ,его коэффициента усиления может неблагоприятным образом сказаться на возрастании влияния помех и наводок на входе. Поэтому выбор того или иного расположения низкочастотной части л. а. х. относительно контрольной точки должен определяться конкретными условиями.

При отсутствии преобладания того или иного фактора оптимальным следует считать такое расположение низкочастотных асимптот (рис. 12.25, в), при котором первая сопрягающая частота щ совпадает с контрольной частотой СОк-

Так как истинная л. а. х. в точке со == coj проходит ниже точки пересечения двух асимптот на 3 дб, или на 12, то вся л. а. х. при coi = со долнша быть поднята вверх на 3 дб. При этом требуемое значение коэффициента усиления

Zfi = V 2-sa, (12.116)

if max

Точке пересечения второй асимптоты с осью нуля децибел соответствует частота