лу (12.103). При значениях М, мало отличающихся от единицы, например при М 1,3, формула (12.105) является достаточно точной и может использоваться для расчета при наличии любого числа постоянных времени, а также при наличии временного запаздывания т, которое должно учитываться Б общей сумме постоянных времени.

Л. а. X. рассмотренного типа может использоваться в простейших следящих системах с невысокими требованиями в отношении статической и динамической точности. При невозможности удовлетворить требованиям технического задания приходится переходить к более сложным типам л. а. х. На рис. 12.19 изображена асимптотическая л. а. х. типа 1-2-1-2-3... Она может быть получена из соответствующей л. а. х. типа 2-1-2-3... системы с астатизмом второго порядка (рис. 12.16) добавлением одного излома при сопрягающей частоте 1

Этой л. а. X. соответствует передаточная функция разомкнутой системы

(12.106)

Так как обычно сопрягающая ча- Inc. 12.19.

стота (i>i значительно отличается от

частоты в зоне максимума требуемого запаса по фазе, то с большой степенью точности расчет можно вести по формулам, полученным в предыдущем параграфе для систем с астатизмом второго порядка. В этом случае положение л. а. X., изображенной на рис. 12.19, определяется базовой частотой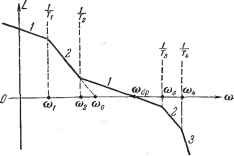

В соответствии с формулами (12.86) и (12.95) имеем

М -1

1 Ул/(м-1)

или в соответствии с формулами (12.88) и (12.96)

1 М т.п., .1

Tz>-

Л/ + 1

Шср М-1 Шср Л?4-1

Для уточнения расчета моншо учесть то обстоятельство, что по сравнению с системой, имеющей астатизм второго порядка, здесь имеется дополнительный запас по фазе

Afi = arctg(12.107)

Это позволяет немного увеличить допустимую сумму постоянных времени, которым соответствуют сопрягающие частоты правее частоты среза (формулы (12.95) и (12.96)), или немного уменьшить постоянную времени (формулы (12.86) и (12.88)). Однако подобное уточнение обычно не имеет практического значения [10] и почти всегда с достаточной степенью точности можно вести расчет параметров л. а. х. типа 1-2-1-2-3... по формулам, которые были получены для системы с астатизмом второго порядка (л. а. х. типа 2-1-2-3...).

Типовые л. а. х. статических систем. В простейшем случае передаточная функция разомкнутой статической системы имеет вид

(12.108)

где К - коэффициент усиления разомкнутой системы.

Соответствуюп];ая асимптотическая л. а. х. типа О-1-2 изображена на рис. 12.20.

В районе пересечения л. а. х. оси нуля децибел передаточная функция может бьсть приближенно сведена к передаточной функции системы с астатизмом первого порядка

W{p)-.

тде базовая частота л. а. х.

(Вп = -

(12.109)

(12.110)

Это дает возможность использовать полученную вьппе формулу (12.103) для л. а. X. типа 1-2 (рис. 12.18) при замене Kq на coq. Тогда моншо получить условие обеспечения заданного показателя колебательности

KTi ума-1

Го 2

Для передаточной функции более сложного вида аналогично (12.105) имеем

\ Л/Г9. I Л/Г Т / Л/7Й а

(М<1,3).

(у1 + у2+---) М--МУм - ! То -2

(12.111)

(12.112)

(12.113)

Из этих формул ВИДНО значение первой большой постоянной времени чкак фактора, увеличиваюп];его запас устойчивости системы. Повьппение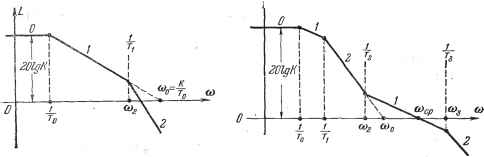

Рис. 12.20.

Рис. 12.21.

коэффициента усиления или повышение суммы остальных постоянных времени при заданном показателе колебательности может быть сделано нри одновременном увеличении постоянной времени Т-

Отклонение передаточной функции (12.109) от более точного выражения (12.108) в области низких частот дает некоторое увеличение запаса устойчивости, т. е. уменьшение колебательности. Учет этого обстоятельства обычно нецелесообразен ввиду незначительности получаемого эффекта [10].

При повышенных требованиях по статической и динамической точности аюгут применяться л. а. х. типа 0-1-2-1-2-3... (рис. 12.21), образован-

ные из л. а. х. типа 2-1-2-3... (рис. 12.13) систем с астатизмом второго порядка.

iaKHM л. а. х. соответствует передаточная функция разомкнутой системы

W{p)-

(12.114)

Как и в случае систем с астатизмом перного порядка, здесь можно с достаточной степенью точности пользоваться универсальными формулами (12.86)- (12.89) и (12.95), (12.96).

Учет звеньев постоянного запаздывания и колебательных звеньев, а также введение границы малых постоянных времени может делаться аналогично изложенному выше.

Переходные процессы, соответствующие типовым л. а. х. Для л. а. х. типа 2-1-2 моншо показать, что при заданной протяженности h асимптоты с единичным наклоном (рис. 12.13) выбор параметров, при котором обеспечивается минимальное значение показателя колебательности (12.83), вместе с тем соответствует некоторому оптимальному протеканию переходных процессов. При этом будет иметь место максимальное приближение кривой переходного процесса к некоторой экстремали, которая является экспонентной с постоянной времени Т = а>о%-\

Чем больше протяженность участка h, тем меньше показатель колебательности и тем более благоприятным будет протекание переходного процесса, так как постоянная времени экспоненты будет меньше.

Определим вид переходного процесса при единичном входном воздействии = 1 {t) для случая использования л. а. х. типа 2-1-2 (рис. 12.13).

Для нормированной передаточной функции (12.77) изображение Лапласа выходной величины будет.иметь вид

Рис. 12.22.

T3g3-i-g2+T2ff-i-l q

(12.115)

Таблица 12.7 Параметры переходных процессов

Задаваясь различными значениями показателя колебательности, можно найти относительные постоянные времени = cOoTg и = ЮоГд и затем

построить переходный процесс для выходной величины Og в функции безразмерного времени Mq*. Переходные характеристики показаны на рис. 12.22.

Параметры переходных процессов - перерегулирование о% и относительное время переходного процесса о*п - для i 1 - ( оО I < 0,05 приведены в табл. 12.7.

Хотя эти кривые переходных процессов соответствуют л. а. х. типа 2-1-2 системы с астатизмом второго порядка (рис. 12.13), они с большой степенью точности могут использоваться для оценки переходных процессов при использовании л. а. х. других типов.