то эта постоянная может не учитываться при расчете.

Расчетная формула для определения допустимого значения постоянной времени (12.86) при этом сохраняется, а вместо формулы (12.87) должно использоваться выражение

<~{ЩОЛ). (12.93)

В более сложном случае передаточная функция разомкнутой системы может иметь произвольное число постоянных времени, входящих в ее знаменатель:

(/)= ра+т,рн1+п1п1+тр) ... (12.94)

-Этой передаточной функции соответствует л. а. х. типа 2-1-2-3-4...

Расчеты и здесь оказываются достаточно простыми. Для получения заданного показателя колебательности необходимо вьшолнение условия (12.86) для постоянной времени Т- Сумма всех остальных постоянных времени 27 = Гз + -f -f . . ., включая малые постоянные времени, должна удовлетворять неравенству

При использовании расчета по частоте среза для постоянной времени 72 должно выполняться условие (12.88), а для суммы остальных постоянных времени - условие

Т<- (12.96)

В л. а. X. подобного типа легко учесть наличие звеньев постоянного запаздывания ). В этом случае время запаздывания т должно учитываться при подсчете суммы постоянных времени 2 Г.

Возможен случай, когда в передаточную функцию разомкнутой системы входит множитель, соответствующий колебательному звену с комплексными корнями:

Допустить наличие такого множителя можно в том случае, если частота свободных колебаний звена значительно больше базовой частоты:

до = > )о. . (12.98)

Асимптотическая л. а. х. для этого случая изображена на рис. 12.16.

1) О звеньях постоянного запазныюния см. главу 14.

а число малых постоянных времени принимать равным 46. Тогда граница малых постоянных времени определяется значением

Г = ?м 0 (12.91)

Если некоторая постоянная времени дает сопрягающую частоту <Вм = которая больше граничной частоты (рис. 12.15)

С0г = = 400)0, (12.92)

При выполнении условия (12.98) фазовый сдвиг, вносимый колебательным звеном Б районе максимального запаса по фазе, можно принять равньш arctg а (В. Поэтому коэффициент а должен входить в общую сумму постоянных времени (12.95) или (12.96).

Для того чтобы избежать появления второй запретной зоны в районе пика л. а. х. при а> тд (рис. 12.16), необходимо выполнение дополнительного условия, которое вытекает из неравенства (8.87):

moAW{jqo) = A{qo)<-. . (12.99)

Вьшолнение этого условия может быть легко проверено при построении л.а.х.

Более подробно этот вопрос рассмотрен для случая гироскопических следящих систем в [10].

Предельным случаем л. а. х. типа 2-1-2 или типа 2-1-2-3 является л. а. X. типа 2-1 (рис. 12.17), соответствующая случаю, когда 2Г0.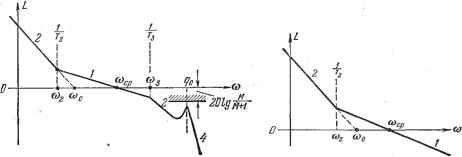

Рис. 12.16.

Рис. 12.17.

Тогда передаточная функция разомкнутой системы (12.94) приобретает вид

Щ{р) =

(12.100)

Передаточная функция подобного вида соответствует изодромному регулированию. Она может встречаться, например, в сглаживающих системах различного типа, построенных на электромеханических, электронных, гироскопических и тому подобных интеграторах.

Показатель колебательности для подобной передаточной функции может быть определен прямым отысканием максимума модуля частотной передаточной функции замкнутой системы

W (/со)

1+Т(/ш)

= М.

Подстановка (12.100) и исследование получившегося выражения на максимум дает следующее условие, которое должно быть выполнено, чтобы показатель колебательности не превьппал заданного значения:

или, в другом виде (при условии, что > СОо),

2 т-М

Tz>

(12.101)

Типовые п. а. х. систем с астатизмом первого порядка. Следящие системы с астатизмом первого порядка представляют собой наиболее

распространенный тип систем, содержащих одно интегрирующее звено - исполнительный двигатель. В простейшем случае, когда следящая система состоит из безынерционного усилителя и исполнительного двигателя с постоянной времени и не имеет дополнительных корректирующих средств, кроме, возможно, жесткой тахометрической обратной связи, передаточная функция разомкнутой системы может быть сведена к виду

W{p)-

7(iW (12.102)

Астштотическая л. а. х. типа 1-2, соответствующая этой передаточной функции, изображена на рис. 12.18.

Определение допустимого значения постоянной времени может быть сделано прямым нахождением максимума амплитудной частотной характеристики замкнутой системы

W (/со)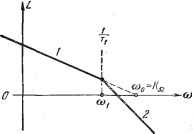

= м-.

Подставляя (12.102) и исследуя получившееся выражение па максимум, можно найти условие того, чтобы показатель колебательности не превышал заданного значения:

ад< +% (12.103)

Рис. 12.18.

Последняя формула позволяет при заданном значении постоянной времени исполнительного двигателя легко определять максимальное значение добротности по скорости, которое можно иметь в следящей системе при данном значении показателя колебательности.

При заданном значении требуемой добротности по скорости эта же формула позволяет определять допустимое значение постоянной времени исполнительного двигателя и необходимый коэффициент усиления по петле жесткой тахометрической обратной связи, служащей для снижения постоянной времени двигателя. Определение коэффициента усиления для тахометрической обратной связи может производиться по формуле

1 + Лос

где Гд - постоянная времени исполнительного двигателя, кос - коэффициент усиления по петле тахометрической обратной связи.

В более сложном случае передаточная функция (12.102) может быть представлена в виде

W{p):

(12.104)

>(1+ад (1-I-зд (1+3?).

Этой функции соответствует л. а. х. типа 1-2-3-4...

Здесь может быть получена приближенная формула, ориентировочно связывающая сумму всех постоянных времени с добротностью по скорости:

(12.105)

при М < 1,3.

Приближенная формула (12.105) становится точной при Af = 1 и любом числе постоянных времени либо при наличии только одной постоянной времени и любом значении М. В последнем случае она вырождается в форму-