малы. Показатель колебательности М = 1,3 -+ 1,5 обычно является вполне достаточным для большинства следяш;их систем. Во многих случаях следящие системы работают удовлетворительно и при значениях М = 1,6 1,8.

Необходимым и достаточным условием того, чтобы в устойчивой системе показатель колебательности был не больше заданного, является нахождение фазовой характеристики вне запретной зоны (рис. 8.27). В минимально-фазовых системах это условие может быть выдержано соблюдением определенных правил построения л. а. х. без нахо/кдения фазовой характеристики.

Рассмотрим принципы построения л. а. х. с заданньш показателем колебательности. По методическим сообранениям рассмотрение начнем со следящих систем с астатизмом второго порядка, хотя эти системы и не относятся к наиболее простым и распространенным.

Как правило, в качестве типовых используются л. а. х., имеющие в низкочастотной части наклон не более 40 дб18ек. Это вызвано стремлением избавиться от условий, при которых возможно появление неустойчивости в большом, т. е. при согласовании следящей системы с большого угла.

Типовые л. а. х. систем с астатизмом второго порядка. В системах с астатизмом второго порядка обьгано имеются два интегрирующих звена. Такими звеньями могут быть исполнительный и вспомогательный двигатели, например гидромуфта и управляющий двигатель, поворачивающий пшин-дель или чашу гидронасоса. В некоторых случаях астатизм второго порядка может появляться вследствие особенностей механических характеристик единственного исполнительного двигателя, у которого вращающий момент не зависит от скорости вращения.

Рассмотрим передаточную функцию разомкнутой системы вида

W{p)-.

(12.75)

где Ке

Г 1 1

- коэффициент усиления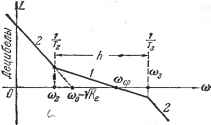

по разомкнутой цепи, назьшаемый до- Рис. 12.13.

бротностью по ускорению.

Асимптотическая л. а. х., соответствующая (12.75), изображена на рис. 12.13. В соответствии с наклонами асимптот, кратными - 20 дб1дек, ей присвоен тип 2-1--2.

Положение всей л. а. х. может быть задано точкой пересечения первой асимптоты с осью нуля децибел. Этой точке соответствует частота

0)o = l/Ze,

(12.76)

которую назовем базовой.

При введении новой переменной q = - передаточная функция будет представлена в нормированном виде:

(12.77)

где = 0)02 и Tg = (Bos - относительные постоянные времени.

Соответствующая нормированная л. а. х., построенная для относительной частоты у = -, изображена на рис. 12.14. Здесь же показаны для

иллюстрации фазовая характеристика и запретная область для нее.

Протяженность участка с единичным наклоном, т. е. с отрицательным наклоном 20 дб/дек = 6 дб/окт, определяется отношением двух постоянных

времени:

(12.78)

Под протяженностью участка вдоль оси частот (рис. 12.14) понимается тношепие частот конечных точек участка (большей к меньшей). Запас по фазе для функции (12.77)

р, = arctg 1/Т2 - arctg 1/Т3 = arctg

Исследование на максимум дает

1/м = -

Ртах = arctg

fe -1

(12.79)

(12.80) (12.81)

Максимальный запас по фазе определяется только протяженностью h асимптоты л. а. х., тлеющей, единичный наклон.

Приравнивание максимальных запасов по фазе (8.88) и (12.81) дает зависимость между протяженностью участка h и показателем колебательности М при оптимальном выборе параметров, т. е. при совпадении максимумов реальной фазовой характеристики и запретной зоны (рис. 12.14):

М-1-1

-ш,о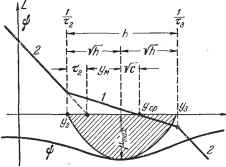

M - i

(12.82) (12.83)

Рис. 12.14.

Эти формулы связывают протяженность участка h с минимальным значением показателя колебательности, который может быть получен при этой протяженности, или величину показателя колебательности М с минимальной протяженностью участка h, обес-печиваюп];ей этот показатель колебательности.

Из рис. 12.14 легко найти оптимальные параметры л. а. х.:

rW5= §±i/-/s. (12.84,

где j/C соответствует модулю, а 1/]/С- относительной частоте, нри которых запас по фазе (в запретной области) получается максимальным (ом. формулу (8.88));

Та УМ(М -1)

(12.85)

Эти параметры соответствуют минимальному значению показателя колебательности при заданной протяженности участка h.

Следует заметить, что технически реализовать систему тем легче, чем меньше протяженность участка h. Это связано с необходимостью подъема па этом участке верхних частот, что во многих случаях затруднено вследствие наличия в системе внешних и внутренних высокочастотных помех. Поэтому с точки зрения оптимальности инженерного решения необходимо

стремиться к реализации нелаемых динамических качеств при минимальной требуемой протяженности участка h.

Для получения заданного показателя колебательности в замкнутой системе при фиксированной базовой частоте л. а. х. необходимо иметь следующие постоянные времени:

1 м

1 Ум {M-i)

(12.86) (12.87)

Вместо базовой частоты ©о за точку, фиксирующую положение л. а. х. (рис. 12.13 и 12.14), можно принять, например, точку пересечения второй асимптоты л. а. х. с осью децибел, которой соответствует частота = (Hoi-Тогда вместо (12.86) и (12.87) получим выражения, которые при фиксированной частоте среза, а следовательно, и фиксированном положении запретной зоны для фазовой характеристики можно превратить в неравенства:

cocpi М+1

(12.88) (12.89)

При равенстве левых частей правым показатель колебательности будет равен заданному значению М. При неравенстве левых и правых частей будет вводиться некоторый дополнительный запас устойчивости и показатель колебательности будет снижаться.

Эти формулы легко запоминаются, и они просто связаны с параметрами окружности - запретной зоны на комплексной плоскости (см. рис. 8.28).

В неравенство может быть превращена и формула (12.87). Формулу (12.86) лучше иметь Б виде равенства, так как увеличение Tz по сравнению с тем, что дает формула, в некоторых случаях меняет привести к ухудшению запаса устойчивости.

При использовании типовой передаточной функции (12.75) может быть предусмотрен дополнительный запас устойчивости для возможности иметь в усилительном канале некоторое количество не учитываемых при расчете малых постоянных времени. Дополнительный запас устойчивости создается уменьшением величины постоянной времени Т или, соответственно,

тобы отодвинуть фазовую характеристику от запретной области (рис. 12.15).

На малые постоянные времени отводится обьгано несколько градусов запаса по фазе. Так, например, в [10] предлагается отводить на эти цели величину, соответствующую сумме малых постоянных,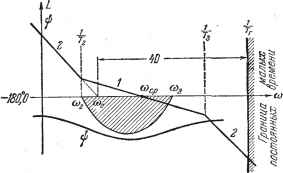

Рис. 12.15.

2Гм =

(12.90)