В табл. 12.5 приведены некоторые типовые значения Рщах и соответствующие им качественные показатели замкнутой системы.

Таблица 12.5

После нахождения основных величин для тиловой вещественной характеристики переходят к формированию желаемой логарифмической амплитудной характеристики. При этом очевидно, что фазовая характеристика разомкнутой системы должна так проходить, чтобы обеспечивалась не только устойчивость, но и определенный запас устойчивости.

Запас по фазе 60°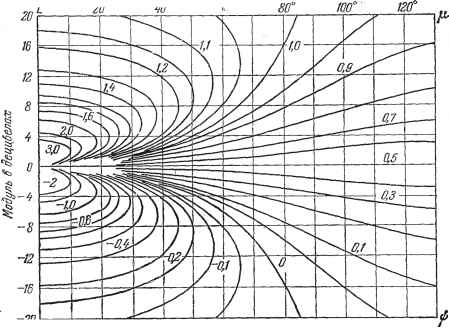

-т° -Ж -ЮО

Фазобый сдвиг Рис. 12.7.

-80° -60°

Вещественная характеристика замкнутой системы связана с частотной передаточной функцией разомкнутой системы W (]а>) зависимостью

РМ-Вс Ее

(12.49)

Задаваясь различными значениями Р (со) = const, на комплексной плоскости можно построить кривые, дающие связь между вещественной и мнимой частями W (/со) или между ее модулем и фазой (или запасом по фазе). На рис. 12.7 приведено подобное семейство кривых для амплитуды.

12.5]

МЕТОД ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК

60°

40°

Откладываемой в децибелах. Цифры около соответствующих кривых указывают значение Р (ш). Если на этом графике нанести амплитудно-фазовую характеристику системы, то по точкам пересечения с кривыми можно построить вещественную характеристику.

Кривые, приведенные на рис. 12.7, позволяют сформулировать требования к амплитудно-фазовой характеристике разомкнутой системы, которые необходимо выполнить, чтобы обеспечить получение желаемой типовой характеристики.

Так, например, если необходимо, чтобы о%30%, то максимальная и минимальная ординаты вещественной характеристики в соответствии с табл. 12.5 не должны превьппать значений (ориентировочно) -Ртах Ij и I Ртп1ъ I 0,2. Это означает, что логарифмическая амплитудно-фазовая характеристика, нанесенная на рис. 12.7, не должна ваходить в области, ограниченные кривыми с отметками 1,2 и 0,2. Сформулированное условие будет выполняться, если амплитудно-фазовая характеристика не будет заходить в прямоугольник, образованный горизонтальными линиями = = 16 дб ж Lz = -16 дб ж вертикальной линией я]) = -135° (или в величинах запаса по фазе р, = 180° -Ь я]; = 45°).

В соответствии с этим на рис. 12.8 построены кривые, которые позволяют при заданном значении перерегулирования выбирать требуемое значение запаса по модулю = \ \ ж запаса по фазе ц..

Рис. 12.8.

40 6%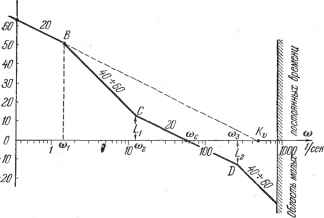

Риса 12.9.

Построение желаемой асимптотической л. а. х. производится в следующем порядке.

Первая низкочастотная асимптота проводится так, чтобы она имела наклон - 20 дб1дек, соответствующий астатизму первого порядка (рис. 12.9). Продолжение асимптоты должно пересечь ось частот при частоте, равной желаемой добротности по скорости:

К.=-, (12.50)

где Cj - заданный коэффициент опеибки.

При однократном изломе в точке В первая сопрягающая частота определяется по формуле

(12.51)

где =--добротность системы по ускорению, а при двукратном изло-

-2 ,

ме - по формуле

(12.52)

Далее по найденной из рис. 12.6 частоте положительности и определяется частота среза л. а. х. ср так, чтобы она удовлетворяла условию

<йср = (0,6 0,9) п- (12.53)

Среднечастотный участок желаемой л. а. х. образуется асимптотой с наклоном - 20 дб1дек, проводимой так, чтобы она пересекала ось частот при (йср- Этот участок проводится влево и вправо до достижения модулей, равных и Lg (рис. 12.9). Затем производится сопряжение среднечастотного участка с низкочастотными асимптотами и высокочастотной частью.

Для облегчения построения желаемой л. а. х. вводятся типовые передаточные функции и им соответствующие л. а. х. Они даны в табл. 12.6.

Таблица 12.6 Типовые передаточные функции и л. а. х.

Тип л. а. X.

II III IV

Передаточная функция

р(1 + ад (l-bTsP)

р(1 + г1р)(1-ЬГзРР -К(1 + Т2рЯ

Отрицательные наклоны асимптот в дб/дек

20-40-20-40 20-60-20-40 20-40-20-60 20-60-20-60

Передаточные функции и л. а. х. всех четырех типов полностью определяются заданием четырех величин: коэффициента усиления К и трех

11 1

сопрягающих частот (й = -, = - и Юд = - (рис. 12.10). л. а. х.

1 Т2 3

полностью определяется также заданием следующих четырех величин: коэффициента усиления в децибелах при частоте ю = coi, частоты среза соср

и двух относительных сопрягающих частот - и

ср ср

к малым параметрам (рис. 12.9) относятся те постоянные времени систе- мы, пренебрежение влиянием которых не сказывается существенно на динамических качествах системы. Обычно считают, что в качестве малых постоянных времени можно принять такие, которые удовлетворяют условию

<(53)1 (12.54)

При построении желаемой л. а. х. нужно следить, чтобы она как можно меньпю отличалась от располагаемой л. а. х., что нужно для упрощения