в этом случае безразмерные коэффициенты А, . . ., An-i являются коэффщиентами бинома Ньютона.

Однако переходный процесс затухает быстрее, если характеристическое уравнение при четном п имеет вид

(12.44)

и при нечетном п

{р + Оо){р + 2Щор + Ю =0.

(12.45)

причем безразмерный параметр затухания = 0,7 -- 0,8.

В табл. 12.3 для случая t, = 0,75 приведены значения безразмерных коэффициентов А, . . ., причем Ло = 1 и Л = 1, для степени харак-

теристического уравнения от 2 до 6.

Таблица 12.3

Коэффициенты характеристического уравнения для кратных корней

На рис. 12.4, в приведены нормированные переходные характеристики, соответствующие характеристическому уравнению (12.45), если в него ввести правую часть в виде fi / (t).

Переходный процесс затухает еще быстрее, если принять некратное распределение комплексных корней [61]. В этом случае все корни имеют одинаковую вещественную часть т]. Мнимые части корней образуют арифметическую прогрессию с разностью у и первым членом также у. Для каждой степени характеристического уравнения существует некоторое оптимальное отнощение y/iq, которому соответствует наибольщее быстродействие в безразмерном времени. Безразмерные коэффициенты характеристического уравнения для этого случая приведены в табл. 12.4, а переходные характеристики изображены на рис. 12.4, г.

Таблица 12.4 Коэффициенты характеристического уравнения (оптимальный случай)

При наличии нулей у передаточной функции принятые в табл. 12.3 и 12.4 распределения корней оказываются неудачными вследствие появления больпюго перерегулирования. В зтом случае оказывается более выгодным использование расположения корней па вещественной оси по арифметической прогрессии (см. табл. 12.1 и 12.2).

§ 12.5. Метод логарифмических амплитудных характеристик

Наиболее приемлемы для целей синтеза логарифмические амплитудные характеристики, так как построение л. а. х., как правило, может делаться почти без вычислительной работы. Особенно удобно использовать асимптотические л. а. X.

Процесс синтеза обычно включает в себя следующие операции.

1. Построение желаемой л. а. х. Построение желаемой л. а. X. делается на основе тех требований, которые предъявляются к проектируемой системе регулирования. При построении желаемой л. а. х. необходимо быть уверенным, что вид амплитудной характеристики полностью определяет характер переходных процессов и пет необходимости вводить в рассмотрение фазовую характеристику. Это будет выполняться в случае минимально-фазовых систем. В этом случае амплитудная характеристика однозначно определяет вид фазовой характеристики. Напомним, что передаточная функция разомкнутой минимально-фазовой системы не должна иметь пулей и полюсов, расположенных в правой полуплоскости (см. § 4.8).

2. Построение располагаемой л. а. х. Под располагаемой л. а. X. понимается характеристика исходной системы регулирования, построенной исходя из требуемых режимов стабилизации или слежения, требуемых выходной мощности, скорости, ускорения и т. п. Обычно под исходной системой понимается система, состоящая из регулируемого объекта и регулятора и не снабженная необходимыми корректирующими средствами, обеспечивающрши требуемое качество переходного процесса. Исходная система должна быть также минимально-фазовой.

3. Определение вида и параметров корректирующего устройства. Наиболее просто определяется корректирующее устройство последовательного типа. Если желаемая передаточная функция разомкнутой системы - W,k (j>), располагаемая - Ир (р) и передаточная функция корректирующего звена последовательного типа - Wns (р)) то можно записать равенство

Иш(р) = Ир(р)Ипэ(р), (12.46)

откуда

-() = - (2.47) Для л. а. X. можно записать

пз (со) = L (сй) - Lp (сй). (12.48)

Таким образом, при использовании л. а. х. весьма легко осуществляется синтез последовательных корректирующих средств, так как л. а. х. корректирующих средств получается простым вычитанием ординат располагаемой л. а. X. из ординат желаемой.

4. Техническая реализация корректирующих средств. По виду л. а. х. необходимо подобрать схему и параметры корректирующего звена последовательного типа. В случае необходимости последовательное звено может быть пересчитано на эквивалентное параллельное звено или эквивалентную обратную связь по формулам, которые приведены в § 10.4.

5. Поверочный расчет и построение переходного процесса. В случае необходимости полученная система регулирования вместе с корректирующими средствами может быть исследована обычными методами анализа.

Ниже приводится краткое изложение метода синтеза, разработанного В. В. Солодовниковым [121] для следящих систем с астатизмом первого порядка.

В основу синтеза положены следующие показатели качества:

1) перерегулирование о% при единичном ступенчатом воздействии на входе;

2) время переходного процесса

3) коэффициенты ошибок и

в рассмотрение вводится типовая вещественная частотная характеристика замкнутой системы (рис. 12.5). Эта характеристика описывается сле-

дующими

4>fl у у W/r

величинами: = - основной коэффициент наклона; а = -

и 1 = - - дополнительные коэффициенты наклона; Х = ж%. - -

основной и дополнительный коэффициенты формы; cOjj - интервал положительности.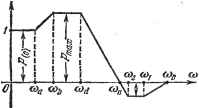

60 40 30 20 10

Рис. 12.5.

1.0 1,1 12 13 ф tJ5 Ртах

Рис. 12.6.

Если в следящей системе с приемлемыми динамическими качествами для вещественной частотной характеристики выполняются условия:

0,8, Иа>0,4, ?>0,5,

то, как показало построение соответствующих типовых вещественных характеристик переходных процессов, величина перерегулирования в основном определяется величиной Рщах- В этом случае перерегулирование о % и время переходного процесса могут быть определены по кривым, приведенным на рис. 12.6.

Таким образом, на основании заданного перерегулирования о% можно определить Ртах и затем по Рщах зависимость между временем переходного процесса t-u и частотой сОд, соответствующей интервалу положительности вещественной характеристики. По заданному значению легко определяется требуемое значение со д. ц

Однако отрицательная часть вещественной характеристики также влияет на перерегулирование, увеличивая его на величину До 0,3 Рт-Это можно учесть, положив Рт - -Ртах- Тогда по кривой, изображенной на рис. 12.6, можно найти допустимые значения Ртах и Ртш = = 1 - Ртах при которых Суммарное перерегулирование не будет превосходить заданного значения о %.