Ф2 + Фз = -2--

Рассматривая график на рис. 12.2, можно заметить, что

= Фз + Р, -- + а = ф2.

откуда следует, что а р. Это равенство и представляет собой условие для -определения точки пересечения В.

6. Направление касательной к траектории при выходе ее из какого-либо полюса или при подходе к какому-либо пулю нетрудно определить путем вычисления угла между этой касательной в данном полюсе или нуле и вещественной осью. При таком вычислении используется зависимость (12.38)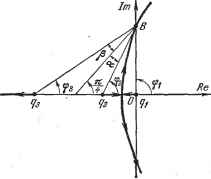

Рис. 12.2.

Рис. 12.3.

для аргументов всех пулей и полюсов, расположенных по условию в левой полуплоскости комплексной переменной р.

На рис. 12.3 изображены траектории корней передаточной функции G (р), имеющей два нуля и два полюса па вещественной оси и одну пару комплексных сопрян?енных полюсов. При достаточно малом удалении точки р от полюса углы ф5, ф , фц ф2 и фд, соответствующие остальным пулям и полюсам, останутся неизменными. Таким образом, в силу (12.38) угол ф найдется из уравнения

(ф? + ф ) - (ф1 + Фг + Фз + ф4) = я.

Перечисленные правила определяют основные свойства траекторий корней. Траектории вне нулей и полюсов функции G (р) находятся с помощью построения по точкам, после чего можно определить характер изменения К вдоль построенной таким образом кривой. После того как выбрано желаемое расположение корней характеристического уравнения, находится соответствующее значение К. Более подробно см. [128].

§ 12.4. Метод стандартных переходных характеристик

Для получения необходимых значений коэффициентов передаточной функции разомкнутой системы можно воспользоваться стандартными переходными характеристиками. Для большей общности эти характеристики строятся в нормированном виде. В этом случае по оси времени откладывается относительное время т = Qt, где - среднегеометрический корень характеристического уравнения, определяющий быстродействие системы.

При построении стандартных переходных характеристик необходимо задаться определенным распределением корней характеристического уравнения.

Ниже приводятся стандартные характеристики и соответствующие передаточные функции [61].

Для систем с астатизмом первого порядка корни приняты веществен-ньши, причем они составляют арифметическую прогрессию. В табл. 12.1

Таблица 12.1

Стандартные передаточные функции разомкнутой системы с астатизмом первого порядка при n = 2~i

приведены передаточные функции разомкнутой системы для различных порядков характеристического уравнения к - 2 +- 4, получающиеся при этом значения перерегулирования а% и добротности по скорости К .

Нормированные переходные характеристики для канедого случая приведены на рис. 12.4, а.

Для систем с астатизмом второго порядка корни также приняты вещественными, причем они составляют геометрическую прогрессию. Соответствующие передаточные функции приведены в табл. 12.2, а переходные характеристики - на рис. 12.4, 6.

Таблица 12.2

Стандартные передаточные функции разомкнутой системы с астатизмом второго порядка при г=2н-6

В табл. 12.2 для различных порядков характеристического уравнения и = 2 6 приведены передаточные функции разомкнутой системы, перерегулирование 0% и добротность по ускорению Кв.

Использование метода стандартных переходных характеристик для синтеза заключается в том, что для принятой структурной схемы выбирается приемлемый вид переходного процесса. Это позволяет установить необходимое значение среднегеометрического корня Q. Далее оказываются известными все коэффициенты желаемой передаточной функции системы. Введением различных корректирующих средств необходимо добиться того, чтобы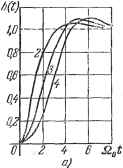

2 4

8 Ю S2 t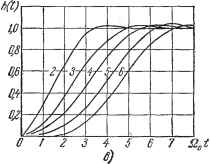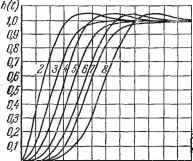

0 1 2 3 4 5 6 7 8 S 10 11 Slgt Рис 12.4.

коэффициенты реальной передаточной функции были возможно ближе к коэффициентам желаемой передаточной функции.

Этот метод может применяться и в том случае, когда важно обеспечить требуемую точность работы системы, которая может быть задана, например, при помощи коэффициентов ошибок. Тогда при заданных значениях коэффициентов ошибок можно определить требуемое значение К и или К, а по ним найти величину О:. Далее расчет ведется так, как описано выше.

Недостатком рассмотренного метода является то, что при построении стандартных переходных процессов приняты вещественные корпи. Это во многих случаях не приводит к оптимальному решению. Однако стандартные переходные характеристики можно сравнительно просто построить для любого другого расположения корней, в том числе и для комплексных корней. Предлагается, например, такое решение [61]. Пусть характеристическое уравнение записано в виде

+ ЛйоР - + 2оР - + . . . + fi? = О, где - среднегеометрический корень.

Если принять все корпи равными и вещественными, то это характеристическое уравнение приобретает вид

(р + fi ) = 0. (12.43)