§ 2.2]

ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ЗАКОНЫ РЕГУЛИРОВАНИЯ

что расп1иряет возможности целесообразного изменения качества процесса регулирования.

Примеры динамических нелинейностей в законе регулирования:

и - к {I ± b \ X \) X, и = к {I ± b \ X \) X, и = к {I ± \ и \) X,

утройстдо

Усилитель-

где вместо двойного знака подразумевается какой-либо один из них.

Подобные динамические члены нелинейного закона регулирования различно влияют на демпфирующие свойства системы регулирования в переходных процессах в зависимости от размеров и скорости отклонения. Они же могут существенно улучгаать динамическую точность (т. е. умень-гаать динамические огаиб-ки) системы в различных режимах вынужденного движения, воспроизведения различных форм зада-ваемых входных сигналов, а также при случайных воздействиях.

Отметим, что функциональные нелинейные за- Рис. 2.7. коны регулирования могут быть связаны не только с изменением параметров в зависимости от размеров входных воздействий, но и с изменением структуры. Например, при увеличении отклонения регулируемой величины сверх определенного порога I а; I = с в системе может происходить переключение с одного линейного корректирующего устройства на другое.

Логические нелинейные законы регулирования. Нелинейные законы регулирования могут иметь иные формы, которые

реализуются с помощью не функциональных, а более или менее сложных логических устройств. Будем называть их логическими нелинейными законами регулирования.

Например, в системе на рис. 2.7 логический нелинейный закон регулирования может быть применен для экономии управляющих воздействий со стороны регулятора на объект (а также экономии расхода энергии на нужды регулирования).

Построение простейгаего логического нелинейного закона регулирования лучгае всего пояснить на плоскости двух входных величин и, и (рис. 2.8). Последние с точностью до характеристик неидеальности измерила;

телеи соответствуют отклонению х и скорости отклонения регулируемой величины (рис. 2.7).

Предварительно заметим, что если знак скорости совпадает со знаком отклонения х, то величина отклонения х по модулю возрастает. В этом случае требуется энергичное действие регулятора для его ликвидации.

Если же знак скорости противоположен знаку отклонения х, то величина ] X I уменыаается. В этом случае можно вовсе не подавать на объект

Рис. 2.8.

управляющего воздействия, если скорость достаточна для необходимой

быстроты ликвидации отклонения, или же подавать воздействие при-очень

малой скорости , Эти рассуждения позволяют считать целесообразным,

например, применение следующего логического закона регулирования.

Управляющее воздействие (ug = +1 или = -1) включается только тогда, когда > и* (см. рис. 2.8), т. е., когда отклонение достаточно велико и U2 имеет знак, одинаковый со знаком щ или противоположный, но при малом I 2 I < Uz- Во всех остальных случаях управление вьшлюче-но (ug = 0), так как при противоположных знаках щ ш щ и достаточной величине \щ \ > система] сама, без управления возвращается к требуемому положению X = О (если при этом гарантирована противоположность

знаков и х). Более подробно эта система будет рассмотрена в разделе IV.

Логические нелинейные законы регулирования могут быть связаны также с изменением структуры системы регулирования. Например, при помощи логического устройства можно включать и выключать сигналы управления по первой и второй производным и по интегралу, в зависимости от сочетания значений отклонения регулируемой величины х и скорости

отклонения ее . Если правильно сформировать логику этих переключений,

то можно существенно повысить качество работы системы регулирования.

Вместо комбинирования указанных линейных членов закона регулирования могут вводиться также и функциональные нелинейные члены; включение и выключение сигналов, соответствующих этим членам, производится при помощи логического устройства. Тогда получится комбинация функциональных и логических нелинейных законов регулирования.

Оптимизирующие нелинейные законы регулирования. В настоящее время интенсивно развивается теория оптимальных процессов регулирования. При этом на основе классических вариационных методов, или на основе так называемого принципа максимума, или методом динамического программирования определяется закон регулирования таким образом, чтобы система имела максимум быстродействия, или минимум ошибки, или же минимум какой-нибудь другой величины (в форме функционала) с учетом ограничений, накладываемых в реальной системе на координаты, скорости, силы и т. п.

Как правило, при этом приходят к нелинейным законам регулирования, хотя, вообще говоря, можно оптимизировать и коэффициенты линейного закона, задав его форму. Часто оптимальный нелинейный закон регулирования состоит в переключении управляющего воздействия (при определенных состояниях системы) с одного максимально возможного значения на другое (противоположного знака). Моменты переключения в целом определяются сложными комбинациями значений нескольких переменных и их производных.

Параметрические нелинейные законы регулирования. В предыдущих типах законов регулирования вводились отклонения регулируемой величины от некоторых заданных ее программных значений. При параметрической программе управления закон регулирования может выражаться в виде нелинейной функции текущих координат, в которых задается параметрическая программа. Например, для рассмотренного в § 2.1 закона наведения как параметрической программы управления закон регулирования имеет вид (2.6), причем для его формирования берут исходную

информацию от измерителей расстояния р и скорости сближения р, т. е. тех величин, в которых выражена параметрическая программа.

§ 2.3]

СИСТЕМЫ С ПЕРЕМЕННОЙ СТРУКТУРОЙ

Нелинейные законы регулирования обладают богатыми возможностями во всех случаях, когда требуемый эффект может быть достигнут изменением свойств системы с изменением величин огаибок. Важньш классом нелинейных систем являются системы с неременной структурой. Больгаими возможностями обладают так называемые адаптивные, т. е. самонастраивающиеся и самоорганизующиеся, системы, описанию которых посвящаются нижеследующие параграфы.

§ 2.3. Системы с переменной структурой

Большие дополнительные возможности улучшения процессов регулирования дает нелинейное управление работой объекта путем изменения структуры регулятора в зависимости от размеров и знаков входных величин, поступающих в регулятор от измерительного устройства.

При этом могут использоваться комбинации линейных законов регулирования. Например, если известно, что при одном линейном законе регулирования получается быстрое начальное изменение регулируемой величины, но с большими последующими колебаниями (кривая 1, рис. 2.9), а при другом линейном законе регулирования - медленное изменение, но плавный подход к новому установившемуся режиму (кривая 2, рис. 2.9), то можно, включив сначала первый закон, переключить затем систему на второй закон в некоторой точке А, когда отклонение X достигнет определенного значения Xj. В результате процесс регулирования изобразится кривой 3 (рис. 2.9), объединяющей оба качества - быстроту и плавность процесса.

Для осуществления этого необходимо иметь в системе переключающее устройство, срабатывающее в данном случае при х = Xj (рис. 2.10).

Если в такой системе с переменной структурой все звенья линейные, то за счет указанного переключения, происходящего автоматически в процессе регулирования, система становится нелинейной. Это можно сравнить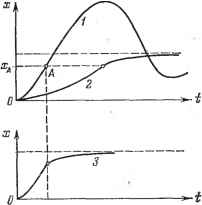

Рис. 2.9.

иптп Г. .-. усгпр

Регулируемый, объект

Рис. 2.10.

с тем, как получается нелинейная статическая характеристика из отрезков прямых линий (см., например, рис. 1.10, 5). Но здесь имеет место нелинейная динамическая характеристика, составляемая из последовательности разных линейных дифференциальных уравнений, соответствующих первому и второму законам регулирования.