2. Типовой входной сигнал следящей системы. В качестве типового сигнала для следящей системы часто принимают график изменения угловой скорости на входе в соответствии с рис. 11.22. Скорость сохраняет постоянное значение в течение некоторых интервалов времени (t\-> t%t tzt .)

Переход от одного значения к другому совершается мгновенно. Интервалы времени подчиняются закону распределения Пуассона (11.4).

В соответствии со сказанным выше будем считать, что математическое ожидание Q = О, а средний квадрат скорости равен дисперсии, т. е. = Во,фО. -График такого вида получается, например, в первом приближении при слежении радиолокатором за движущейся целью. Постоянное значение скорости соответствует движению цели по прямой. Перемена знака или величины скорости соответствует маневру цели.

Обозначим [Л среднее число перемен скорости за одну секунду. Тогда

J = - будет средним значением интервала времени, в течение которого угло-

вая скорость сохраняет постоянное значение. Применительно к радиолокатору это значение будет средним временем движения цели по прямой.

Для определения корреляционной функции необходимо найти среднее значение произведения

Рис. 11.22.

i?(T) = Q(OQ(iJ + T).

При нахождении этого произведения могут быть два случая. 1. Моменты времени if и f + т относятся к одному интервалу. Тогда среднее значение произведения угловых скоростей будет равно среднему квадрату угловой скорости или дисперсии:

2. Моменты времени i и i + т относятся к разным интервалам. Тогда среднее значение произведения скоростей будет равно нулю:

i?2(T) = Q(if)£2(if + T) = 0,

так как произведения с положительным и отрицательным знаками будут равновероятными.

Корреляционная функция будет равна

R (т) = PRi (т) + PR (т) = PRi (т),

где Р - вероятность нахождения моментов времени i и i -f т в одном интервале, а 2 = 1 - Р\ - вероятность нахождения их в разных интервалах.

Вероятность появления перемены скорости на малом промежутке времени Ат пропорциональна этому промежутку и равна у. Ат или -у-. Вероятность отсутствия перемены скорости для этого же промежутка будет 1 - .

Для интервала времени т вероятность отсутствия перемены скорости, т. е. вероятность нахождения моментов времени if и + т в одном интервале постоянной скорости, будет равна произведению вероятностей отсутствий перемены скорости на каждом элементарном промежутке Ат, так как эти события независимые.

И окончательно

i?(T) = Z)fie т Q2g т, (1180)

Знак модуля при т поставлен вследствие того, что выражение (11.80) должно соответствовать четной функции. Выражение для корреляционной функций совпадает с (11.79). Поэтому спектральная плотность рассматриваемого процесса должна совпадать с (11.78):

5оИ = т+ = . (11-81)

Заметим, что в отличие от (11.78) формула спектральной плотности (11.81) записана для угловой скорости процесса (рис. 11.22). Если перейти от углрвой скорости к углу, то получится нестационарный случайный процесс с дисперсией, стремящейся к бесконечности. Однако в большинстве случаев следящая система, на входе которой действует этот процесс, обладает астатизмом первого и более высоких порядков. Поэтому первый коэффициент ошибки Со у следящей системы равен нулю и ее ошибка будет определяться только входной скоростью и производными более высоких порядков, относительно которых процесс стационарен. Это дает возможность использовать спектральную плотность (11.81) при расчете динамиче- ской ошибки следящей системы.

3. Нерегулярная качка. Некоторые объекты, например кораб- -З-

ли, самолеты и другие, находясь под действием нерегулярных возмущений (нерегулярное волнение, атмосферные возмущения и т. п.), движутся по случайному закону. Так как сами объекты имеют определенную, им свойственную, частоту колебаний, то они обладают свойством подчеркивать те частоты возмущений, которые близки к их собственной частоте колебаний. Получающееся при этом случайное движение объекта называют нерегулярной качкой в отличие от регулярной качки, представляющей собой периодическое движение.

Типичный график нерегулярной качки изображен на рис. 11.23. Из рассмотрения этого графика видно, что, несмотря на случайный характер, это движение довольно близко к периодическому.

В практике корреляционную функцию нерегулярной качки часто аппроксимируют выражением

R (т) = Z)e-(HI cos рт, (11.82)

где Р - резонансная частота, [л - параметр затухания, D - дисперсия.

Значения!), [л и р находятся обычно путем обработки экспериментальных данных (натурных испытаний).

Корреляционной функции (11.82) соответствует спектральная плотность (см. табл. 11.3)

V - л Г 1 1 2й (1-1-Ьса2) д /1/1 оч\

В результате для конечного промежутка Ат получаем Устремив Ат ->- О и переходя к пределу, получим

Неудобством аппроксимации (11.82) является то, что этой формулой можно описать поведение какой-либо одной величины нерегулярной качки (угла, угловой скорости или углового ускорения). В этом случае величина JD будет соответствовать дисперсии угла, скорости или ускорения.

Если, например, записать формулу (11.82) для угла, то этому процессу будет соответствовать нерегулярная качка с дисперсией для угловых скоростей, стремящейся к бесконечности, т. е. это будет физически нереальный процесс.

Более удобная формула для аппроксимации угла качки

R(т) = Z?ee-4l (cosx + sin\x\) .

Соответствующая спектральная плотность

(11.84)

(11.85)

Здесь - дисперсия для угла, а = 2[л ([х + P) i, Ъ = -\- Р)-.

При такой аппроксимации дисперсия для угловой скорости получается конечной: Dq = ([х + Dq.

Однако и эта аппроксимация соответствует физически нереальному процессу, так как дисперсия углового ускорения получается стремящейся к бесконечности.

Для получения конечной дисперсии углового ускорения требуются еще более сложные формулы аппроксимации, которые здесь не приводятся.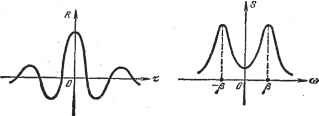

Рис. 11.24.

Типичные кривые для корреляционной функции и спектральной плотности нерегулярной качки приведены на рис. 11.24.

§ 11.6. Канонические разложения случайных функций

Элементарной случайной функцией называется функция, которая может быть представлена в виде

X (t) = х(р (t), (11.86)

где ф (t) -некоторая известная неслучайная функция времени (синусоида, экспонента, степенная функция и т. п.), х - случайная величина.

Если математическое ожидание величины х равно нулю, то и математическое ожидание случайной функции М [х (t)] = 0. Корреляционная функция в этом случае

R (t, ti) = М Ьф (t) x(f (ti)] = 1)ф (t) ф (ti), (11.87)

где дисперсия D = М [ж].

Рассмотрим случайную функцию х (t), которая может быть представлена

в виде суммы математического ожидания х (t) и элементарных случайных