Величина S (©) или S (2я/) носит название сшктралъной плотности. Важным свойством спектральной плотности является то, что интегрирование ее по всем частотам от -оо до +оо дает средний квадрат исходной функции времени х {t).

По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от со до © + d©.

В некоторых случаях спектральную плотность рассматривают только для положительных частот, удваивая ее при этом, что можно сделать, так как спектральная плотность является четной функцией частоты. Тогда, например, формула (11.62) должна быть записана в виде

оо -]-оо

j 5 (©)d© = A j 8Щ d© = F2, (11.64)

о -оо

где 5о (©) = 25 (©) - спектральная плотность для положительных частот. Однако в дальнейшем изложении будет рассматриваться спектральная плотность, соответствующая всему диапазону частот от -оо до +оо, так как при этом формулы получают более симметричный характер.

Весьма важным обстоятельством является то, что спектральная плотность и корреляционная функция случайных процессов представляют собой взаимные преобразования Фурье, т. е. они связаны интегральными зависимостями типа (11.54) и (11.55). Это свойство приводится без доказательств [108, 120].

Таким образом, могут быть записаны следующие формулы:

-НПО

5(©)= j Д(т)е-5 йт, (11.65)

- оо

+ 00

i? (т) = J S (©) eJ-t d©. (11.66)

- СЮ

Так как спектральная плотность и корреляционная функция представляют собой четные вещественные функции, то иногда формулы (11.65) и (11.66) представляют в более простом виде:

5 (ю) = 2 j Д (т) cos ©т йт, (11.67)

Д (т) = 1 J 5 (©) cos ©т d©. (11.68)

Это вытекает из того, что имеют место равенства:

gjBT - cos ©т + 7 sin ©т, g-icoT = cos ©т - 7 sin ©т,

и мнимые части могут быть отброшены после подстановки в (11.65) и (11.66), так как слева стоят вещественные функции.

Связь между спектральной плотностью S (ю) и видом функции времени X (f) заключается в том, что чем уже график спектральной плотности (рис. 11.16, й), т. е. чем меньшие частоты представлены в спектральной плотности, тем медленнее изменяется величина х во времени. Наоборот, чем шире график спектральной плотности (рис. 11.16, б), т. е. чем большие

частоты представлены в спектральной плотности, тем тоньше структура функции X {t) и тем быстрее происходят изменения х во времени.

Как видно из этого рассмотрения, связь между видом спектральной плотности и видом функции времени получается обратной по сравнению со связью между корреляционной функцией и самим процессом (рис. 11.14). Отсюда вытекает, что более широкому графику спектральной плотности должен соответствовать более узкий график корреляционной функции и наоборот.

Вычисление спектральной плотности неудобно делать по соотношению (11.61), так как это связано с трудностью предельного перехода. Обычно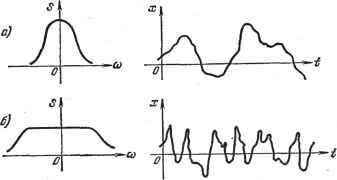

Рис. 11.16.

спектральная плотность вычисляется по известной корреляционной функции при помош;и формул (11.65) или (11.67). Эти формулы соответствуют так называемому двустороннему преобразованию Фурье четной функции времени R {%).

В табл. 11.3 даны некоторые функции R (т) и их изображения Фурье

5 (©) в соответствии с (11.65) и (11.67). В таблице используются импульсные функции б (т) и б (©). Эти функции, в отличие от импульсных функций, рассматривавшихся в главе 4, яв.чяются четными. Это означает, что функция

6 (т) расположена симметрично относительно начала координат и может быть

определена следующим образом: б-(т) = О при х ф<д и i б (т) йт =

о i,

= j 6 (т) = у ДЛЯ всех 8 > 0.

Аналогичное определение относится к функции б (©).

Иногда в рассмотрение вводят нормированную спектральную плотность, являющуюся изображением Фурье нормированной корреляционной функции (11.52):

.а)--, . (11.69)

+ 00

j 50 (со) Ло

где спектральная плотность 5° (со) соответствует процессу {х - х)\ и, следовательно,

- j S (со) dco = (ж - xf= D, (11.70)

- СЮ

где D - дисперсия.

Таблица 11.3

Двустороннее изображение Фурье четных функций

Ks п. п.

Оригинал

Изображение

9 10

б{т) 1

sin Q I т I cosflT sin(fi T+Tf)

e-lcosfiT e-( )cos fix

2зхб (ш)

Vn (2 ;.)

e 2fi

fi2 -ш2

зх[б(ш~й) + б(ш+й)]

cosTf> + n [6 (ш -fl)+6 (ш + fl)] sin я])

Q -co Q + co

a2 + (fi -co)a+ a2 + (fi + co)2 a , a

a L

Аналогично введенному понятию взаимной корреляционной функции (11.53) могут рассматриваться взаимные спектральные плотности Sy (ю) и Sys: (со), являющиеся изображениями Фурье Ry (т) и i? (т). Взаимные

спектральные плотности также являются мерой связи между двумя £тсА(со) случайными величинами. При отсутствии связи взаимные спектральные

: fj плотности равны нулю.

Рассмотрим некоторые примеры. 1. Для постоянной величины x{t) = AQ корреляционная функция равна R {%) =А1. Эта функция изображена на рис. 11.17, й жирной линией. Соответствующее ей изображение Фурье на основании табл. 11.3 будет

Рис. 11.17.

или, в другом виде.

S (со) = 2лА1Ь (сй) S (2я/) = Alb if).

Спектр процесса состоит из единственного пика типа импульсной функции, расположенной в начале координат (рис. 11.17, б).

Это означает, что вся мощность рассматриваемого процесса сосредоточена на нулевой частоте, что и следовало ожидать.

2. Для гармонической функции х = А- sin (coi + я])) была получена

корреляционная функция i? (т) = cos cOjT. Эта функция изображена на