Перейдя к относительным величинам, получаем в результате искомую вероятность

Р (11<х<12)= Ф(0.5)--Ф(0,25) 0.383-0,197 ОРЭЗ

Характеристические функции. Введем в рассмотрение функцию g (jX), связанную с плотностью вероятности w (х) взаимным преобразованием Фурье:

оо оо

M[e3] = g{iX)= J w{x)edx, w{x)= J g{j%)e-idK. (11.23)

Эта функция называется характеристической. Ее основные свойства следующие. Если случайная величина у = ах + &, то

(11.24)

Если случайная величина z = х -{- у, где х ж у - независимые величины, то

g. im = gx gy (А). (11.25)

Для нормального закона распределения (11.21) характеристическая функция будет

- оо

- оо

J exp[Axo~]dxp=exp[7?vx-J. (11.26)

По характеристической функции могут быть найдены моменты случайной величины. Разлагая g (/Я) и М [еЩ в первой формуле (11.23) в ряд Маклорена, имеем

g{m-2is()+pn,

M[e3>-]M[x] + M[Rn].

(11.27) (11.28)

Из сравнения (11.27) и (11.28) можно получить формулу для момента т-го порядка:

М [ж ] = 7- g > (0). (11.29)

АналогичньБМ образом можно получить формулу для центрального момента т-го порядка:

M[{x-xr]=n[-e-g{i%)

(11.30)

Формулы (11.29) и (11.30) могут быть использованы для вычисления моментов.

[(1-xi)(a;2 -2) ]= j j {Xi - xiy{x2 - X2yw{xi,X2)dXidx2. (11.32)

- CXI -00

Если g = s = 1, то центральный момент второго порядка имеет особое значение и носит название корреляционного момента: :

оо оо

ri2 = M[{xi - Xi) {Х2-Х2)]= \ {Xi-i){x2-x2)w(xi,X2)dxidx2. (11.33)

- 00 -00

В случае несависимости случайных величин xi и Xz можно легко показать, что корреляционный момент Г12 = 0.

РХногда употребляется понятие коэффициента корреляции, представляющего собой относительное значение корреляционного момента:

где Di и D2 - дисперсии величин Xi и Х2.

Для совокупности случайных величин Xi {i = I, . . ., n) в приближенных расчетах часто ограничиваются заданием матрицы-столбца (вектора) математических ожиданий х = \\ Xi xi и матрицы корреляционных моментов

f и 12 13 - Гщ

21 22 23

(11.35)

Гп2 1пз

Составляющие корреляционной матрицы показывают степень связи между отдельньши случайными величинами, причем г л = г. На диагонали корреляционной матрицы находятся собственные центральные моменты второго порядка, т. е. дисперсии Di = гц (i = 1, . . ., п). . .

§ 11.2. Случайные процессы

. Случайная величина х, изменяющаяся во времени t, называется случайным или стохастическим процессом. Случайный процесс не есть определенная кривая x(t), а является множеством возможных кривых х {{), так же как случайная величина не имеет определенного значения, а является сово-купностью (множеством) возможных значений.

Можно еще сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.

Векторные случайные величины. Пусть имеется совокуннссть случайных величин Xi {i = 1, 2, . . ., п). Такая совокупность может быть представлена в виде матрицы-столбца. Если физические размерности всех величин одинаковы, то матрица-столбец может быть отождествлена с вектором. При разных размерностях переход к вектору может быть сделан после нормирования (введения весовых коэффициентов).

Пусть, например, имеются две непрерывные случайные величины и Х2. Для них может быть введена двумерная плотность вероятности w {х, х). Если величины xi и Х2 независимы, то w {х, х) = (х) W2 (х).

Вводится понятие смешанного момента т-го порядка, где т = д -{- s,

00 00

М[хх1]= xxp;{xi, x)dxidx2 (11.31)

- 00 -сэо

и смешанного центрального момента

Примерами случайных процессов могут, например, являться: координаты самолета, замеряемые радиолокационной станцией; угол визирования движуп,ейся цели головкой самонаведения; помехи в системе телеуправления; нагрузка электрической сети и т. п.

Р1так, в случайном процессе нет определенной зависимости х (t). Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.

Однако случайный процесс может быть оценен некоторыми вероятностными характеристиками.

В каждый отдельный момент времени (t, t, tg . . .; рис. 11.11) наблюдаются случайные величины Xi = х {tj), Х2 = х (t), каждая из которых имеет

Рис. 11.11.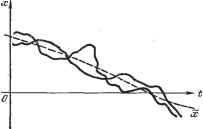

Рис. 11.12.

свой закон распределения. Поскольку это - непрерывная случайная величина, то надо пользоваться понятием плотности вероятности.

Обозначим W {х, t) закон распределения для всех этих отдельных случайных величин. В общем, случае он меняется с течением времени. Для каждого данного t в отдельности (г, t, tg, . . .) будет свой закон распределения:

W {Xi, ti), W (2, 2), W (Xg, tg), . . .,

причем no свойству (11.14) для каждого из них

\ w{x, t)dx = i.

Для каждого заданного момента времени можно найти характеристики случайных величин, определенные в § 11.1. В результате будем иметь среднее по множеству (математическое ожидание)

+ 00

X {t)= XW {х, t) dx

(11.36)

и дисперсию

+ 00

D{t)= J {x - x)w{x,t)dx=x{t) - [x{t)]K (11.37)

Среднее значение случайного процесса представляет собой некоторую среднюю кривую (рис. 11.12), около которой группируются все возможные отдельные реализации этого процесса, а дисперсия!) (t) или среднеквадратичное отклонение о (t) характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.