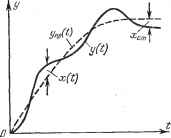Если принять линейный закон наведения, т. е. положить / (р) = кр, при котором уравнение (2.5) имеет вид

р + кр = 0, (2.7)

то окажется, что при этом Т = оо. Следовательно, линейный закон наведения не годится.

Обратимся к нелинейной функции вида / (р) = кр. Тогда нелинейный закон наведения (2.5) будет иметь вид

р + кр = 0. (2.8)

Оказывается, что при Ь > 1 величина Г = оо, а при b -< величина р = оо при р = 0. Если же

< Ь < 1, (2.9)

то Т конечно, причем р = const при b = Z, а в остальных случаях (Vj <

< Ь < 1) величина р уменьшается в процессе наведения с уменьшением р.

В результате приемлемым оказывается нелинейный закон наведения (2.8) при значении b в интервале (2.9). Конкретизация значения b внутри этого

интервала может производиться на основании каких-либо других требований применительно к каждой конкретной технической системе.

Итак, в системах автоматического регулирования и управления прежде всего задается тем или иным способом программа регулирования (в описанном выше широком понимании этого термина). Стабилизация неизменного значения регулируемой величины будет простейшим частным случаем программы регулирования Упр = const. Рис. 2.5. Программа регулирования i/np (t) будет

осуш;ествляться регулятором или системой управления неизбежно с некоторыми ошибками, как показано на рис. 2.5. Ошибка системы, (рассогласование)

X (t) = 1/пр (О -y(t)

обусловлена как погрешностями реальной аппаратуры, так и самим принципом построения регулятора.- При этом меняющаяся в. процессе регулирования так называемая динамическая ошибка х (t) может перейти в некоторое постоянное отклонение регулируемой величины в установившемся режиме при = const, называемое статической ошибкой хт-

Понятие динамическая ошибка является очень широким. В него включаются все виды ошибок систем автоматического регулирования, которые имеют место в динамических процессах, т. е. при меняющихся внешних воздействиях (возмущающих или управляющих) и во всех случаях переходных процессов. Различные виды этих ошибок и способы их уменьшения будут предметом изучения во всех дальнейших главах книги.

Величины динамических и статических ошибок регулирования в очень сильной степени зависят от структуры регулятора, определяющей так называемый закон регулирования. Этот вопрос станет ясным в дальнейшем, а здесь можно дать лишь некоторое общее понятие о законах регулирования.

§ 2.2]

ЛИНЕЙНЫЕ и НЕЛИНЕЙНЫЕ ЗАКОНЫ РЕГУЛИРОВАНИЯ

воздейстбие

§ 2.2. Линейные и нелинейные законы регулирования

Автоматический регулятор в системе регулирования состоит, как узке известно, из трех основных частей: измерительной, усилительно-преобразовательной и исполнительной. В усилительно-преобразовательной части имеются корректирующие устройства, в которых, помимо сигнала отклонения X регулируемой величины, образуется сигнал но первой производной dxldt (можетбыть также и но второй производной и но интегралу от отклонения j xdf), вводятся дополнительные обратные

связи и т. п. Все это служит для улучшения устойчивости, точности и качества процесса регулирования и будет подробно изучено в дальнейшем.

Закон, по которому формируется регулирующее воздействие и на объект (рис. 2.6) из нервич-dx

ных сигналов х, -ди т. п., называется законом

регулирования. Иначе говоря, закон регулирования есть алгоритм формирования целесообразного сигнала управления и на основании первичной информации ж, и т. п. В комбинированных

системах регулирования, кроме того, добавляется первичная информация но возмущению / (i), а иногда и но задающему воздействию g (i). Математически закон регулирования определяется уравнением автоматического регулятора. Различают линейные и нелинейные законы регулирования.

Кроме упоминавшихся выше корректирующих устройств, регулятор (система управления) может содержать различные фильтры (линейные или нелинейные) для борьбы с различного рода помехами. В усилительно-преобразовательном устройстве часто производятся также преобразования одних физических величин в другие (одного рода тока в другой, электрических величин в механические и т. п.) для удобства формирования закона регулирования в маломощных цепях регулятора, а также в интересах работы достаточно мощных исполнительных устройств.

Линейные законы регулирования определяются линейным уравнением регулятора, например, вида

Задающее Воадейстдие

Рис. 2.6.

2 да

(последняя скобка относится только к комбинированным системам). Для линейных законов регулирования детально разработаны многочисленные прикладные методы исследования (анализа и синтеза), различные расчетные и экспериментальные приемы определения устойчивости, точности и качества процесса регулирования, а также схемы конкретных технических устройств формирования линейных законов регулирования. Все это касается и линейных систем с неременными параметрами и импульсных и цифровых (хотя они пока еще менее полно изучены).

Что же касается нелинейных законов регулирования, то (за исключением релейного) они изучены мало. Очевидно, однако, что использование

нелинейных законов регулирования, определяемых разнообразными нелинейными уравнениями регулятора

){ W f s),

значительно расширяет возможности целесообразного изменения качества процессов регулирования и точности. Это ясно из общих принципиальных соображений, так как область нелинейных уравнений значительно богаче и разнообразнее, чем линейных.

Несмотря на то, что общей теории нелинейных законов регулирования нет, исследования и опыт применения отдельных частных видов этих законов говорят об их большой практической эффективности. Отсюда следует актуальность их теоретического изучения.

Введем следующую классификацию нелинейных законов регулирования:

1) функциональные нелинейные законы регулирования,

2) логические нелинейные законы регулирования,

3) оптимизирующие нелинейные законы регулирования,

4) параметрические нелинейные законы регулирования.

Важным отличием нелинейных законов от линейных является то, что они придают системе регулирования принципиально новые свойства. Если при линейном законе всегда вырабатывается сигнал, пропорциональный входной переменной или ее производной и т. д., то при нелинейном законе может существенно изменяться сам характер действия системы управления на объект в зависимости от величины входного воздействия. Другими словами, если для линейных систем изменение размера отклонения - это изменение только масштаба, но не формы процессов, то в нелинейной системе при этом может существенно изменяться и форма процессов, вплоть до принципиальных качественных изменений картины процессов. Эти особые свойства нелинейных законов можно выгодно использовать в технике автоматического управления и регулирования.

Рассмотрим отдельно каждый из указанных четырех классов нелинейных законов регулирования.

Функциональные нелинейные законы регулирования. Функциональными будем называть такие нелинейные законы регулирования, при которых регулирующее воздействие на объект выражается в виде нелинейной функции от отклонения регулируемой величины, представляющей собой входную информацию для системы регулирования.

Данный класс может содержать в себе как статические, так и динамические нелинейности. Примеры статических нелинейностей в законе регулирования:

: и==к{1 + Ь\х])х, u=k{signx) +

Б отличие от линейного закона, здесь в нервом случае будс! более энергичное действие регулятора при больших отклонениях х и больший запас устойчивости установившегося режима. Во втором случае будет менее энергичное, но более плавное действие регулятора вначале и повышенная точность в установившемся режиме, хотя и с меньшим запасом устойчивости. Однако такого рода рекомендации, как увидим в дальнейшем, справедливы для большинства систем, но все же не для всех. Поэтому они требуют специального обследования для каждого объекта регулирования.

Нелинейный закон регулирования за счет дополнительных нелинейных обратных связей может включать в себя также нелинейности от выходной величины и:

и = кх + F (и),