Взаимную индуктивность М определяют как отношение -si/ia или spiss/ii. Ни от 21, ни от is (и соответственно от ч *i) порознь она не зависит, если сердечники катушек неферромагнитны или сердечники выполнены из ферромагнитного мате*1ала с постоянной ji. Взаимная индуктивность М зависит только от взаимного расположении катушек, числа их витков, геометрических размеров катушек и от постоянной для данного сердечника р.

При любой форме и любом расположении магнитносвязанных катушек взаимную индуктивность М между ними без затруднений можно опрсделшъ опытным путем на переменном токе (см. § 3.38), Расчет же М при сложном распределении магнитного поля в силу трудностей математического характера производят обычно для катушек простейших геометрических форм.

Если мапппносвязанные катушки имек)тферромагн1ггныесердечники с непостояшюи ji, например обмотки намотаны на одном сер.дечнике, л которого является функцией результирукицей напряженности магнитного поля, то М -непостоянная величина.

Пример 21. На сердечник примера 18 кроме первой обмотки с числом витков ш,= 1000 намотана вторая с ШаБОО. Определить взаимную индуктивность между обмотками.

Решение. Если принять, что весь поток, созданный первой обмоткой. фШ!:1ЕА (см. пример 18) пронизываег и вторую обмотку (потоком рассеяния пренебрегаем), то аиФ и

д1 JWftln/R*

(2.22)

Подставляем числовые значения:

- .256.10-а 80 ЛООО. 500 2 - ЮЗ-0.41 ggg р

§ 2,4, Энергия магнитного поля уединенной катушки. Подключим к источнику э. д. с. Е индуктивную катушку с сопротивлением R н индуктивностью L. Пусть в момент времени /=0 в ней 1 = 0 я

По второму закону Кирхгофа,

£=и +и=Ш+*. (2.23)

Умножив обе части равенства (2.23) на idt, получим

EidiiRdt+id. (2.24)

Левая часть (2.24) представляет собАй энергию, отдаваемую источником э. д. с. за время dt, слагаемое £/?d/ -энергию, выделяющуюся в виде теплоты за время di в сопротивлении i?. слагаемое (йф -энергию, идущую на создание магнитного поля уединенной неподвижной недеформируювдейся катушки; обозначим ее dW:

dW = idt. (2.25J

Полная энергия, запасенная в магнитном поле катушки при изменении уз от О до

Для катушек с неферромагиитным сердетншим =1( н (f$=Z,d(.

Поэтому

(2.2g

где / - некоторое установившееся значение тока в цепи.

Пример 22. По уединенному с постоянной t цилиндрическому проводу радиусом R. ллиной I протекает ток / (рнс. 2.6). Вывести формулу для определении внутренней ннд>Ктивности провода, обуслов-тевной потокосцеплениад в теле самого провода.

Решение. В соотаетствнн с формулой (2.26) t= = 21Рн з. где под IP. поинмают магнитную энергию, запасенную в теле провода. В цилиндрическом пояске объемом dV=2nrldr (заштриховав на рис. 2.Щ запасе.

на энергия dW -dV. По закону полного тока. на.

пряжепиость поля Н равна току . пг\ охваченному окружностью радиусом г я деленному та длину окружности 2лг: И~ IrfibiR. Индукция B=JI.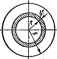

Рис. 2.6 Магинтная энергия

BHjTpCHHHH индукттвость провода § 2.S. Плотиостьэн!

имагиитиогополя. Положим, чтонакольце-вой сердечник, у которого отношение внутреннего радиуса к внешнему близко к единице (при этом можно с известным приближением считать, что напряженность в теле сердечника во всех точках одна и та же), равномерно намотано ш витков; /-длина средней линии сердечника. На основании закона полного тока Hl = iw или i=Hi/w. В свою очередь, d-wSdB и

Ф в в

Разделив обе части равенства на объем сердечника V, получим иотиостъ энергии магнитного ноля:

w,= WjV = {HdB.

(2.27)

Еслн H = COnsl, то В = имН и dBUMdH Cj\Cnnas>Ttyn,.

(2.2S)

Для ферромагишвого сердечника const. Поэтому гаш счстея,ерг единицы объема следует использовать фоу Т(2Щ.

S г.в. Магвнтная виертия магя1

даго онтура посСн пояер -

n ..ti;ir 1 >с д11.а7>!лы1счяъ уставшления. юков такая- .-h..,.

Подсшае агинту яиергию контуро. в первом вежи

по пр. .,=coml яергяя в.в.саетея ве только

пор , о , вер, овда эяертв.. з ис ,. в р ., ,р< . с,

взаимшндукции, -1Ч-Г м2. ииэтому энергия, обусловленная потоком

Расвд, алогяяяо, вр, устаноиея.и коа.во второму режвму о;,у,

(2.30)

Знак плюс перед слагаемым MiVa соогаеплвует согласному включению контуров, минус-встречному.

Запишем общее выражение для магнитной энергии системы магинтносвяэан-ных контуров. С этой целью ураененне (2.30J перепишем следующим образом;

Аналогичное выражение будет иметь к а п контуров-.

н магнитно связаны ие доя,

(2.30)

где %-полное потокосценление *-контура.

Пример 23. По обмотке ш, примера 21 течет ток 0,5А я ко обмотке lUg-ток 0,4 А. Определить магнитную энергию при согласном и встречном направлениях

Решение. По формуле (2.9), индуктивность в В соотвегствин с (2.30 пра С

орой обмотки £.3=0,

гри встречном направленна потоков

§ 2.7. Принцип взаимности взаимной индукции. Проделаем два опыта. В первом из них изменяющийся во времени ток <i;(/> пропустим по пЕрвой катушке (контуру) в измерим (подсчитаем) э. д. с. взаинкдацдукции, воиткающую во второй катушке (контуре), магнитно-связанной с первой:

Во втором опыте тот же ток (той же амплитуды и изменяющийся по тому же закону во времени, что н в первом опыте), назовем его пропустим по второй катушке и измерим (подсчитаем) э. д. с. взаимоиндукции, возникающую в первой катушке:

По условию опыта. ii(0 = a(0. поэтому ьягм. т. е. э. д. с взаимоиндукции в описанных опытах одинаковы. Это положение называют принципом взашшоапи взаимной индукшш.

Так.как Mi2 = Mai = M, то при определении т следует выбирать наиболее простой и удобный путь из двух возможных.

Пусть, налрнмер. через равномерпо нанесенную на сердечник обмотеу проводит произвольпо расположенный внутри сердечника провод (рис. 2.7). Этот провод является частью одновиткового контура, полностью ие показанного иа рисунке. Требуется найти вналлтнчеекое выражение для М иежду обмоткой сердечника и одновит-ловым контуром. Это ыожпо сделать двумя пу-

Первый путь: мысленно пропустим по первому понтуру (обмотке wt сердечника) ток (i, найдем пстготоаюпленне второго (одновиткового) пон-тура с потоком первогонопределимЛ1=111/1,. Второй путь: мысленно пропустим по второму

>f , U. (одиовитковому) контуру (обмотке е)2=1) ток i,

. L J-X найдем потокосцепление первого контура f с по-

I током второго и определим М

В расчетном отношении эти пути не эквивалентны. Первый путь много проще второго. Объясняется это тем, что поток, создаваемый первым контуром, весь замыкается внутри сердечника в полиостью сцепляется с одновитковыи контуром. Следовательно, потокосцепление If 1, можно легко найти. Определить же поток, создававмь[й- одновитковым контуром н сцепляющийся со вторым контуром, i сердечника произвольпо, затруднительно. Поток сетдечника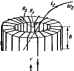

Рис. 2.7

[ провод расположен внутри

Потокосцепление fe-hpi< ,=1 .Ф5=ф.

Взаимная индуктивность между обмоткой ич v одновитковым контуром

(2.31J

Пример 24. Через сердечник примера 18 пропущен одиночный провод. Найти М между одиночным проводом и обмоткой w Решение. Hq формуле (2.31) [ср. с f2.22)], при ш=\ ,.,25в-Ю.80..000.2->0-..0,41 3, мГ.

Пример 25 По одиночному проводу примера 24 проходит ток =100(1-е Определить э. д. е., наводямую в обмотке оу. Решение,

емх = - М1 = - 0,131 10-3- О0-2ё = -О,0262е- В,

§ 2.8. Коэффициент связи. Под коэффнпиентом связи k двух магнитносвязанных контуров с нндуктивностями Lia и взаимной индуктивностью М понимают отношение М* к VLJL:

(2.32)

я L и** водьше (или L, но не ожег быть больь

Докажем, что k не может быть больше единицы. Дли этого составим выражение для кК и если выяснится, что *=/=1. то и k\. Воспатьзовавшись обозначениями § 2.3, запишем

.1(Ф1.+Ф )

+5W- (< 1.+Ф1)(Ф.1+<о )

гя-

Рнс. 2.8

Коэффициент связи k= 1 только в случае, если весь поток, создавае-ьшй первым контуром, сцепляется со вторым,

§ 2,9, Закон электромагйвтной инерции. Правило Ленца. В 1883 г, русский академик Э. X. Ленц установил закон электромагнитной инерции, получивший название закона или правила Ленца.

Формулируется ои следующим образом: при всяком изменении магнитного потока, I ] *

щепляюигося с каким-либо проеодяищм I 1°

контуром в последнем возникают силы

электрического и шушшяеско шроктера, апремящиеся сохранить постоянство магнитного потека.

Сила электрического характера означает, что при всяком изменении магнитного потока, сцепленного с замкнутым проводящим контуром, в этом контуре возникает индуктированная э. д. с, которая стр€*штся вызвать в контуре ток, препятствующий изменению потокосцепления контура.

Механическая сила, воздействующая на контур, препятствуег измвтению линейных размеров контура или повороту контура.

Пример 26. Перпендикулярно равномерному и неизменному во времени магнитному полю (рис. 2.8) 1Шдукции В = 1,5 Т расположен прямой провод длиной / = 0,5 м. Гибкими проводниками он соединен с нагрузкой R . Полное сопротивление замкнутого контура/? = 20 Ом. Рассмотреть что будет происход1ггь при движении провода.

Решение, Если провод негюдвижен, то в нем не изведется э. д. с. и на него не действует механическая сила.

Если же провод начнет двигаться, например, влево со скоростью 10 м/с, так что контур будет оставаться замкнутым, то в нем наведется э. д. с. [см. (2.5)]

e=Bfo = 1,5.0.5-10 = 7,5 В (а)

и по проводу пойдет ток

1-=с;/г = 0.37б А. (б)

При движении провода влево поток в контуре от внешнепт маг-питного поля иозрастает. Ицдуктиронанный ток (направлен по часовой стрелке) вызывает магнитное поле, направленное встречно внешнему полю, и прспятспщет росту потока контура. .