Между отдельными элементами механической с вующен еВ влектрвческой модели (системы) может *ыть анался двух 1 в соответствии с тем, что для наждой ялектрнческоЙ цепн может (йлъ с дуальная ей цепь.

В первой тапе аналогий сопостввимымн величинами являются: сила напряжение ы. скорость w-ток t, масса т-нндуктнвиость L, иодатлявость-Ш пружины с-снкосгь С. сопротивление трения /р-электрическое сопротивлЯ иие R. 1,-1

Во втором тапе аналогий сопоставимыми величинами являются: сила /-гш/Ш скорость о-напряжение ы, масса т-емкость С. податливость с-индуктивноед, L, сопротивление трения гр-электрическая проводимость С.

На рис. В.1, в изображена электрическая схема по второму типу анал соответствующая схеме замещения механической састет)ы рис. B.I, а. Дпя л

*С+1+*0= . или C + udt-\-Gu=Hl).

где U-напряжение между узлами а я Ь.

я напрмгения и во временя в схеме жс. B.I. всоотве кенеиия скорости о в системе рис. B.I, а, еслн параметры злектр) гветствующвм образом подобраны.

ПРИЛОЖЕНИЕ Г

СЛУЧАЙНЫЕ ПРОЦЕССЫ В

ЦЕПЯХ

§ Г.1. Случайные процессы. Ко jbcceohbko систем, находящихся в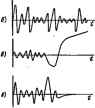

еляционнме функции. Положим, что есть [ннаковых условиях, и в вих происходя? в принципе одинаковые процессы. В силу влияния на процесс различных случайных факторов, имеющих вероятностный характер, процессы в систшах но--ут несколько отличаться друг от друга. В результате наблюдения можно устапо-вить, какая величина при фиксированном моменте времени / является наибол№ вероятной. Плотности

процесса обозначают ()

ражает собой вероятность того, момент- вреиевн t значение вели находится в интервале от х до x+dx. Функцией распределения F{x) называют вероятность наступления события, при котором Значение величины л;, характе ризующей это событие, находится тервале от -со до х.

Случайные процессы могут ferrb разделены на стационарные и нестационарные. Стационарными называют случайные процессы, для которых все функции распределения не зависят от изменения начала отсчета времени. Для нестацио

парных случайных процессов фу1------

Рв(. r.I рвспределелия эавпсят от времеин-

В качестве орвмера на рнс. Г.), а, б иэображе[ы кривые иекопфся-о стацво-нариото случайного процесса. Дня этих кривых вероятность возиикнове ния колебаиав с некоторой аиплитудоВ остается той же, еслн сданиуть начаш

отсчета вршеии. Иная картвиа имеет место на рис. Г.1. в, *. t

кривые x (О для некоторого нестационарного случайното проце а.- На рис Г I в начиная с ии(оторетч) момента времени ж неотраииченво возрастает, а на ркс. Г.1, е-стремится к нулю. Ясно, что для этих кривых сдвиг начала отсчета времени измеияет вюятмостные зависимое .

Для стационарных случайных npdoeccob среднее го множеству (обознэ- ется к) равно среднему по временя (обозначается <х . т. е- х=(х>.

Это положение называют .tpevduveaiou теоремой Гипотезой). Эрпфическаи теорема служит основанием для того, чтобы, обрабатывая всего одату на временных зависимостей х ((). полученную экспериментально, судить о статистических свойствах веек заенсимосгей х(/) прн стационарном случайном процессе в изучаеюй снеге- xfi,

Для ;

шх случай-

ных процессов х(() вводил ную и взаимную корреляционную функц Авпижорреляционная функция е ся мерой взаимной связи фикции нфут-цних((+, смещенной по отношению к х (() иа время х:

xit+x)di. (Г.1)

Свойства Л(т):

1) (т)-функция четная, т. е. Я(-= --R (т) [в этс*) Ложно убедиться, введя в (Г.1) новую переменную lt=t+-i\;

2) если ж(0-функция шриодическая, то для нее R (т) может быть пр-дст;1влена в виде суммы автокорреляционных функ ПИЙ с ной и от синусоидально изменяющих лнющих;

xU) имеются гармоннческпе составляняцие, то R (т) не содержит информации о начальных фазах гармонических состав- Рис. лающих;

4) для xU) без постоянной и гарЪоннческнх составлямицих Ri при %0:

5) для случайных функций времени без постоянной и гармов ляющих R(r) уменьшается с увеличением т н уже прн сравнител! стремится к нулю [объясняется это тем, что для чисто случэнног чение x(f+T) уже при относительно небольшом т не зависит от которое имела эта функция х(() в момент времени f].

Взаимной корреаяционнаа пункцией Rj,y (т) двух функций t называют функцию, определяемую следующим образсм:

2f \

Функция Rxy{4) является мерой взаимной связи двух случаКаых функций времени.

На рис. Г.2. а изображены две произвольные функции времени: хЩяу(Q, которые позволяют и№Лядко пояснить свойства функция B,j,(t).

1. Функция J? (t) аавнсвт от того, сдвинута функции в(0 iia --т или иа -t, т. е. R:tA--*Rxj,{-).

Еслн всю кривую УЩ рис. Г-Й, а (даинуть на +т влево, т. е. взять функ-№по s(+t), то 1фовэв№иие x(Oif(t+t) удег равно нуло для любого*, а адачит, rj,(t)=0. Еслн же вш кривую у if) рис, Г.2, а даавуть в& -т

вправо, т. е. взять функцию tf -г), то на нмсотором интервале времени г веденве ордават кривых х(() и yil-t ие Судет равво нулю.

2. Савиг функции yil) влево на т дает тог же результат, что функции дг(0 вправо на -т. Поэтому ЛхАг(т)=Л(,л(~г).

3. Для случайных функций времени х(() в у{1). ие содержащих постояннЛ в гармонических составляющих одинаковой частоты (для некоррелированных

функций). R.j,(x)=0.

I Фурье для слу

§ Г.г. Прямое и обратное преаб[ nieiWHH. К случайным функциям гоемеив и к нх корреляционным 4 применяют преобразование Фурье. Так как в общем случае случайная времени *(() илн ее корреляционная функция может и ие стремиться к нуЛ ! 1фн /- -±со, то, для того чтобы к ним можно былорнменить преобразовам Фурье, поступают следующим образом: преобразование Фурье применяют к фую ВИН JCitf). котсфая ие равна нулю в интервале от -Т до +Т в равна нулш)! вне этого интервала. Если затем Г- -со. то JCj (() будет стремиться i я Фурь& зображекие функции Xi(0 будет стремиться к Фурье-изобр! функции к (()

Подобное рассуждение может быть проведено и по отиощеняю к Фурье-1

а ftjt (X) называют

5,(и)= S it,(T)e-idT.

Rj, (т) e-A =it,{T) (costoT-/ йп ол). Еслн учесть четность it, (т) и cos я и пметность sinan:. т

Sj, (о))=2 j (т) созт dx.

(Г.3)1

где Я;,(ш)-сне11тральн4

Ггг следующими свойствами: ч денс! четная; 3) так же как и Rj,{i). если таковые содержатся в jc ((). Зная Sj,(fa), можо определить ;

случайного процесса, которая ггельна в положительна при всех частотах; 4 содержит информации о фазе га))МОНик. I

S,(cu)e° dT.

К(ю), воздействует спектральная -------

с передаточной функт г функция спектральж

ь котороВ ]

5жв И= ( )5, ( )-

н его свойства. Представим себе прямоугольный l

в гредеяе бесконечно малой длительности (рис. Г.2, б). Нет

убедиться в том, чго для него Rj,ix)0 только прит<±~. Виеэп

тервала Rj,(x)=0. Иэ предалдущего ясно, что если it,fq=0 то- - малых т, то процесс, которому соответствует эта qratOHH, иЯнын.

Положим Tenq>b. что it,(T)=e~ fPKHb быстро спадает в фуикцнн х п

где а очень велико, поэтому I закону экспоненты (рнс, Г-2,л). Г*

И для ВТОГО случая. По опрвделеник

*( )= f ,(т) e- *dT=2Re J R,{T)e- dT=

= 2НеГе-е-<.т.2 е[] = .

построен график 5,[и). полагая,

Если а очень велико. :

ется только при очень больших ю, соизмеримых с сть Sjc (ю) кратковременного игольчатого импульса

На основании изжокеиного можно сказать, что чем уже импульс (чем он короче во времени), тем шире его частотный спектр.

Белый шум представляет собой совокупность множесгеа беспорядочно и без всякой етязи следующих друг за другом игольчатых импульсов (рис. Г.2, Sj, амплитуды которых имеют случайный характер и подчиняются нормальному закону рнспределення вероятности, при котором плотность распределения вероят-иости

1 --

паэоне частот, т

icKoe ожидание; коэффициент о-дисперсия, рность кааадого импульса постоянна в достаточно и для белого шума Sj((ta)=const.

§ Г.4. Источники внутренних шумов в мекщическнх цепях. Активные сопро-тивлення. электронные лампы, транзисторы, магнитные усилители и многие дот-гие элементы схем являются источниками внутренних шумов. Э.д.с.. которыми можно в расчетном смысле мшивалентировагь эти шумы, обычно очень налы и составляют часто несколько микровольт. Если шумящие элементы схем включены на вход усилителя, имеющего очень большой коэффициент усиления, то шумы ограничивают порог чувстентепьнбстя схемы и с ними приходится счи-татьо

Активное сопротивление как иагинник шцма. Вследствне хаотического теплового движения электронов в гейвторый момент времени в

je усилители и многие лру

lli вознйкаюн

i сопротввлеьни J? фм), является белым шу-о плотность

5 (е))=2АГД. иана, равная 1,38.10- Дж/граж Т-абсолютна? тем-

Шумящее сопротавиение в расчетном смысле эквнвалеятно схеме рис. Г. а, В ней последсяательво соединены вешуиящее ссоратвлюпе в источник э.д. с

ШВ А-постоянвая Во)

t/Si = 5щ (ю) Д щ/я=Ш-R tf.

Через Д О -чкно В1уийдее с

Дюбаюй ЙМИШ < вдтияоа Эффект вспускашя .яектрожя и

икмГ1 1и iocm случавныЕ карактер. В векогорыВ оииг времен, иэ инп накала вылетает больше злекровов, в смежны с в м 41 -!* .

В результете анодный ток ири отсутствии сигнала иа сетке лампы непостоянен и имеет некоторую переменную составляющую, которая колеблется около среднего

IKT S.°a дро ..ы . так как о, иавомяи. п . юбниок при к у ?Гмип,о.ь. Шум. выаваиныВ дробовым таокс нетс. бел у- .

Ьо Гспектрвльи.я шоность которого не заявскг от частоты. В расчегно смысле .j дробовой эф4ект учитывают, включва в сеточную день лампы tpHC. I Л. О) яеко-

%TMTo K*,;.SjoB\=y :&SZ=

крутизна характеристакж лампы, мАуВ. Для ыногосеточных ламп значительно вольте, чем для триодов.

ПРИЛОЖЕНИЕ Д

РАСЧЕТ ЭЛЕКТРОННЫХ И ТРАНЗИСТОРНЫ СХЕМ

14ЕТОДЪМ IIEOnPeAEIEMKM мдтриць

И ДВОЙНОГО АЛГЕБРАИФСКОГО ДОПОЛНЕЮШ

Метод основан на г

ределеиных матр:

ыевтов схем, составлении не<шределея1 яучени!

L проводвмостеи ле-стей всей схемы, по-столбца и строки, соот-

и строки, со lee формул д

е метода начнем с вывода формул У-аа-

раметров трашвсторт?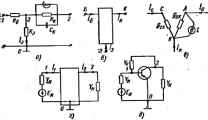

I Д.1. Чирамеч1Ы гшввстч . Составим уравиенив во методу уалтык т-тенцяалов для узла 5 схемы с с шаы эмиттером рмс. Д. , а {см. рис. 15.И. б), полагая Гс-ЧКЛ

Точки 1, S, 3 имеют потенциалы ф[, фв, фч. а точка О имеег i rjeo-n+V.+nC- *

.-(Ф1-ф4)* -Ф11. + >-.(1-0)1-ф,-

В свою очередь,

.-(Ф,- 1.- ,-Ф.-

Сопоставляя два последних уравнения с в Кюрме и заменяя индекс 1 нз б. индекс 2 на к, получим

чешрехполюснива

СД-1)

Порядок величин для низкочастотных ыаломсшвыл трвнзвсгоров следующий: Убб 10- Ом-, Кик=34.10-е Ом-; Уб=--10-0 Ом-1. К.б 32-10- Ог1.

5 Д.2. НеопредЕлсянвя метрица уэловых npoboj ставим трананстор трехполюсннком (рИс. Д.1.б)с /в, /s направим сюответственно к зажимам Б, К, Э, ф отсчитываемые от нулевого уровня О.

Составим выражения для токов и /,

Т тгкХ

потенциалы фй, ф а тока получим,

/б= У 66 (Фб -<р )+1вж (Фк-Ф,>; /,-(1бб-1-> в) Фв+(1 б-f Ie.-f Ф.-(>в.+>.Фк.

Эта система урзвяенай в матричном виде запищется так:

1п=1У]т

\Y]=

у €6 ~(Убй+Уб)

я матрица узловых пршодимостей.

В иеопределмпюй матрице сумма элементов любого столбца и ЛкЛзй строки равна нулю. Иэ нее получают утороченную матрицу, вычеркивая тот столбец и ту строку, которые соответствуют аазленвсжу узлу гхемы.

Л алектронной лампы. На

§ Д.З. Неопределенная иатрина узловых npoi

:. Д.1.вв -

ряс. Д,1, в изображена схема, йоогветствугощан схеме рнс. 15.30, в. В ней имеются три узла (С, А, К), две прсиоцимосга: g =g и йс-внепшяя проводимость ыежду сеткой и катооям (в частшш случае она может отсутствовать).