в Б,2. 06iqas харитфиспша применение иа-фяц

применяют для: в) сокращенной запчся систем уравнений; 6) у

---------------- Л: в).

уравнений-, .

свойств здектричее!а1А цеяеВ tpt.i например, (З]), в теория графов, прв сийтезе цепей, при нспольэованнн ЭВМ и т.

Упорядочение решения систем при помощи матриц проиллюстрируем f

мере составного четырехполюсника. ftl

Пример 177. Составнп. цатряцы Ш В MdV

двух каскадно соединенных четыреяпояюснвк-J и 2 (рнс. Б.1) в атрнцу 9квивалентного i четырехполюсника.

Ряс, Б.1 , Решение. Для первого четареяшлюсиикя

Для второго

Заменив j* в правой части (а) ва его эквнвалеш нз (б), получим iWaipmw двух каскадно соединенных мтрехпояюсннхсв

ftlX чииг--------

Таким овраэои.

игра*,..

а 4 узла i

§ Б.З. Основы ма1ркчпой теши ной схеме. Так, в схеме рис. B.2.,

них стрелками полсвугельные нап.

одно ва возможных деревьев в схеме (рнс Б.2, 6). Ветвв взобраэвм аышшиаЗ

1ы-пунктирными линиями. Фрндамаапалшлми контурами называют контуры, в каждый на которых 1 входит только по одной хорде. Так, для дерева рнс. Б.2. б mieai три контур Г о, Ь, с на рис. Б.2.в.

Мапицей фундамеюпалымх контуров (/TJ называют таблицу из чисел Ц --1,0, в которой строки (итщекс О Ответствуют контурам, а столбцы (индекс/)-

- I. если ветвь ве i,v., .v - . typH по часовой стрелке, вапишеи

вс1Т тятся-О, Для I

ера, об одя, I

Контуры

Ветви 2 3 4

йр О О 1 1 0 [ 1=6 О -110 I о! ell -190 О -lj*

Матрицу m используют для записи ypai Для того чтобы ог заданной схемы првЬя

Еслн прв обходе 1-го контура стрелка па в

; обхо!

дом контура, то в соогвегсто1№й клетке таблицы спвэт I, есля встречI , х 496

------ н заданной схемы пп 1гя * °° РУ ЭЭКОну КярХГО.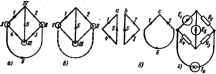

тсеасния. а вомер croW V- мест 2тво То соотетуе, иомару тем (кружком) и рмк?4 TSLSib!tf - аетствующей клетке таблицы ставит I епл. P-t* еоот.

. ровута тсевием -0. ЛиТГаийо SS?a -

Отсечения

Ветви

1 О О

о -1 ! .00 I

О -1

о I -I о

с помощью С]-нз1рнш>1 уд Кирхгофа. Ее используют также для шалов и по методу контурных токов.

у2?Сииа?ош 1 - 1> далвио. с,ем и K]-.Tp,B?SST S np £ Р ной тори, гри исволиу , . [И

к. Si.iZxtSZST- е. К]- .триду.

. удое

ваписывать уравяения ио первому акону эалисн VDanHe B во егоду уадоаык поген-

юдля в 17

X возможных ковтуроа схемы.

как и (Орматривд. f.....

Запись уразненнн се

;з2шп?яУйнов не ветвих через в галексмой или оперэтормой формах, т. е.

0)ставвм уравнмжя по первому закону Knpxi сечениями I, II, III на рис. Б.2. а, используя [(Д.

)хгофа для узда , i

Отсечения I 1 Г-1 II

0-1-1 О О О О 1-1-1

При решении зиик!! -. ...h.vuud-..1 к-

,ра.нешя для < ftZJtSumy<! > уривения J = f.e r =,-L p.EL,a U> . яи.

bTpSS cCic o pen, , и- <> rSn;

R, Sis V-

вдоль трех фундаментальных контуров рис. В.2. е.

: задач

, основные обычно приню [ контуров-

Перестави,

Перестагам строки в столбцы в (г) так. чтобы ие требующиеся по условию вадачи гокв /, /3, / можно было выразить червз It, U, /*:

-I -I о о о 1>, О

Заменим матрицу

е эквнвалеят из (

заиенвн иа правую часть (д):

; строки и столбцы так, чтобы можно было Бьщелнть подмвхрв*

1 6 6 2 О 1 01-I

1-10 0 0 -1 0 110

I 01

0 0-

\-0; И

о -11-1 г 1 I

.0 -1

-1 о 1

- 1 о о

1 1 <пг л о о 1 1;<о.

L 1 о oAlvA

Послеповетельво умножии четыре матрицы. Окончательно

0 1 0-ги,- - <к,+ад -m,+ri -

1 1 о с, -R, о 1 о l Ll/,J L я. R.

-R. /,

и.

Черев матрицу отсечений [Qh диагональную матрицу прсводимостй! схенц Ig] я транспоиировйниую мат1дацу отсечений [Qj можно определить уаловую матрицу проводимостей [CF. используемую для записи урапиеивй уаловьа

Например для схемы рис. В.2, а, полагай, чТо проводимое ветвей l-=jB равны gi-gf (а ветви 6 источник мкв н потому ее проводимость 0) и что узел Jjt. ваэемлеа, имеем

- 1 о о -1

о о

Еслн учесть, что матрицу узловых можно записать в вцл ыатца-строка токов

fii + S -fii

в в методе узловых поГенциялов [Гр

в Biwe-C]/fc]-HQ]l£l£f. где (/tl -транспонирование Я ветвей с иегочникамн токов I/ шунтярукшнни ветви я, о уравненкя по ммеду

где [ф1

а-столбец узловых

методу контурных -Лжов можно записать

Аналогично, матричное уравневпе е ввде

1г1 [Kf [/J-lKl 1£ Г-1К1 И [/*.

Здесь матрица фундаментальных контуров; М-двагоиальная матрица

сопротивлений ветвей {матрица полюсных уравнений); /сГ-транст /С} атрвца, транспонированная мтрнца-строки s. д. с. источников

а. д. с. ветвей. Со знаком плюс топ источника тока входят в если по

шунтнруюшеЙ его ветвн к ов дает топ, согласный

ПРИЛОЖЕНИЕ В

исследовамс лр0цесс09 в неэлвс1ри с1сия системах на электрических моделях-аналогах

Иссл(

ческнх. тепловых гцдр

и др.)

, акусп

мер, в *лвпрс еханичес8кх) часто производят Стремление использовать для этой цели тем, что: 1) электрические параметры можн. - . .

делах; 2) тока и напряжения ыожпо измерять с большой точностью; 3) напряжения относительно просто записать на осциллографе. В качестве неэлсжтрв-ческих будем расснвтрваать механические системы.

о иеэлектри ческнх (напрн-исктрических моделях-аналогах, нгрические модели обьясняетсв > легко изменить в широких пре-

поступательного, вращатель-

1к=Гв г. -

Активными являются нсточннни силы / и источники скорости с для систем Поступательного движения и источники вращающего м<шента М и угловой скорости ю Д№ систем вращательного движения.

Пассивными являются элементы упругости, трения и массы Как и прн пас-сйотревни электрических цепей, эти элементы часто идеализируют, вацрито -етот, что Цдеальная пружина обладает только упругостью и пе имеет inccu. Лля заданиоП механической системы сначала составляют схему замещение 1ежду механическими и алектрическнмн величинам далее), образуют электрическую схему-аналог, которую {эксперименталыюму или теор*ическ(Я1у). мы замещении мсханвческоб системы необходимо: :чста для сил и скоростей (илн соответственно для угловых скоростей);

а затем, испольяуя

{о которой Cyj

в подвергают i

Перед составлением 1) выбрать систйлу

вращакйцих моментов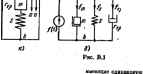

2) соединять между собой узлы, вую величину смещения;

3) соединить иеиоданжные узлы в один yseJK

4) на схеме замещения между соответствующими узла*

е элементы, имеющиеся в научаемой ( Рассмотрим простейший пример.

еханнчесмя система рис. В.1. а образована телом массой п

b пружину упругости S(S= где е-податливость). На тело действует в

я сила /(0. являющаяся функцией ври-вни i. Прн движении тела в вертикальном направлении возникает вязкое трение о среду. Сила вязкогц трения ГЛТг~ 3 Ч в с. е . . д.. УЗ :

Выберем положительное i тела x, I

тельное направление для скорости

изображена иа рис. В.1. б. В ией четыре

о второй масса т, в третьей-идеальная пружи!

ie для отсчета величины перемещении тела при отсугствив силы /(/)- Потожи-показаео на рнс. В.1, а. Схема замещеняя В первой Е

а упругости S, в

е прения гр.

схемы замещеная составим уравненпе но первому закону мехаиики. Соглисно этому вакояу. сумма всех впяпнвх сяЛ, действующих в некотором узле, должна быть равна сумме сил реакнвй е этом же уэле. В узле а действукгт три силы реакции: / =т -реакция системы, обусловленная силой внерцин;

/*=-J Л-реакция системы, обусловленная деформацией пружины; = = Гтрй-реакция системы, обусловленная трением. По первому закону мехапикн.

U+h+lv-IO -+J-J<.d(+/,-,(0.