в соответствий с рис. А.15, й--ж

Д<у=сЧ-е: А/=1.

Таким образом,

A=(o+d-J-fi(a+c6+te)+<KJ(fr+0+flf(b+e>+d/(c+e)+ . (а) теперь найдем Д для схемы рис. А. 15, а разложением по путям между .узлами 1 и4 (зачерненные кружки на рис. А.16, о). На рис. А.16. б-е пока-!заны пять возможных путей между узлами i и 4 и соответствующие им подсхемы (подграфы) для нахождении Д.

Рис. А.15

<i> -о

Для первого пути по □ пуги; Pi=ee.

собой параллельное соединение ветв /, с, Ь. Следовательно, A(=/-J-c-J--

и е Pi равно пршэведеяию протодимостй - * о а с подграф представлиег

е) V< г}

Рис. А.16

д) е)

Для второго пута (рис. А.16, по ветвям /, 6 Pa=fb: Дд=в4-е4-с. Для третьего пути по ветаи d (рис. А.16. г)

P=d; Да=(о+е)с+(о-Ье)(-1-6)+с(/-Ь6). Для четвертого пути по ветвям а, с, Ь (рис. А.16, 5) р4=сА, Да=1, Е при закорачивании ветвей о, с, b граф вырождается в точку.

Для пятого пути е Таким образом.

м /, с, е (рно-. А.16. с)

+d[(a+e>c-b(a+e)(f+b)+(f+fc)c)+ec6+/ . Результаты подсчета Д обоими нетсщами совпадают.

что проводимость i

.. выбранной ветви. Положим, 1ыбранной вегеи графа равна а. Тогда определн-

т по формуле

Д=аДа-}-Д .

(А.24)

ь графа прн коротком замыкании ветви а; Д -определитель

в § А.7, формулу нмостен, передачи

где Дд-определит графа при раэомк!

§ A.I2. Применение основной формулы. Как (А.2) применяют для определения входной и по току, по напряжению и в других целях.

Рассмотрим вопрос о том, как ею следует пользоваться. Обозначим тип узлы графа, к которым присоединяется ветвь, содержащая нсгочияк питания схемы. В дальнейшем полагаем, что источником питания является либо источник э. д. с, либо источник тока, поскольку к ним можно свести любой реальный источник питания. Кроме того, считаем, что источник питания только одни. Еслн же источникоп питания несколько, то следует воспользоваться прнншшом наложения, последовательпо находя искомую величину от действия каждого из источников, учитывая при подсчетах внутренние ссифотивлении последних.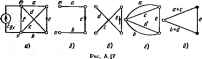

Под В в (А.21) подразумевается либо напряже .

Б ничесгае посяеиегЬ взят источник э. д. с, либо ток / источника тока.

В качесгае тока / в числителе левой частя (А.21) берут ток по той ветви, по отношенню к которой нужно найти искомую величину. Еслн необходимо определить передачу от источника питания к некоторой s-fi ветви, то под / понимают ток в s-й ветви.

Число слагаиаох в числителе (А.21) равно числу возможных путей между узлами тип, причем каждый из них должен проходить по выбранной s ветви (путь через источник питании ие учитывают).

В сумму C,Lr часть слагаемых может иходить со знаком плюс, часть со званом минус, так как С, может иметь знак либо плюс, либо минус.

Для того чтобы определить, никой зник будет иметь С руконодствуюгся следующим: произвольно выбирают положительное направление вдоль ветви s (ставят стрелку из ветви s). Если при движении по пути С, пройдем по ветви s согласно с положительным направлением этой ветви (по стрелке на ветви), то С, берется со знаком плюс, в противном случае-со знаком минус.

Вычисляя определитель системы Д. следует учитывать внутреннее сопротнв-ленпе источника нитания схемы. При питании схемы от источника э. д. с. Д под-счшивагот прн закороченных узлах тп (внутреннее юпротнвление источника э. д. с. равно нулк*. При питании схемы от идеального источника тока ветвь тп, в которую включен источник, прн подсчете Д разрывают.

Пример 173. Определить взаимную проводимость ветви с источииком э. д. с, (подключенной и узлам тп) и ветви с проводимостью е (рис. А.17, а).

Решение. Для учета знака С, примем эа положительное накравление ветви е, указанное стрелкой. Тогда

*/£вх=2:с,дд.

в графе есть две пути между узлами . . ,......

Первый путь йаображен на ()ис. А.17, б: Ci=aeb. Этот путь берется со

плюс, твк как при прохождении, его по------ -------.....--------------

ннем стрелки нв этой вет&н. Поскольку прн ззкор того пути) граф вырождается в точку, то ui=l.

Второй путь Са проходит по ветвям d, е, с {рнс. А.17, с). Так как пр хождении этого пути по ветви с проходим встречно стрелке в этой веп рис. .А.17,б,в). то Ct=-dfc. При закорачивании ветвей d, , £ граф и дается в точку, поэтому Д=1.

Для нахождения определителя системы А закорачквием узл1 питания от источника э. д. с.) и получаем грпф рис. А.17. а. От г ходим к графу рис. А.17, Й.

Для вычисления А графа рнс. А.17, д воспользуемся ]

Гутйм ыещду зачерненными точками. Между этими точками два пути: первый по вегаи с, второй-во ветвям {а+с}, tb-i-d). Поэтому u=i?((i4.c+6-bdl+ + {a-i-cH6+d)-l. Таким образом.

W.± eb-dec .

(А.5

Длн определения передачи схемы рнс. Л.17, а по напряжению менаду вход иой ветвью (ветвью с источником э. д. с. между уаками tn и п) и выходной (е воспользуемся тем, чго выходное напряжение на зажимах ветви е равно току /,

этой ветви, поделенному t

а рве. A.l-,

Определить передачу

а проводимость. Следовательно, зменеиня произойдут в

вычислениях, если яа тока (рас. АЩ. току к ветви е и отношение ннаряжения на выхаде (на ветви с) к входному току. Вы; прежнему является ветвь е, но ней проходит ток /в(л- Положительное напралленне для прохождения по этой ветви то же. что н в примере 173.

Решение. В отличие от примера 173 входной величиной яйляется теперь яходиой тск /в,-Поэтому

iBb,jfBx=Cr&rit- (А.;

Числитель правой части (А.26) такой же, ка(. числитель правой части (А-25). Определитель Д в (А.26) отличен от определителя в (А.25) эа счет того, чго для (А.25) оп подечитывадсн прв питании схемы от источника э. д. с, тогда как в рассматриваемом случае оп должен быть подсчитан прн питании схемы от источника тока. Длн подсчета в этих условиях ветвь с источннгаж тока следует считать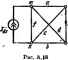

Поэтому

ь для этого случая был подсштав равее (си. форилу

м (a+d-f/) cs+rt-b6e)+№f{*+c)+a/(&-H -f4f(c-j- )-j-u -

Отношение выходного

а ретви е к входному току

1P+d-i-f}{M-i-cb-i-be)-i-adlb-i-t)+a}ib+e)+df{c+ei+adt

предел№ня входной проводимости схемы, числителе {А.21) должны быть учтены все п (путь через источник э. д. с. исклю ЭДНОЙ проводимости схемы рис. А.19.

ся от Цветочника I пути между уэ- Так, например, пря

, ..- . ---------.- штеле (А.21)долж

быть взято четыре слагаемых, так как возможны четыре пути меиаду уэлэмв

в л (pic. А.19. 6-di:

А &+*ИйТГНа+ё+{а+7 -

Все в числителе взяты со знаком плюс, потому что направлевя! всех четырех путей взяты в ввде продолжития но часовой стрелке направления вход-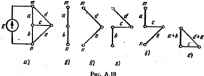

J!! О перелет, по ms, в iBolHoi. Т-иосте (рис. кИО, dl. ST , сготвва тока / . Выюдно ветвью иыяетси ветвь е. По ней протекает ток 1. положительное направление которого ноквзапо стр1укой.

t т I 3

4,1,3

п,2,3,п

) 1)

Рис. А.20

y,JS!TT?%2 iJ- ° ° Р ветви евд

5. иГс и 1st i * -

Пмгра(и пик путей иаовражены на га же рисунках. В результате полу.ии oig(H-e4-d)+bg)o+c+i)

>№+Д?+( 1Д(с+<!)+(с+Ое1+ -

+o (t4-e+dl+l.4g(o4c+B

§ Д.18. Сопоставлекне Bi

денных н ненаправленных гр ций, прн проведении которы:

влеииых н ппквправленных графов. I. Б наирав-к расчет состовт вэ простых и наглядных опера-а вероятность ошибки.

2 По сравнению с обычяымн алгебраическими иетодамя решение системы уравнений прн помощи графов может дать некоторую экономию времени.

3. Прн сосивлеиии определителя огстемы ненаправленного графе отпадает необходимость подсчитывать взаимно уничтожающие друг друга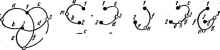

Ю 6) г) д) е)

Рис. A.2I

нри раскрьпни I

о методу узловых потенциалов.

[ матрицы проводимосте*

4. Преимущество иаправленаых графой пщлр. вен, хождения передачи по (А.4). Однако, поскольку граф i

нынн-> простота

нахождения передачи по (А.4). Однако, поскольку граф в готовом виде не задан, жно построить граф и подсчитать передачи его ветвей, енмущество сенаправленных графов состоит в том. что ие требуется

. . никаких уравнений и строить граф (так нак графом является сама

электрическая схема); однако определение передачи но (А.21) требует несколько большего времени, чем иримененне (А.4).

ПРИЛОЖЕНИЕ Б

МАТРИЦЫ В ЭЛЕКТРОТЕХНИКЕ

§ Б.1. Основные свойства мн1рнп. Матрица-это совокупность величин, расположенных в виде прямоугольной таблицы. Чтобы отличать матрицу по внешнему виду от определителя, ее заключают в квадратные скобки [ i нлн в двойные пфтикальные черты .

Каждый элемент матрицы часто снабжают двумя индексами: первый соответствует номеру строки, второй-номеру столбца. . ,

Матрицу называют кеадрааиюЁ. если число строк в ней равно числу столбцов, например

Oji aj OisT оц aj /.J= Oaf ва =- Oaf 23

Диагональной называют матрицу, у которой равны нулю, в все остальные- нули, например

главной двагоявди, равны

Матрицу, у которой элементы, расположе единице, а все остальные-нули, называют единичной, например

[11 =

Неопределенной называют матрицу, в которой сумма элементов любой строки н любого столбца равна нулю.

Две матрицы равны, е У равных

в равны соотвегс а матрице

пствующие

J лементы этих матриц. Так,

примера й,1Йяз- де пе следует ра-

Операцни иад матрицанн (нх сложенпе, умножение) постулированы нз сооб-ражений рациональности. Прн сложении (вычитании) матриц следует сложить

У равных матриц равны определители. Для рассмотренноп - 0i,O]j=frjjbjj-frjjbji, но из равенства двух определителей i самих матрии.

Гцни иад мат рациональное

(вычесть) соответствуюпще элементы sthk матриц. Например,

Умножение двух матриц (число столбцов первой должно бьЛь равно числу строк второй) производится по правилу -строка первой матрицы умножается на ft-столбец второй.. Для иллюстрации этого правила умножим две матрицы, эле-ментами которых йвляются числа:

-5-2.7 1.6-J-2-81 5-4.7 3.6-J-4.8J

Руководствуясь приведенным правилом, нетрудно убедиться в том, что \А\ [В] [В] (AJ, т, е. результируюспэя матрица ззнисит от последовательностн расйолоЖ1Шия матриц сомножителей.

По отношению к матрице {А], ели определитель ее не равен нулю, можно составить обратную матрицу \A\-K JVia этого необходимо: а) квиедый элемент исходной матрицы [Л] заиенить его плгебраическим дополпшием; С) транспониро-ю матрицу, т. е. строки еделать столбцами; в) разделить транспо-

рованную матрицу и Пример 176. Пусть М1=Г

ь исходной матрицы \А\. . Определить [АуК

Решеине. Заыенва элементы матрицы ш алгебраические дополнения,

мнметьГ

И матрицу Г Л. После транспонировании буде L-

Г а.

Прои!

------ н MJ[B]=q отиосительнматриныШ следует обе

Ы) при

Для решения уразвелня (..... . ,

- этого уравнения умножить на (Д-1.- M- HlIB=(.Sl- fQ и учесть, ч Получни [В=1И-(С].

столбцы в матрице

М1-ЧИ1 = 1. Получни [В=1И-(С].

[ уравнении [A][X\=Q Можно

е страд в матрице Ij.