Передачу петлд обратной связи часто оботначают Г с индексом. Передача петли йратиов связи равна проваведевию передач вег !В. образуи)л1вк яу петли. В графе из ряс. A.I3 три петли обратной связи: первая петля с Г,=Л. вторая с T.=lg, третья с r8=Cii.

OsISh формула для определения передачи графа О аапясываегея следующим образом;

А РА+Р.а.+...+ Р.й.

где Рь-передача fe-ro прямого пути ог истока к стоку; и-число прямых путей.

Определитель йь равен единице минус сумма взятых поодиночке передач петель обратных связи!, не касающихся Ai-ro прямого п>ти (но эти петли отут i друг друга), плюс сумма попарных произведедяВ передач

1 обрат-

: сумма попарных г---.-----.....г-........- -г--.

1эеЙ, пе касающихся друг друга и к-го прямого пути, минус сумма троимого произведения петель обратных связей, не касающихся друг друга н fe-ro .прямого пути, плюс и т. д.

Определитель Д равен единице минус сумма взятых поодиночке передач петель обратных связей (касающихся и ие касающихся друг друга) плюс сумма попарных произведений передач петель обратных связей, пе касающихся друг друга, минус сумма тройных произведении першач петель обратных сввэЛ, не касающихся друг друга, плюс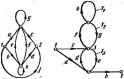

Прим> 171. При мулу (Л.4) к графу рис. A.IE

Гсшенне. Для первого прямого пути с передачей ft= = ab определитель Д равен еда-

Рис А. 12

Рис. А. 13

этого прямого пути (Ti-i-TJ/, плюс попгфное произведение передач петель сб-ратной связв. не касающихся друг друга н выбраним-о прямого пути.

В графе рис. А.13 отсутствуют петли, которые бы не касялись друг друга и не касались первого прямого пути. Поэтому слагаемые с попарным пронэтепеннем передач петель обратной связи, как и взятые по трое (и более), в выражении

-.-. . . 7-a=fe.

Для второго прниого пути P=ce}: Да=1-7,-Зпдаекатель A=l-(r,+rB-t-ra)+TiTs; Tj,=ed. В выражения для Д вошло произведение а Г петель графа. Таким образом.

§ А.6. Вывод формулы для пгредачн графа *. Положим. . узлов. Для любого (ft-ro) узла справедливо урмнение

двух несопрткасаюшихся .

При первом 41 I о А. и др. Hai

и § А.6 можно опустить. Идея вывода взята i аенные графы, Энергия*. 1961,

Обозначим протодвмость ветви, соединяющей проия

иоозначим прюодиыость ветви, ные узлы / и ft. через /д. Матрвна

*и (в, ... я1 <я ...

h V о являются производные

графа

0б1>аз1 имеет

. зыбран-Еорцдой в:

(AJ}

Все злеменга .строки будут пулями, еслн -независимая nepeweni Матрицу.столбец. составлепный вз переменкыл *i, .....х , обозначим [Х];

rXi -!

<A.tD

(Д.9)

Единичную матрицу порядка и назовем Щ: О С..01

Обозначим матрицу-столбец ....... ..нл пений, выражаемую графом, запнсывакгг так:

О ... О .0 О О ;.. I

переменных ф,=*й-f,. Систему урав-

(;-Пт-[Ф1. -!-<., -( ... -Wl

Введем систему уравнений, матрица кшороЯ Л1=(/-Г];

012 п ... ai и Ом ... Ом

(A.II)

(А,12) I

(Д.13)

№ линейной алгебры известно, что определитель Д-матрицы i сан следукщим образом:

(А.14)

Каждый член суммы содержит п множителей. У кавдого множителя имеется по два индекса. Петвый индекс соответствует строке, второй-столбцу; /-число

инверсий чисел I, 2. ..., п в последовательности обозначений а, р, v..... для

первого индекса; /-число инверсий чисел I, 2, ...,пв последовательности обозначений а, р, v, .... я для второго индекса.

Напомним, что инверсней индексов называют такое чередование индексов, при котором /> . При подсчете общего числа инверсий данного (например, первого) индекса нужно дожить все инверсии, которые образуются при переходе от нсхсдаоб цифры этого индекса ко всем послсдукщнм. Так, положвы. что ка-кой-то индекс, например первый, имеет чередования 461352. Так как за цифрой

н следуют цифры /, S, 2,

4, то это дает первые

три инверсии. За цифрой € вахолятся четыре цифры: 1, 5. 5. 2, ыеньшпе 6, что дает еще четыре инверсии.

Все цифры, стоящие справа от /, больше единицы, поэтому по отношению к ивдексу / инверсии отсутствуют. За цифрой 3 находится цифра 2-одна инверсия; за цифрой 5-цифра 2-еще одна инверсия. Итого в последовательности 461352 имеется 3-}-4-}-1 + 1-9 внверсян.

Вспомним также, что замкнутой последовательностью двух индексов называют такую последовательность индексов, в которой второй индекс у последнего члена принимает то же значенпе. с которого вачал изменяться индекс первого

X замкну-

(АЛ5)

(А.16)

Запишем возможные комбинации чередования индексов, образую le последовательности:

if. Ik. kl. Ix.....yp. pi;

if, fi.....лот, mp, pn.....gu, ..., Iq.

В комбинации (A.I5) замкнутая последовательность образована ми. Первый индекс изменяется со значения i, а второй-со значения /. Посяед< ательность является замкнутой, так как у последнего члена второй е (, с которого начал изменяться индекс первого

1нвёрсий первого индекса, /-ч1

членв. уже гжорнлось, 1-% версий второго нндшса.

Для последовательности (А.15) число инверсий второго индекса на л-! больше числа инверсий первого индекса. Действительно, первый индекс в (А. 15) имеет нуль инверсий, второй индекс претерпевает -I -инверсий, поскольку более старшие индексы /. А. I, х, .... р (нх число равно и-1) расположены до младшего индекса . Следовательно, Г~1=п-1.

Миожителн в чередовании (A.I5) разделены иэ k групп. Первая группа состоит нз di=2 множителей; вторая группа-из йЗ множителей; последняя *-я группа-на *+1 множителей. Число всех множителей в (A.I6) размо порчдку определителя, т. е. разно л. Поэтому ((i-J-da-J-d2-J-...-J-dft=n. Для каждой группы множителей справедлива формула /-/=d-I. Определим, насколько различаются / и / между собой для всей последовательности (А.16), южяощей k групп:

l-idt-l+d-l+ik-l+..+d-l = /=/+л-А.

В произведении типа (A.J6) могут быть множители, имеющие одинаковые индексы, например тт. Каждый такой множитель можно рассматривать как группу, состошцую яз одного члена. Для такой группы d=l н /=/==0, т. е. для этой группы выполняется то же условие /=d-I, что н для любой другой группы в (А.16).

При определении знака каждого слагаемого в (А-14) следует учесть, что прн любом числе k инверсия в 2k ие скажется на знаке, так как (-1)2*=1. Поэтому в правую часть (А.17) можно добавить 2k. Тогда

/=+n+fe- (А.17а)

Распространим полученный результат на определитель матрицы {A.I2). При -раскрытии определителя матрицы (А. 12) имеем дело с произведениями множителей даух типов. Первый твп множителя-вто ] =1; второй тип произвепение л отрицательных множителе вида -li/. Таким образом, для матрицы {А. 12) знак перед каждым слагаЬмым определителя зависит от знака, произведения (-1)1) . т. е. знак, перед каждым слагаемым второго типа определяется значением 1+1+п. Но с учетом (А.17а)

( )-h+ =-l)+++b-h =( l)=(+ )+*=( i,fc. (А.,8)

Следовательно, знак перед калщым слагаемым второго типа определяется числом групп ваыкиутых в нем гюследсввтелыюстй.

Множители второго типа могут быть неаяхлькихразновидности.

Первую разновидность образуют замкнутые последовательности типа (A.I5). В каидюй из них только одна последовательность чередовании индексов (ft=l). Поэтому перед каждым слагаемым aroft разновидности в соотвегсгани с (A.I8) следует поставить знак минус.

Вторую рвзновндность образуют произведения множителей в виде двух замкнутых последовательностей чередования индексов (А=2). Перед каждым слагаемым этой разновидности должен быть поставлен знак плюс, так как (-1)*=.

Третыо разновидность образуют произведения множителей с тремя (fc=3 замкнутыми последовательностями чередования индексов и т. д. Таким сЛазои

Положим, что выходным а входным-сигнал jc первого узла. Воз; Для нахояадення х составим выраже

выходной сигнал второго узла xg, узлы равны вулю.

oli xi ой ... ч

(A.I9)

Разложим числитель (А.19) иа слагаемые. Каждое и ровки множителей имеет вдд

и может быть изписано в виде

ХаР*Д*.

, где xi-входной сигнал; Р-Щ

,----- - . , ----- ие множителей, у которых первый ивдекс

у потвого множителя 1, а второй индекс у последнего множителя 2.

Следовательно, представляет собой пч)едачу прямого пути иэ узла t в узел 2; представляют собой множители, которые иэ содержат цифр и 2 индексов входного в выходного узлов) и всех цифр, встречающихся в ивдексах у множители Pfc.

После перегруппировки множители Л* представляют собой замкнутые последовательности, у которых первый индекс первого множителя и второй ивдекс последнего множителя одинаковы.

Это означает, что все представляют собой передачи азмкнутых петель, не касающихся прямого пути Рь кежду входным и выходным узлами.

Окончательно

Xi=Xi

(А.20)

Формулу (А.201) в литературе иногда :

аграфы

§ А.7. Ш. .. собой топологическое изображена этого графа соотаетствуют ее узлам

жиый граф представляет 1 схемы. Уалы и ветви оправленных графах i

г. &ойства ветвей характазую

шеы обозначены латинскими буквша а, Ь, с, ... Поскольку каждой i ..

электрической цепн соответствует иекоторан дуальная ей цепь, то кахщому вена-

ому графу, соответствукац

сгфепгшовать дуальныв еиу граф. Прн работе с НОЙ являегся формули

жой цепи, иоже1 1ньши графами основе

Правая часть (А.21) по структуре полностью аналогична формуле Мэзона (А.4) для направленных графов.

Формулу (А.21) используют для нахождения входного сопротивления (вход-вой проводимости), взаимной проводимосга ветвей и др.

Здесь /-ток, цротенаняций по некоторой выбранной ветви графа, по отношению к которой и определяется входная или взаимная проводимость**; Втд-напряжение (ток) источника- питания схемы, присоединенного зажимами к узлам т н я; С,-произведение проводныостей ветвей пути мегкду узлами тип, проходящего по выбранной ветви; Д-определитель для системы, полученной на исход.

ветвей выбранного пути С,; Д -

мой прн коротком замыкании {эакорач определитель исходной электрической с

Число ч узлами т и

енов саг 1 графе. В

(А.2) рнано числу возможных путей между не входит путь ст m к п через источник пита-

г быть получен t

(атрицы проводвмостей I. Однако такой способ

ветвей схемы, составленной по методу узловых . .

подсчета Д довольно громоздок и трудоемок. Дело в том. что при вычислении Д путем раскрытия определителя упомянутой матрицы пришлось бы иметь дело с большим числом слагаемых, часть которых имела бы одинаковые абсолютные значения, но разные знаки (эти слагаемые соответствуют так называемым избыткам в каждой строке определителя).

Подсчет Л, прн котором не возникает взаимно уничтожающих друг друга слагаемых, осуществляют путем вычисления его как суммы величии всех возмож-1П.[Х деревьев, которые могут быть образованы для данного графа. Под деревом понимают совокупность ветвей, которые касаются всех узлов, но пе образуют ни одного замкнутого контура. Остальные вегвя графа, пе всщедшие в ванное дерево. называют-хорЗалы. Для простейшего графа рис. А.14. а сказуемые деревья показаны на рис- А.14, б-s.

Величина дерева равна произнеденаю проводимостеЯ ветвей этого дерева. Величина дерева рис. А-14. б равна аЬ, дерева Л.14,-в-*с, дерева рис. А.14, г- ос. Определитель графа рис. А.14. а Д=аЬ+ос+Ьс.

§ А.8. Определение числа деревьев графа. Для определения числа деревьев гра положим, что проводимость каиадой его ветви равна единице. Тогда все ветви канздого дерева буд)т иметь проводимость по 1 и величина каждого

е С,й, -

обозначают и няаче, например рДд {см. формулу взведение обозначают как Pj, то слагаемые определителя знаменателя формулы (A.2I), т. е- слагаемые Д, обозначают как РД. * В общем случае роль / в формуле (А.21) можег выполнять пе только ток.

(А.20)1 илиРД. Ееднэ

дерева также будет равна 1 (произведение единиц равно единице). Если в рассматриваемых условиях для исследувюй электрической цепи составить матрицу узловых проводимостей прн люби* заз(шленим1 узле этой цепи, то численное аначение. отредештеля этой матрицы будет равно числу возможных деревьев графа.

В качестве примера подсчитаем число деревьев для графа рис. А.14, а, положив а =(>=£= 1:

о малоч

Хотя sHSime числа возможных деревьев и полезно, t расчета, так как деревья еще иужно составить и опрщ дерева. Для относительно сложных схем отыскание i

ваегся делом довольно утомительным и потому иа практике примекиют упорвдо-

:пособы определения Д, которые рассмотрены и § А.9-А.11.

§ А.в. Разложение определителя по i

которому узлу S подходит п ветвей с проводт* пель раскрывается но узлу при помощи формулы

н fli, Яа, .... а .

t=e,ki-i-a,ai&t,+j}a)aia !ljk+...+aiaiat...a \,f,, , (А.22)

гае 5]aA=Mi+Mi+Mi+..Aft- отфеделнгеля исходной схемы Путем занорачяван остальных ветвей, подходящих к узлу этого уэла;

(блитель. получающийся вз 1етви Яд и исключения всех коде всех остальных ветвей

Даг-определитель, получающийся в.

В J

определителя исходной системы прн одно-я, и исключении из схемы (холостом ходе) узлу s;

юей, подходящих I, получ;

Ai/fc-определитель, получающийся из опредеянтеля исхрцноа схемы при одновременном закорачивании ветвей t, j, k и исключении (холостом ходе) всех с ветвей, подходящих к узлу s. по которому производится разложение.

Множитель Aj . у последнего слагаемого правой части (А.22) npедcтaвJ

й при одновременном закорачивании всех ветвей, подхо-

собой определит дящих к узлу s

§ A.IO. Разложение определителя по путям между дщмя произвольно выбранными узлами. Прн разлонгении следует выбирать узльЕ. по отношению к котм)ым схема в геометрическом смысле наиболее симметрична. Это упрощает подсчеты. Разлйжение определителя Д по этсму методу производят прв помощи фсфмулы

.A = 2]Pftflft. (А.23)

где Pt-произведенне провоцимостей-. ветвей *.го пути между выбранными узлами; Aft-определитель А-го пути, подсчитанный по схеме, полученной иа исходной прн закорачивании ветвей, по которым проходит *-й путь.

Пример 172. Найти определитель Д даумя методами для одной и той же мостовой скрещзНЕОй схемы рис. А.15, п..

Решение.. Сначала определяй Д путем разложения по узлу /. К этому узлу подходят три ветви \а, d, / вместо й(. Oj аъ (А.22)1. поэтому

й= д-d4(-J-д-яд-J-йdд-J-dДrf.-йд.

(>ределитель Д находим для подграфе .рис. А.15, б. Он по;

ген из графа

. - путей закорачивания ветви я и размыкания ]

=се-\-сЬ+а> (попарное протэвенение 1ф1жодимостей ветвей см. § Для опрв-деления 4( служит рис. А.15, в, для оприелення Ду-рис. A.lS, s; Саа=1=1а-