Передача ветвя может иметь размерность нроводимостн. сопротивлеиин иле пулевую размерность.

К тону или иному узлу графа кроме входного н нлходвого в общем случае ыожет подходить в от него ыожет унодить по нескольку ветвей. На рис. А.1. б в качестве примера изображен некоторыЯ граф с узлами Q, I, 2, 3, 4, 5, 6. Передачи вегвей этого графа обозначены букваыа а, Ь, с.... Направление передачи указано стрелками.

Под X] будем понимать уаловой сигнал первого узла, под Xj-узловой сигнал второго узла и т. д.

Уаловой сигнал А-го узла равен сумме сигналов, приходящих к t-му узлу. При составлении узлового сигнала k узла выходящие иэ А-го узла - сигналы не учитываются: оти учитываются гри составлении узловЕлх сигналов тех узлов, ч которым этн сапгалы подходит.

Так, узчшой сигнал первого узла графа рве, А.1, б. JCj= 1 .Хд+х второго эла Xtbxt-xt,: третьего узла Xj=fiXf н т. д.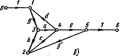

Увел графа, и

В собой величину, принятую в

... .- - . ---- ----- -.,. -----,---------ой системе ва

входвуго, овлчио изображают иа чертеже слева а узел гри, соответствующий выхадяой величине,-снрава.

Првиято так изображать граф, чтобы от нходного узла отходила только одна вегвь, в подхояящня ко входному узлу ветвей вообще ие было.

Аяалогичио, к выходному узлу должна подходить только едва ветвь (отходящих от него вегвей ие должно быть). Это можно сделать, введя в граф дополнительные узлы и ветви, переаачн которых равны едиииие. Так. в грак рис. A.I. б дополнительными узлами являются узлы 1 я 5. Между входным узлом О в дополнительным узлом / имеется ветвь с нередачей 7. алогично, дополнительный узел 6 соедниен с выходным узлом 6 ветвью с нерелачей, равной I. Часто узлы, гереаача между которыми равна еднинце, бозвачают одинаково. Так, например, для схемы рнс. А.1, б узел О можно назван, узлом 1 (тогда па рисунке будет два уэлэ, обозначенных пвфрой 1).

§ А.З. Пьрехоя от изучаемой системы а ваправлеииому графу. Дли того чтобы от изучаемой системы, например какой-либо алектрической цели, перейти к соответствующему ей направленному графу, применяют различные методы в аавнсимости от того, каким обравом записывают ураввения для этих цепей: на основании аяконоа Кирхгофа, используя -метод узловых погешшаиов ели метод контурных *оков и т. с.

Напраы; ныЙ граф содержит ту же нафорыацию. что п снстема уравнений. Только внформацнв эта вырвжеяа графически.

Еслн ва основу взять уравнения, составленные па основании применении наконов Кирхгофа, то узлами графа являются токи ветвей и напряжения на эле ментах схемы.

В том случае, когда за основу взяты уравнения, составленные по методу узловых погекциалов. узлы графа будут выражать собой потенивалы узловых точек схемы и искомые токи (нтряжснии).

даже ие ааписывап сами ураввения.

При некотором навыке rpL иослужавшие тсвовой для его

.аф вычерчиваю] J состйвлевия,

Упорядоченный переход от заданной

схемы к ианразленвсыу положив в Основу

графу, . у -с= yZ, S l ОТл ко гур ГОК, ( ереюд ркс. А.2 к ркс Д.З.

Направления контурных токов во веек онтувяк выЯнпа.и п. . .

Каждому контурному

каждой

выходвая величина, выходной величине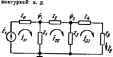

рнс. А.2,в крсЛ три куркГ* тока 1ц, /gj и /дз, одна контурная э-д. с. и выходная неличнна~ток соответствует граф рвс. А.З. я, в котором имеется пять узлов

Узлы /м располагаем в серединах соответствующих контуров, а узлы И узел Быдоднон величины выносим ва нернферию рисунка. Со-единяем нарисозанные узлы ветвями,

указываем на икх стрелки и запи- p f. а 9

сываем звачения иерч ветвей. Каж-

SLltli* ью с передачей fcfts=l/ZM, где 2-

5 ,ГзнГеТ.1Г* *3- iS = направлена кулу

х=~о- ~ fpo зНл-за

,-o;Tyj.> .fe :LpSrs=o.a ryfлyT; ff-sia

bpk=ZkpfZp. гт 2рр-собственноТсоп. ротивление р-контура.

Гн согласном паправленим всех кон-турных токов пч едач всех вегвей между уэланн i и р положппльиы.

По методу узловых потенциалов граф строят так же, как и по методу контурных toKOB. толида узлами графов ляются потенциалы узлов схемы, узловые токи и выходная величина.

Если в элжтрическоН схеме узлы А яр соединены ветвью с проводимостью Ykp. а суммарная проводимость ветвей, сходящихся в узлах * и р, обозначена соответственно через У и Гр, то на графе между узлами и % ёудут две

,Л.НарутоГс;.глкГна Г.?е.П 4УГ

Рнс, А,з

№и (рис. А.З. б). На одной

Бюлиани, , , то ереый иядекс у о yKMbiBanjsui, кетороиу

oJoiBcicTsyer у1ел в£да лн Х М уала 4 к ум, д и графе

од>?лГ4 и?грГ Tj/f

t (( т а.я Bocmwwwao тока, то комплексное сопрогнв-

должны

этих

ление Z JerlZrv.: JiZ тока, го комплексное сопрогнв-/гаие слвдует вамекить ва актнвное етриявление Я. коиплексную npS oAH.

ь г-Hi

гочкн над ф, Е, I, сввдетельетаукщне и неличин во времени, не ставят.

о синусоидальном характере i , . . ., ..

itpHM 169. Со.ставнть граф для лестничной схемы рис. А-2, считая входной

величиной э. д. с. £ и выходной ток /g-

Решенне. Граф рис. А.З, о составлен по методу коитурвых токов для

уравнатий, записанных в комплексной форме:

-/as (Z,+Z +Zs) -0: Передачи ветвей иа рнс. АД, а обозначены:

Пример 170.

6i,= V(z +z,): ft.,

Z,+Za+Z =

2i .

Zo+Z,-

*аз =

к узлу h равна 1, так Kfflt /j/sj. . граф для схемы рис. А.2 на

Решение- Обозначим: Kel/Zo, YiVIZaX =1/2; > = 1/(z4-.и =>o+*i+>a; >и=>в+>8+**в- Запишем систему уравнений:

На рнс. А.З Ciil/rib th,=YiYn=YtfY-ii

Предполагается, что не равен нулю ни один а энвиеиа1елеи выражении ору *рь. Oftp, Ops длн значений параметров схемы, находящихся в рабочем диапазоне.

Порядок расположения узлов на чертеже можег быть любым (о расположении узлов входа ------

т быть любым ( I выхода уже говорилось), однако рексмендуется э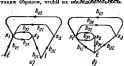

ла фектическому прохсщденшо сигнала (наформации) от входа к рыходу.

и от того, ка-гбраны в ка-узлов, для одной и той !т различную

фуктун

летим, что г имеется ш

эуются принципом определяют выходную величину для графе, в котором сигнал действует от первого источника, затем определяют выходную величину для графа, в котором сигнал действует от второго источника, и т. д. После этого, суммярунэт ныра-жения для выходной величины. Однако можко поступить и иначе, а именно: граф с несколькими источниками сигналов одинаковой частоты свести к графу с одним источником (рис. АЛ). С этой целью один на сипгалов, например сиг-нал £ на рис. А.4, а, примем за базисный. Узлы остальных сигналов (в примера узел тока /) объединяют с базисным, так изменяя величины передач от этих узлов к остальным, чтобы сигналы, подходящие к ним, ocrajmcb неизменными.

В рассматриваемом примере oбъeдиняei. узел 7 с узлом £ (рис. А.4, б) и изненяем передачи и bj на и исходя вз условий bEbjl. bE = = bj. Отсюда bbjlt. bbffi.

Когда граф составлен, его используют для определения передачи от истока к стоку. Входной снгпал называют истоком, выходной-стоком.

Определение передачи графе производят двумя способами: 1) последовательным упрощением его путем применения правил, рассмотренных в. § А.4; 2) прн-ыенением общего юраженвя для определения передачи направленного гпа*а (правила Мэзона)-см. § А-5. Возможен и промежуточный путь, когда граф частично упрощают, а затем применяют это правило.

§ А.4. Прав

шьзуемые для упрощения направленных графов. Позна-с операциями ко упрощению графов. 1. Передача послвдоватеньно соединенных ветвей (рис. А.5, о) равна произведению передач этих ветаей (рнс. А,5, б). Действительно, jtg=oxi, xbx. Под-сгавни в последнее выражение вместо х его эквивалент из предащущего, получим хз=оЬх1.

Рис. А.5

2, Передача наух параллельных, одинаковым равна сумме передач этих ветвей (рис. А.5, в, .

Рассмотренное преобразование не может быи ветвям, стрелки на которых

Образом направленных ветвей

--- ..... е распростри

3. Устранение простой узловой называть точку графа, к которой в общем случае подходят

рис. A.S,

Условимся простой узловой точкой (Которой уходят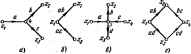

Рис. А.6

I ветвей и которая не входит

выми точками на рис. А.6, а, в являютс

рис. А.6, а

Xiaxi; xtbx£ X(=gk*.

обратной свнзи. Простыми узло-гственко точки 4 в 5. Для графа

Xfiabxii Xfi=acxi. (A.I)

Граф рис. А.6, б эквиаалентея графу рис. А.6. о. Глн графа рнс. А.6. в x=axi+cxi; х=Ьх=оЬх1+Ьсх£ x3=dXi=adXt+dcXt.

Граф рис. А.6. г эквивалентен графу рис. А.6, е.

4. Устранение контура иа пути. Граф рнс. А.7, а имеет ветвь с передачей с меяаду узлами 3 и 2. Контур,. образованный вегвя! вают контуром на пути (контуром в пути). Просгейщнми Преобра

контур иожно устранить и граф свести к рис. АЛ, б. Для графа рнс Л.7, а

Ха=иЬх1+ЬсХз. . (А.2)

Следовательно,

Ветвь, выходящую из i

будем называть петлей. Петля Ьс из рис. А.7, б соответствует слагаемому Ьех правой частн равенства (А.2).

Рнс. А.7

Рис. А.8

S. Исключение гетли. Граф иа pnt. А.8. о имеет петлю с передачей с. Эту петлю можно устранвть и свести граф к изображенному на рис. А.8, б. Действительно, для графа рпс. А.8* а можно написать

Xi=axi+cxz xz=bxi. Из первого уравнения ьиходвм Xz=axi!{l-i и, подставляя во второе, получаем

.с<1.

большего числа петель одной петлей. Петли с передачами 6 одной петлей рис. А-9, б с передачей Ьс. Эта вытекает ва следующих преобразо-ваиай для схемы рис A-S, я:

[6*е Xt=axi+bXs+cxz=

= axi+v>+c)x.

. Схема рнс. А.9, 6 удовлетворяет этой строчке.

7. Удлинение (растяжение) узла. В некоторых случаях при преобразовании графов оказывается полезным удлинить (растянуть) узел. Положим, что требуется удлинить узел 2 графа рнс. А,10. д. С этой целью: а) узел 2 подразделяют на два узла (рнс. А.10, б): ва старый узел 2, от которого отходят те же ветви, чТо и в первоначальном графе, и иа новый

узел 2. к----- -------------------------------

к узлу 2;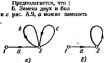

Рнс. A.S

е ветви, которые в исходном графе подходили

Проверим справедливость преобразования. С этой целью для исходного гоафа рнс. А.10, а запишем узловой сигвал в узле 2:

Xi=axi+cxt.

Узловые свгизлы узлов 2 в 2 графа рис. А.10, б

. xJ=flXi-}-CX4 и Xj=.xJ.

Таким образом, узловой сигнал в узле 2 остался без изменений. Не изменились и узловые сигналы в остальных узлах графа.

Рассмотрим два примера иа опрепелеиие передачи графов путем-последовательного упрощйиия.

Первый пример иллюстрирует рис. А.П, о-9, второй-рис. А.2. Положим, что верхний в нижняя петлн g к h рис. A.I2 oTiTCTByioi в только петля е}.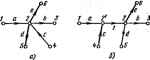

Составим передачу от узла / к узлу 2: l-ej

Учтя наличие верхней и нижней петель и поделив соответствующие члены а (l-g) в {1-А), получим

ДС . bd , td+bec

. , -e*i-ft (i-ft)<i-e)

*-(i-fi)1i-/.j

§ A.6. Общая ффнула для цередачи графа. В 1956 г. Мэзон предложил общую формулу для определении передачи графа. Эта формула является основной при расчет графов. Прежде чем перейгн к неП, познакомимся с яекоторыми новыми понятиями.

примой путь Р-это путь вдоль стрелок от истока к стоку, прн прохождении которого ни один иэ узлов не встречается более оД-вого резв.

Передача прямого пути равна прсязяедевию передач ветвей ©того пути.

Между истоком и стоком графа может быть несколько прямых путей. Тик. например, для схемы рис. А. 13 мещду истоком (узел 1) f+iZF, в стоком (узел 2) есть два прямых *

пути. Первый прямой путь-это путь по ветвям с пе1)едачами а и Ь, Передача этого пути Pt=ab, ВторомnpfiMofi путь-это путь по вмням с передачами с, е. Ь. Пере, дача его Рх=сеЪ.

Нн один из других возможных путей от узла / к узлу 2 в этом графе не относится к категории прямых путей. Например, путь через ветви с, /, g, *, b не являетсч прямым путем, так как на этом пути узел 3 встречается дважды. В обп№Й формуле необходимо учитывать твкже передачи петель обратной связи.

Петля обратной связи представляет собой замкнутый пул, вдаль которого (Щ1 жругу) каждый узел иомет встретиться только во сщишу разу.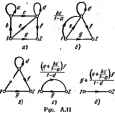