в 1873 г. английский ученый Джеймс Кларк Максвелл обобщил й развил иден Фарадея (см ч. П1 учебника). Он показал, что явление электрЬмагнитной индукции наблюдается не только в замкнутых проводниковых, но и в замкнутах непроводниковых контурах.

а д. е.. наведенную в проводнике длиной dl, пересекающем магнитные силовые линии неизжнного во времени магнитного поля, часто определяют по формуле

где rfe -э. Д.С., наводимая на участке прсеодника длиной dl; v - скорость перемещения проводишка относительно внешнего магнитного поля.

В формуле J2.4) индукция В скалярно умножается на векторное произведение dt н v. Если в результате расчета по формуле (2.4) э. д. с. окажется положительной, то это означает, что э. д. с. de направлена согласно с положительным направлением элемента проводника 2?.

Формула (2.4) в одинаковой степени пригодна для определения э. д. с. при движении проводника в неравномерном и в равномерном магнитном nojiHx, если ма1-Н1Гтное поле неизменно во времени.

При движении проводника длиной / в равномерном неизменном ео времени поле э. д. с. удобнее определять по формуле

e = Blv . (2.5)

где В -индукция внешнего равномерного поля; /-длина активной части (проводника (nepL-ce-кающей магнитные силовые линии); и -составляюш,ая скорости движения проводника, нормальная (перпендикулярная) магнитному

nOJHO.

Направление наведенной э. д. с. лри использовании формулы (2.5) определяют 0 правилу праюй руки (известному из курса физики): если расположить правую руку таким образом, что магнитная индукция входит в ладонь, а отогнутый большой палец направить по нормальной составляющей скорости проводника, то возникающая в про-водшше э. д. с. совпадает с направлением четырех остальных вытянутых пальцев правой руки.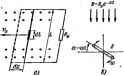

Рис. 2.2

Из формулы (2.5) можно получить формулу <2-1). Пусть шра ----------поле, ьаправленном герпенднкулирно рис. 2.2, о, геремещ

водник длиной Л Являю.цнйся составной частью некогорого коитура. Нормальна! полю сосгавляквцая-скорости движевия проводника v =dxlul, где л-координата

в иаправлений v . В стре31жпрс щника длиной / наводится э. д. с* которую лпределим в соответствян с формулой <2.Б>: de=Bv ul. Э. Д. С. в проводнике длиной/

Г оиэвевеняе dxdi лрелствелиет собой элементарную площадку dS, лроннэывае иую магнитным потоком. Приращенве потока в контуре d®=Bd5. Таким обра-эои, числовое значение s. д. с. авко ёФ/Ш. Имея в виду, что положительное направление для наееденнвй э д. с. в положительное направление линий В при воэрастанви потока связаны правилом правого винта, получим при ш= I

Возникновение 9. д. с. в проводнике, движущемся в магнитном поле, noHciraii, используя понятие о силе Лоренца. На электрический заряд q, движущийся со скоростью в Магнитном поле индукции В, действует сила qjiTBl*. Если проводник при своем Еер(гме1аен1ш движется так. что имеет составляющ скорости, перпендикулярную силовым ливням магвнтного поля, то иа зарадл. входящие в состав атомов и молекул этого проводника, действуют силы, направленные вдоль этого проводнике. На отрнцагельные эарчаы силы действуки-в одну сторону, иа положительные-в противоположную. Вследствне бапышД способности к пере-усщевин) свободных электронен в проводнике на одном конце его образуется избыток, на другом-недостаток этектроноа (т. е. избыток положительных зарядов).

Явление разделения зарядов в проводнике, движущемся в магнитном поле, представляет собой возникновение в нем индуктированной э. д. с.

Пример 17. Вывести формулу для определения э. д. с. в сймотке с числом вигков ю, намотяннои на прямоугольной рамке площадью 5. Рамкэ вращается сг л окон скоростью © в однородном магнятиом поле с индукцией В=Вф-о

S Jj-bsiTSr ~

Решение. Погокоодепленне обмотки

=шФ= wBS cos ct KpfieS* cos (Of, где a = b>f-yrwi, обраэсваняый плоскостыо ранкн н горизонтальной плоскостью; *~t~ *~ we-<rf dn 0)0=BeSiM- (в cos (uf+® Bin (OQ.

Подсчитаем числовое значение e при

*=1.4-10-.K fe-C.6.3)40,761 В.

thbL? MOHHBjraiHH н 8, д. с. самоиндукции. Ицдук- ивность. Явление наведения э. д. с. в каком-либо контуре при ении тока, протекающего по этому контуру, называют само-

* Заесь €нла Лсренца гтределена при отсутствии электрического поля * >Ю Е. В электрсяяагввтном поле с нап]

Пола Е в

Навнную (кцауктирюаииую) э. д. с назьшаюг э. д. с. самоиндукции и обозначают Ci. Для ее определения необходимо продифференцировать потскосцепление контура ф, вызванное собственным током i.

Из опьп-а известно, что для контурда (катушек) с неферромаг-ниткым сердечником или для катушек с сердечником из магнито-ди5 лек-триков, у которых р, почти постоянна и не зависит от напряженности магнитного поля, потскосцепление $ пропорционально току :

(2.6)

Коэффициент пропорциональности Е между и t называют иидуктивноапью. УЬщуктшасп, как элалент схемы замещения реальной цепи дает возможность учитывать при расчете явление самоин-дукцнн и явление накопления энергии в магнитном поле катушки.

Индуктивность L зависит от геометрических размеров контура (катушки) и от числа витков w, но ие зависит от величины тока, прогекаюшш) по катушке, если сердечник катушки неферромагаит-ный или ферромагнитный, но его магнитная проницаемость постоянна. Индуктивность измеряется в В с/А = Ом с = генри (Г). Таким образом,

(2.7)

Следовательно, э, д. с. самоиндукции в катушке пропорциональна скорости изменения тока в этой катушке. Она равна нулю, если ток не изменяется.

Положительное направление э. д. с. совпадает и с полаж1Ггельиым направлением тока.

Знак минус в формуле (2.7) свндетельсгвуег о том, что мгновенное значение э. д. с. отрицательно прн >0.

Для катушек с ферромагнитным сердечником погокосцепление является нелинейной функцией тока {i) и . д. с. саммшдукции по правилам дифференцирования сложной функции

(2.8)

Производную rii]3/di называют дш,

альной иш

и обозначают L ; t является функцией тока i.

Значение d определяется произведением dl/dt-d/di, где и соответствуют взятому моменту времени t.

Пример 18, Сределить индуктивность кат}Шки, равномерно намотанной на сердечш1К прямоугольного сечения (рис. 2.3), внутренний радиус которого = 4 см, наружный = 6 см, высота й = 2 см; число витков ву=О00; ц = 80 (сердечник из магнитодиэлектрика).

Решение. Напряженность поля в сердечникеопределим по закону полного тока:

Поток через полоску hdR, заштрихованную на рис. 2.3. Полный поток

Погокосцепление = и)Ф.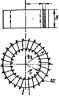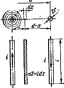

Рнс. 2.3 Индуктивность

Ряс. 2.4

Следовательно,

, 100(P. 1.256-10- -80-2-lO-s , 6

=-- 4-

Пример 19. По катуиже примера 18 течет ток i = /m sin чЛ. Определить э. д. с. самоиндукции в катушке при = 0,1 А и ш = 10 гЧ Решение.

= 0.131 г.

ei= -10-0.131-0,1 costof=-13,1 cos erf В. Пример 20. Опреаелгаъ индуктивность двухпроводной линии передачи длиной i = 10 км при расстоянии между проводами d = 2 м. Диаметр проводов 12 мм.

Решение. Двухпроводаая линия (рис. 2.4) представляет собой как бы один большой виток с током i-=/. Напряженность поля в пространстве между проводами в произвольной точке на линия, соединяющей оси проводов, создается обоими проводами и равна сумме напряженностей. каждая из которых находится по закону \ полного тока (см. § 14.7):

где й - тхг. Поток через элементаркую площадку dS==ldx

dOBdS = Bidx(y-i-)dx. Полный поток*

Если rf>r, то

(2. ГО)

Полртавим числовые значения: L

1.256. йч.! - . 200

1 = 0.0232 Г.

§ 2.3. Явление сап

дукции. Взаим-

ная иидуктнвность.~вление наведения э. д. с. в каком-либо контуре при изменении тока в другом контуре называют взаимоиндукцией.

Наведенную (индуктированную) 9. д. с. называют з. д. с. еэаамо-индукции и обозначают € - Пусть, например, есть два контура, уда-лен[1ых на некоторое расстояние друг от друга (рис. 2.5). По первому контуру протекает ток i, по второму -ток ij.

Поток Ф, создаваемый током i,. частично замыкается, минуя второй контур (Фц), частично проходит через него (Фц) * :

Рис. 2.5 Ф1=Фи+Фи. (2.11)

В свою очередь поток Фа, создаваемый томэм ij, частично замы--кается, минуя первый контур (Фг), частично проходит через него (Ф:

Ф2=Фи+Фа.. (2.12)

Полное потокосцеплсиие первого контура (число витков его i

.... = (Ф, ± Ф,) = ± ф. (2.13)

Полное потокосцшление второго контура (число витков его

по. - - Щ (Ф2± Ф.) = 4г ± (2.14)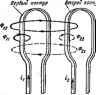

Потокосцеплением в проводах при решении задачи пренебрегаем. Считаем длину / достаточно большой по сравнению с d, что дает основание не учитывать потек пстеречных сторон петли.

Чтобы рис. 2.5 был более понятным, ка нем изображено только по сщной

Если ПОТОК взаимоиндукции направлен согласно с потоком самоиндукции, создаваемым током данного контура, & выражениях (2.13) и (2.14) ставят знак плюс; при несогласном (встришш) направлении-знак минус.

Из опыта известно, что если сердечники катушек выполнал! из неферромагнитных материалов или из фромагннтных, но имеющих постоянную л, то пропорционально i, а пропсрционально i.

Коэффициенты пропорциональности обозначают буквой М с соответствующими индексами. Так,

2i = M4. (2.16)

численно равны друг другу (доказа-

Коэффициенты Mi и Л!, тельстБО см. в § 2.6):

(2.17)

Коэффициент М называют взаимной индуктиеностш контуров (катушек). Он имеет ту же размерность, что и индуктивность L. Полная э. д. е., индуктнрушая в первш контуре.

<2.18)

во втором контуре

Э, д. с. взаимоиндукции

(2.19)

(2.2(9

(2.21)

, В выражениях (2.20) и (2.21) знак минус соответствует согласному направлению потоков самоиндукции и взаимоиндукции, а знак плюс-встречному. При тшш обозначении взаимная индуктивность М всегда поло £нтельна.

Как элемент схемы замещения реальной цепи М позволяет при расчете учесть явление взаимоиндукции н явление йакопления энергии в магнитном поле магнитносвязанных катушек.

В литературе встречается и другой способ записи э, д. с. взаимоивдукцяи;

Считают, что коэффициент М может быть либо положительным (при согласном Квстреч ноим° самоиндукции и взаимошщукцин), либо отрицательным