g 1715. И сационных КС

ння, гри определенных условиях возникающие в нелинейных электрических цепях

Ремтсац

с одним накопителем энергии, например в цепи с одной емкостью (без индуктивности) нлн Б цепн с одной индуктивностью (без емкости)

На рис. 17.3, а изображена принципигльнан схема генератора релаксэцвонных колебаний. Она состоит из источника постоянной э. д. с. £, линейного сопротивления R, емкости С и параллельно соединенного с ней нелинейного сопротивления ЙС, имеющего в. а. к. S-образной формы.

В качестве НС с такой в а. х. могут быть взяты неоновая лампа или тиратрон. На рис. 173, б дана схема генератора г -----

гт собой i

неоновой ламны, прямая 2-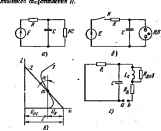

Еслн бы не Сыло релаксационных колебаний, то режим работы определился бы точкой т неоесечения кривой / и прямой 2.

Для атой точки сумма падений рым законом Кярхгофа равна э. д. i

в ооотсетствии с

.... Г с Т

Точку т будем называть точкой равновесия. Она определяет режим работы схемы при прохождении но сопротивлению Ц и неоновой лампе постоянного тока.

Убедимся в том, что режим работы, определяемый точкой т, является неустойчивым режимом: достаточно ничтожно малого отклонения от состоянн сия, чтобы изображающая точка ушлав из точки /и и не возвратит

равновесии, составим

В схеме начнутся релаксацио1Ь1ые колебания.

Для того 4TOfe, убеиатася в нстойч линейную схему аамещения редакеационно!

Так как НС имеет S-обраэную в. а. х., то в схеме для исследования устойч чнвостн оно имитировано (в соответствии с § 175) дифференкнальным сопротивлением Дд и посаедовательно с ним включенной малой паразитной индуктивностью tn, эашунтирозаниой активным сопротивлением Ддоб-

Днфференцнальиое сопротивление Дд в точке т пропорционально Tairrency угла а на рис. 17.3, в и является отрицательной величиной.

Источник э. д. с. в схеме замещения рис. 17.3, а не включен, так как исследуется поведение схемы в режиме приращений до отиошевик к режиму, шред ляемоку точкой i.

1Н0Й фор е относительно точек в и ft

pL Cfi ( доб+й+Р \и (й+йдоб+ +С№довКЛ- доб (ft+ftj=0.

Так как рабочая точка находится /?>Дд о поэтому свободный член пол ю-ч-оэ следует, что Ддоб>?д1. поэтому Состояние равновесия будет неусгойчиыл отрицательным, е. при

в- а. х- НС, то Из условия ReZ(/w)>0 при .leKT прир тоже положителен, коэффициент лрН р окажется

f.fl(R+ftflo6+ s)+Cffft oeJ?fl<0

ны состояний прн релаксационных коле-

Рассмотрим баниях.

Пусть в схеме рис. 17.3, б при нулевых ключ К. Емкость С начнет зарйжаться, и напря (рис. 17.4, с). Так как емкость и неоновая лампа ИЛ включены параллельно, то в любом режиме работы напряжения из них одинаковы. Как только напряжение на емкости возрастет до величины, равной напряжению зажигания неошвой лампы, последний зажжется и ток в ней возрастет от нуля до ij (рнс, 17.4,6).

Емкость быстро разрядится через ИЛ, внутреннее сопротивление которой мало по сравнению с R. Прн S

в точку /.

на в. а, X. ИЛ переместнтся из

В точке i напряжение на НЛ ,

гашения ее щ, п( тому неонован ламйа-гаснет и ток в ней становится равным нулю (точка 2).

Далее емкость вновь заряжается до иапряже-вия Нз, ЯЛ снова зажигается и процесс повторяется.

Траектории движения нзобряжающей точки на рис. 17.4, б образует замкнутую петлю 12341.

Следует подчкнуть, что если условия возбуждения колебаний в схеме млюлневы, то размах колебаний напряжения на i определиется только палряжениями зажигай!

колебаний равен сумме времени зарядки и врек , . . . .

э. д. с. Е, емкости С, сопротивления ft и внутреннего сопротивления НЛ. Обратная связь в схеме находит свое ныряжение в том, что емкость управляет режимом работы ИЛ.

нагрузки ft и э. д. с. Е н

----шия щ НЛ. Период

I емкости и зависит от

вости сяиусоидалымх колебаний ,

целью воспользуемся формулами (16.24) и(16.29).

НС (16.29) производная от амплитуды

А (fl)=da/d(=0,5aftt(l-0,25а ).

юти nq cumeaioro движения в ламповой гене-

Рассмотрим вопрос об иссладованин устойчи- екераторе (см. рис. 15.40). С этой

Ов=2,

В соответствии i жения 11й]св( в .

я режиме работы амплитуду колебаний обозначим Для вняе dajdt вулю и решим уравнение 1-0,25оЗ=0. Отсюда

§ 17.4 для 1

пери<№1ческа> сила частотой га, достаточно вайти янак проазводвоб dA (а) 16*

а=Оа. Если при этом dA (о)Мв<0, то гроиесе устойчив. В нашем случае

Ранее см. уравнение (16.32)J было выяснено, что aM>-RC н *(>0, тан как только в этом случае амплитуда колебаний представляет собой вещественную, величину.

Следовательно, tdAffi)/da) <0. Процесс устойчив.

I. Дайте определение системы, устойчивой в малом, устойчивой в большом, устойчивой но Ляпунову. 2. Изложите общие основы исследования устойчивости в малом. 3. Как но кой>фициет*м характернствческого уравнения, составленного для малых приращений, можно судить об устойчивости системы? 4. В каких группах электрических цепей можно ожидать неустойчнин режимов работы?

б. №образите схемы замещения НС с в. а. -х. S- в N-типа для исследовании устойчивости, когдв изображающая точка оказывается на падающем участке

в. а. X. этих сопротивлений. Покажите, что лля этих схем выполняются условия r6z (/и) <0 и ReZ (/м) >0. 6. Изложите идею исследования устойчивости

вынужденных колебаний и автоколебаиий.

глава восемнадцатая

ЭЛКТРИСНИЕ ЦЕПИ С ПЕРЕМЕННЫМИ ВО ВРЕМЕНИ ПАРАМЕТРАМ!

§ 18.1. Элементы целей. Электрические цепи с пер&х

времени параметрами представляют собой электрические цепи, в состав Которых входят активные сопротивления, индуктивности, емкости и взаимные индуктивности, изменяющиеся во времени (если в состав цепи входят хотя бы в1 одно изменяющееся во време-

-illi- -Vs еопротивлшие, то она при-надлежит к рассмагрнваемому - классу цепей). > г) Угольный микрофон -про-

Рис. 18.1 стейшее изменяющееся актив-

ное сопротивлаше (рнс. 18.1,с). Сопротивление его является функцией звукового давления, оказываемого маабраюй на порошок графита.

Индуктивная катушка с незамкнутым ферромагнитным сердечником, который выдвигается нз катушки н вдвигается в нее (рис. 18.1,6),-< пример переменной во времени индуктивности.

Конденсатор, пластины которого раздвигаются и ошнгаются, не соприкасаясь (рис. I8.I,в), -пример емкости, изменяющейся во времени.

Две индуктивные катушки Lj и Lj (рис. 18.1,е), взаимное расположение которых меняется во времени (например, если одна из них

вращается вокруг своей оси, перпендикулярной рисунку), -пример взаимной индуктивности, меняющейся во времени. -

Изменение параметров цепи во времени- можег происходить под дйствием внешней механической силы или чисто электрическим путал.

Параметр цепи может изменяться во времени периодичежи и вепернодически. Рис. 18.2, а -в иллюстрирует несколько различных пернодическ11х законов изменения параметров.

§ 18.2. Некоторые общие свойства электрических цепей. Несмотря на то что цепи с перемшными во времени параметрами являются линейными цепями (описываются линейными дифференциальными уравнениями), они обладают свойствами, сближающими их с fiJ нелинейными цепями.

Переменные во времени сопротивления, подобно нелинейным сопротивлениям, являются генерорами высших гармоник тока и напряжения, В силу этого в цепях с першеяными параметрами протекают токи не только тех частот, которые имеют источник вынуждающей силы и nqitwaman составляющая сопротнвления, ио и токи множества других частот.

Благодаря этому в цепях с першишыми параметрами при наличии в их составе индуктивностей и емкостей могут возникать резонансные явления на высших и низших гармониках при отсутствии гармоник данной кратности у источника э. д. с.

Обратим внимание на то, что амплитуды отдельных гармоник тока в цепях с переменными параметрами линейно зависят от амплитуд остальных гармоник (в нелинейных цепях аналогичная зависимость нелинейна).

Наряду с этим цепи с горакмными во мени параметрами обладают i

Рис. 18.2

МИ, принципиально отличающими их от нелинейных цепей. Так, в цепях с переменными во времени параметрами амплитуды гармоник тока и напряжения пропорциональны амплитуде вынуждающей силы. Другими словами, еслн э. д. с. кточштка увеличить вдвое, то и амплитуды токов и напряжений увеличатся вдвое. В цепях с нелинейными сопротивлениями, где имеет место насыщение, такой пропорциональности, как известно, нет.

Ранее говорилось, что перемшное сопротивлаше является генератором высших гармоник тока. Убедился в этом на простейшем примере. На рис. 18.3 изображена схема, состоящая из источника постоянной э. д. с. i- и актинного сопротивления, изменяющегося во времени в соответствии с кривой рнс. 18.2, б;

(18.1)

По закону Ома, ток в цепи

Известно, что функция 1/(1-jc) при jcj<l может быть разло- жена в степенной рвд

\/(\-х)=1+х+х+х+ ... -\-х\ (18.2)

Роль, которую играет х в (18.2). в (18.1а) выполняет/с sin cot. Поэтому при *<1

-=l--ftsin6)(+ftsin >(+ftsin (-b ... (18.3)

Воспользуемся известными из тригонометрии формулами S jn*a= 0,5 (1 - cos 2а); sina = - 0,25 sin За -Ь 0,75 sin а; sin* а. = 0,375 - 0,5 cos 2а+0,125 cos 4а

и объединим слагаемые правой части ряда (18.3) с аргументами одинаковой кратности. Получим

-=(1--0,5АЧ0,37БАН ...)--(ft--0.25a4 ...)sino)f-

-(0.5а-Ь0,5ан ...)cos2<o(-(0,25* -- ...)sin3b)f-- ...

Таким образом, несмотря иа то, что в цепи рис, 18.3 включена постоянная э. д. с, а переменная составляющая сопротивления изменяется по закону синуса с частотой ш, ток имеет н высшие гармоники (частоты 2сй, Зю). Постоянная составляющая и амплитуды гармоник тока нелинейно зависят от коэффициента ft, но линейно зависят от э. д. с. Е.

Обратим внимание тзкже на то, что при ftijto постоянная составляющая тока в цепи рис. 18,3 не равна E/R, т. е. в схеме наблюдается своеобразный выпрямительный эффект.

Энергия, выделяющаяся в виде тешюты в цепи с персышными во времени параметрами, доставляется не только источниками э. д. с. (тока), имоошпмиси в цепи, но и теми вншшими источниками (например, механическими двигателями), которые совершают работу при изменении параметра (параметров) цепи.

Какую долю энергии доставляет источник э, д. е., а- акую дает внешний источник, совершающий работу при изменшии параметра, для каждой цепи с переменными параметрами следует рассматривать применительно к конкретным услОБИям. Доля энергии, доставляемая внешним источнике !, может составлять в одном предельном случае нуль, в другом-100%.

§ 18,3, Методика расчета электрических цепей в установившемся режиме. Если ибршенный параметр измениется во времени периодически, претерпевая резкие скачкообразные изменения (см. рис. 18.2, а), то расчет цепей целесообразно проводить с помощью класаиежого метода расчета переходных процессов. В этом случае постоянные ин-

тегрирования определяют, исходя из законов кшмутацни н периодичности процесса.

Если же першашый параметр изменяется так, что его можно представить в виде постоянной составляющей и одЯой или нескольких синусоидальных составляющих, то расчет производят, пргменяя метод гармонического баланса.

Метод гармонического баланса применительно к нелинейным цепям был рассмотрен в § 15.49. Основные черты его и здесь те же. После* довательность расчета такая: искомый ток (или любая другая величина) изоажается в вцде рада Фурье, например в виде

t = /д sin юГ -I- /и cos lof -1- /и bin 2{о/ 4-1 cos 2©/+ ...

Полученное выражение для тока попставляют в дифференциальное уравнение цепи и выделяют из него уравнение, выражающее собой равенство постоянных составляющих левой и правой его частей, уравнение, выражающее собой равенство синусных составлякщих левой и правой частей, и т. д. Каждое из sthx уравнений в общем случае содержит несколько неизвестных (/д, /, /ei. 22). но является линейным уравнением относительно этих неизвестных (в этом отличие от нелиншных цепей). Далее решают систему линейных уравнений относительно /j,

А,. / . /и. / .

лод гармонического баланса можно применять к расчету цепей, содержащих несколько перйленныА во времени параметров (например, изменяющееся во времени активное сопротивление и изменяющуюся во времени индуктивность), причем харак-тер изменения во времени э- Д- с. (тсжа) может быть по любому периодическому закону.

Гример 167. В схеме рис, 18 4. я э. д. с. £ и индуктивность L гостоянны, а сооротнвлеиие меняется в соответствии с рис. 18.4, б. Определить аакон изменения тока в установившемся режиме.

Решение. Твк как сопратнвление изменяется периодически, то и ток изменяется периодиче-,е тока в моме t О че] возрастает от до ft, ток принимает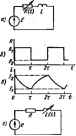

момент сопро-ачнкает умеиь-/1 в сопротивление скачком

уменьшается с Ri до Последнее приводит к тому, что тох начинает увеличиваться.

В первом интервале времени от /=0 до 1=т ток можда предстивип, в ввде суммы принужденного ElR и свободного Се токов, причем pi=-iVt-ко рень характеристического уравнения цепи pL--fii=0; Ci-постоянная нкгегрн

Во втором интертале времени от /=т до t=2z

Задача сводится к определеиию Двух постоянных Ci в Q-