Прм неустойчивом режиме работы в малом достаточно малое отклонение с течением времени увеличивается и система ие возвращается в исходное состояние.

Устойчивым vs бояшиш называют такой режим работы, при кото-рш система, пол>чив достаточно большое начальное сгтклоненне, возвращается в исходное состояние тюсле прекращения действия возмущения.

Если при достаточно большом отклонении от исходного состояния по прекращения деГмпвия возмущения система не возвращается в исходное состоиияе, то ее называют системой, неустойчивой в большом .

Разлитпе между устойчивостью в малом и устойчивостью в большом можно проиллюстрировать с помощью рис. 17.1, с. На этом рисунке изображен жетаб с помешенным в нем uiapiniOM. Если шарик толкнуть так, что он переместится из положения 1 в положение 2, а затем предоставить его себе самачу, то под действием силы тяжести ш1ик возвращается в псхошюе положение (положение равновесия). Если норик толкнул, с большей силой, то ои пройдет через положение 3 и выскочит нз желоба. Таким образом, система рис. 17.1, а устойчива в мал( ( и ~ неустойчива в большом .

В литер.атуре можно встретить также термин устойчивость по Ляпунову . Системой, устойчивой по Ляпунову, называют акггалу, для которой можно указать область допустимых отклонений [область 6(e) на рис. 17.1, б] от состояния равновесия (точки 0), для которой ИИ одно .из движений, начинающихся внутри области 6. никогда ие Д0СТИ1ПСТ граиии некоторо!] звданной области г. Величина области б зависит oi величины области г. В нелинейных электрических цепях в общем случае возможны еле- < дующие режимы (типы движения): 1) состояние равновесия; 2) периодическое движение при отсутствии в системе источников периодической 9. д. с. (тока) - автоколеия; 3) периодическое движение с частотой ис11Ч1П1ка периодической э. д. с. (тока) -вынужденные колебания; 4) резонансные явлсешя на высших, низших и дробных гармониках: 5) кваз1териодические (как бы периодические) процессы по типу автомолуляцин, а также ряд других, более сложных типов движений. Каждый нз этих режимов (типов движений) может быть исследован на устойчивость.

В большинстве практических задач производят исследоеаюге устойчивости в малом . Исследование устсйчнвостн <ш большом пршзво-дят путем анализа хода интегральных кривых на фазовсй плоскости или путем использования второго метода Ляпунова . Основы теории . устойчивости были разработаны крупнейшим русским матеметиком А. М. Ляпуновым в 1892 г. и изложены в его книге Общая задача об устойчивости данження .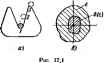

§ 17.2. Общие 0С1ЮВЫ исследования устойчивости в малом*. Общие основы исследования устоЛчивости в малом применимы ко всем

или почти ко всем [Иестным в настоящее время типам движения. В каждом конкретном случае возможны некоторые особенности прн применения общих пр(ЩЦ1(нов.

Для исследования устойчивости исследуемой величине х (величи-нам) дают малое приращение Ддг, развертывают уравнение, описывающее процесс, в ряд по степеням малого при[шщення Ддг и ввиду малости tix отбрасывают все члены ряда, содерж.ашие Дх в степенях выш первой.

В полученном уравнении (уравнениях) выделяют слагаемые, содержащие Дд: и производные от Ajf по времени, и образуют нз них дифференциальное уравнение (>равнения) относительно Дд:. Уравнение относительно Дл: алгебржзнруют, получакя характеристическое уравнение и определяют его ксни.

Если хотя бы один корень характеристическтео уравнения поло- жителей или паюжительна действительная часть кс ап1а(сно-сопряже ь ных корней, то это свидетельствует о том, что возникшее приращение Д будет ис убывать, а возрастать по времени, т. е. исследуемое движение является неустойчивым.

Если же все действительные корни характерпсгаческого уравнения отрицательнЕЛ, а все кс*тлексио-сопряженпые корни имеют отрицательную деГктвшельную часть, то исследуемое движение является устойчивым.

XiaKTepHcnneatoe уравнение, составленное ствоснтельно прира-шмя Дл, для CHcreMtj второго порядка амеет вид

для системы третьего порядка

о..Р=-ь fljp-b OtP-1-Од = 0.

Для сунщения о характере корней характеристического уравнения разработано несколько математических критериев. Воспользушся критерием Гурийца (Рауса Гурвица).

1итериП (теорема) Гурвица состоит в сле,аующе4: для того чтобы действшельные части корней характеристического уравнения былн отрпцательными. необходимо и достаточно, чтобы все диагональные миноры (А Д.. Д -1) определителя Гурвица (Д были больше нуля.

Определитель Гурвица

Щ Ua Оз О Oi Оа

Следовательно, условия отрицатыьности действительных частей кориен характеристического уравнения выражают следующим образом:

>0 и 1

Сам определитель Гурвица Д составляют так:

1) по главной диагонали определителя в гаядке возрастания индексов Бписьюают коэффициенты от о, до 0;

2) в ту часть кансдого столбца, которая расположена выше главной диагонали, вписывают коэффициенты в порядке возрастания индексов;

3 в ту часть каждого столбца, которая расположена ниже главной диагонали, вписывают коэффиш[енть[ в поряяке уменьшения индексов (до включительно).

Следствием теоремы Гурвица является лемма: есе ксьффициепты характеришинеского уравнения (йо, о Rg, .. -, Яп) устойчивой системы положительны.

Из изложенного вытекает, что для сктвш с характеристическим уравнением второго порошка положительные воитствениые корни (или комплексно-сопряженныёс положительной действительной частьк имеют место в том случае, если какой-либо из коэффтшентов уравнении (По, Og, а. окажется отрицательным Для системы с характеристическим уравнением TjieTbero порядка положительные вещестенньЕе корни (комплсксно-сотряженные с положительной дейстыггельной частью) будут в том случае, если: а) какой-либо из коэффициентов [а, о oj окажется отрицательным; б) afi - a< ().

Аналогичные : 1ключенин могут быть сделаны и для систем с характеристическими уравнениями более высоких порядков.

Коэффициенты Оо, о а ... могут оказаться отрицательными в следующих основных случаих:

а) когда в состав исследуемой на устойчивость системы входят нелинейные активные сопротивления, обладающие паданмцнм участком характеристики, и когда точка равновесия оказывается на падающем участке характеристики;

б) в схемах с чрезмерно большим воздействием выходной, величины на входную (б схемах с чрезмерно больпюй положительной обрапюй связью). В этом случае пос17пленне энергии из выходной цепи во входную превышает потребление энерпн! во входной цепи и npnparaeFiHe Ах возрастает;

в) в схемах с управляемыми нелинейными нндуктивностями (или нелинейными емкостями) при наличии неявно (в некоторых случаях и явно) действующих обратных связей. В таких схемах обратные связи прн феделеяных условиях пр1Шодят к появлению на характеристиках нелинейных индуктивностей (нелинейных емкостей падающих участков.

Режим работы систаш может оказаться неустойчивым, если изображающая точка окаж на падающем участие характврисгнки управляемой нелинешадТ индуктивности (управляемой нелинейной (мйобти).

§ 17.3. Исслеорвание устойчивости состоянии равновесия в системах с постоянной вынуждающей силой. Когда рабочая точка по постоянному току окажется на падающем участке в. а. х., то состояние равновесия в актеме при определенных условиях может оказаться неустойчивым.

При исследовании устойчивости нелинейное сопротивление заменяют расчетной схемой -схемой замеще!1ия. Она должна учитывать свойства НС как при медленных (лри w-*0), так и при весьма быстрых (при <11- -со) малых приращениях тока и напряжения ка НС,

Свойсгеа НС при ю -> О определяются самой в. а. х. НС, снят(й прв постоянном токе, на падающем участке которой дифференциальное, сопротивление /? <;о,

Если к НС ггодвести некоторое постоянное напряжение или чеэ него пропустить некоторый постоянный ток такой величины, чтобы рабочая точка находилась па падающем участке в. а. х.. и затем воздействовать на НС синусоидальным напряжением или током малой амплитуды, то сопротивлепие Z(/(u), оказываемое 1]С синусоидалшой составляющей малой амплитуды, дет представля1ъ собой кшплекс-ное число. Опыт показывает, что при достаточно большой со действа тельная часгь этсяо с ч>отивления оказывается патожитсоыюй, т. е. ReZ(/(o)>0. Объяшяется это тем, что физические процессы в самом НС являются процессами инерционными, причем инерционность все сильнее проявляется с росгом -частоты..

В одних НС инерционность вызвана теплсжымн процессами, в других-процессами накопления энергии в электрическом и (нлн) магнитном полях, в-третьих -процессами нонизацин и депоинзации (которые также протекают не мгновенно), в-четвертых - мнерцнониостью процессов диффузии носителей тока и емкостью, обусловленной объемными зарядами. Но чаще всего инерционносп. есть следствие нескольких взаимно связанных друг с другом процессов.

Таким образом, схема замещения НС, когда точка равновесия наход1Ггся на гадающем участке характеристики, но опюшшпю к малым приращениям должна быть такой, чтобы при io- .0 Re2(/ii>) = /;,<C <0, а при иоо ReZ(/O))>0.

На рис. 17.2, а изображена одна из возможных схем замещения для НС с S-образной в. а. х. (рис. 17.2, б), удовлетворяющая перечисленным условиям. В этой схеме -некотсраи малая индуктивность, которую часто называют паразитной , ? об>?к1>О-некоторое добавочное активное сопротивлоше.

На рис, 17.2, е. изображена одна из возможных схем замацения для НС с N-образной в, а. X. (рис. 17.2, е), В пей Сп-некоторая малая емкость, называемая часто впаразитной , и /?дос > О - некоторое добавочное активное сопротивление. Параметры L и R,, а также С и Кдоб зависят от физических процессов в НС и изменяются лри переходе из одной точки на гадающем участке в. а. х. в другую.

§ 17.4. Исследование устойчивости ав1

ных гашебаиий по первой гармонике. В качестве исходных при исбле-

I и ВЫНуЖД(9№;

довании устойчивости автоколебаний и вынужденных колебаний обычно служат уравнения, получаемые по методу медленно меняющихся амплитуд (см. § 16.7). Однако в тех случаях, когда напряжение на каком-либо элшенте (ток в исследуемой цепи) резко отличается по форме от синусоиды, например имеет пикообразную форму, исследование устойчивости целесообразно проводить по средним за полпериода значениям величин.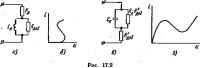

Если через а м Ь обозначить медленно меняющиеся амплитуды синусной н косинусной составляющих 1Кследуемого колебания, то нз исходных уравншнй системы можно волучить два уравнения для медленно меняющихся амилтуд:

daJdl==A(a, Ьу, dbldt = B{a, Ь).

(17.1) (17.2)

Здесь Л и В являются функциями амплитуд а к Ъ, функциями всех параметров схеиы, угловой частоты колебаний и амплитуды вынуждающей силы. Обозначим значения о и Ь в установившаяся режиме, огда амплитуды не изменяются во времени) через щ и Ь. Для определения Оо и fco в (17.1) и (17.2) следует положить dajdt - = 0 н db/dtO и ренцпъ систему уравнений:

(17.31

В(йо. i>o)-0. (ПА)

Пусть в результате возмущения амплитуды колебания получили малые приращения Да и Д6 и стали равными: а = ао+! и b = be + + Дй.

Подставим этн значения а и 6 в (17.1) и (17.2), развернем А(ао + + Да, feo-J-ДЬ) и В(Оо--Да, Ь--АЬ) в ряд Тейлора по малым приращениям Да и Д6 и в силу малости приращений ограничимся слагаемыми рада с первыми степенями Да и ДЬ. Получим:

Л(о -1-Да, Ь + Щ = А(щ, 6о)-ЬДаЛ1--Д&В (17.5)

В(о -}-Да, Ьо + ЩВ(ао, Ь) + AaAs+АЬВ . (17.6)

Для сокращения записи обозначено:

Индекс у свидетельствует о том, что в частные производные должны быть подставлены значения я и 6 установившегося режима, т. е,

., [иенты Л, Ag, Ва являются функциями и 6о. не являются функциями приращений Да и дЬ. Подставим правые части (17.5) и (17.6) в (17.1) и (17.2), учтя при этом (17.3) й (17.4). а также то, ,то Lit J .

В результате получим два уравнения:

daJdt=Л , Да -Ь ВДй; (17.9)

d&b/dt = АЫ -Ь ВвДб. (17.10)

Алгебраизируем их:

pua=iAa--BiA&; (17.9а)

рДЬ = ЛДа-Ь ВвЛЬ- (17.106)

Составим характеристическое уравнение

pHmJ+flO, (17.11)

т=-(Л,-ЬЛ5); (17.12)

9=ЛlBa-BЛ2. (17.13)

В соответствии с критерием Гурвица для затухания прираща1ЯЙ Да и ДЕ> необходимо, чтобы

т>0. </>а (17.14)

В автсколебагелыплх системах периодические вынуждающие силы, как правило, отсутствуют, поэтому обычно можно взять 6=0, тГе. взять колебание в виде a(t)s,\n(i)t (см. пример 165). В этом случае вместо даух уравнений (17. н (17.10) будег одно уравнение

dajdtAAa. (17.15)

(17.16)

Для устойчивости автоколебаний в этом случае необходимо выполнение условия Л-,<0.

Пример на исследование устойчивости автоколебаний по формуле (17.1?) см. в§ 17.6*.

Исследовавне устойчивости вынужденных колебаний на высших гармониках й субгарйоникрх, процессов в цепях с переменными во времени параметрами, атакже нссведование устойчивости процессов автомодуляции даны, например, в21.

1в Зч\Ш 465