Постоянную

туды напряжения и-

я Ci опраделвм по начапьному яначёнию амплн-н при (=0 Uc=Uc (0 ), то

ВШ--з5м -

(16.32)

§ 16.8. Переыагинчиванне феррнговых сердечников импульсами тока. В устройствах вычвслш льноВ техники в лйчестве запоминающих алементов применнют миниатюрные ферритовые сердечники различной формы, в частности кольцевые с внешним диаметром порядка 1 мм из материала с примоугольноВ петлей гистерезиса Через отверстия в инх пропускают проводники, являющиеся одно-витковыми обмотками (на рис. 16.8, а показан только один проводник). При

Рис. 16.8

записи

--..in .. у.ч о одному 1 --- . ..j.i...yi:KaRir примиvigjibHUH ИЛИ

почти прямоугольный импульс тока (рнс. 16.8, б) длительностью всего в несколько десяпсов наносекунд или несколько микросжунд. Под действием этого импульса сердечник перемагничиваегся. Хотя в ферритовом сердечнике и отсутствуют макроскопические вихревые токи (в нем нст замкнутых токопроводящнх ионтупов нграющях роль вторичных обмоток трансформатора), перемагинчнвается оп все же ие Мгновенпо.

На длительность процесса перемагничивания сердечника прн выссжнх скоростях перемагничивания решающее влияние оказывает магнитцдя пязкость. Она f!! ! внутреннее поле трении, которое влияет на проне? ; перемдгнччи-ваний. Эт* влияние зависит от величины и скорости изменения намагенченивсти cHifi. У * напряженности поЛ i/ ад и ит При MareMaTV4ecKOM описаинв тормозящего действия магнитной

пропускают прямоугольный i

исходят иа урав1

И.-Н..-о.

(16.33)

где Wo-

ТжпТ Р KiJropoM происходит перемагннчиввнне фер.

ПГ: Я tVomo больше ,<,u oil силы Н, го eiarjnecKoii nSe гнетерезнса; Но находят опытным путем для каждого типа феррита.

Напряженность анешиего поля, вызаанивя током i. H ii ;i, где ш-чИсло

витков, /-длина ср 454

нтной

Члев о-учитывает тормозящее действие магнитной вязкости. Множитель

, где ft-некоторый коаффнцнент; J-текущее

ченности; Jg-намагниченность насыщения.

Решим уравнение (16.33) относительпо dJ/dl, заменив J на индукцию В а /я на индукцию насыщения Bj. Получим уравнение огносительпо В:

(16.34)

If=.(,--), .,.

Это уравиенив с разделяющимися переменными. Яэ (16Л4) следует, что для перехода ив точки 1 в точку 4 (рис. 16.8, в) под действием импульса тока i длительностью * должно выполняться соотношение

Еслн we 5 (Нин-We)d(<JW, то изображающая точка из положения / после

прекращенвя действия импульса перейдет в точКу 2 или 5 или ни подобную

(конечное состбяине зависит от величины (Инн-н амплитуды нипульсй

тока]. Из состояния / и состояние 4 сердечник может быть переведен и иным путем-путем воздействия на него несколысинн следующими друг за другом

U одинаковой полярности, длЯ каждого из которых

(Ннн-И

После нервого импульса рабочая т жение S, после второго нз 2-в S

§ 16.9. Определение фазовой плоскостн и х)акте1>исп1кн областей ее применения. Качественное исследование процессов в нелинейных злектрическвд цепях, шисываемых дифференциальными уравненнинн первого и особенно второго порйд-кои. в ряде случаев лрмгаводят с помощью фазовой плоскостн.

Фазовой плоскостью (ф. п.) называют плоскость, по оси абсцисс которой откладывают исследуемую величину (назовем ее х), а по оси ординат-пронвводную от нсслсдустюй величины dxIdt (последнюю принято обозначать .

В литературе можич встретит, и другие виды фазовых плоскостей: 1) когда , по оси абсцисс откладыопется какая-либо одна величина (например, ток первой ветви), а по оси ординат-другая величии (наг

..J второй ветви); 2) . соЛавлнющей колебания, в по осы 1фдннет-ai колебания и т. д.

В какдой конкретной задаче под либо заряд, либо индукцию. Любому ( соответству ----------- -

(Туда косинусной составляют либо 1

к, либо напряжение, и у исследуемой цепи

Для качественного йсследоваиня процёссм в электрических цепях, описываемых уравнениями третьего порядка, применяют трехмерное феэовое пространство. На одной оси декартовой системы этого пространства откладывают аначение функция х,- на другой-di/dt, на третьей-dr/di

Качественно исследование-это выинление общих снойств исследуекюй цепи без интегрирования нелинейного дифференциального уравнения. Под общими свойсгБЯМН понимают обычно зависимость характера нережщиого процесса от началь-

леме авттаго1ибаи11Й. реэонвнснь , перечисленных режимов и режи-

Все эти вопросы в ряде случаен можно решить н цным путем, без npHajjCTe-Я ф. п. Применение пияедвев делае вссле1говйние CoJlfig Наглядным я оправд,-

нов равновесия-

I меньше объема работы пря

в тех cflyfaBx, когда объем работы сонзмерви решении тех же задач иными методами.

Обычно ф. п. применяют для исследования продесссв в электрических вдпях, содержащих источники постоянной э. д. с. и не содержащих источннкн периодической э. д. с. Однако ее можно нспольвовать и для исследования процессов в цепях, содержащих нсточнихн синуссащальиоВ (постоянно э. д. с, если предварительно перейти от уравнений, составленных для мгновенных значений, к уравнениям для медленно меняю1№хся составляющих (веничин).

6.10.

1Т ральные кривые, фазовая траектория я предельный цикл. Зависимость y=f{K), получаемая нз решения дифференциального ураннення сисггемы, представляет собой семейство кривых на фазовой плоскости, соответствующих различным значениям постоянных ннтегрвропання. 1нвые у=Цк), соответстазто-шие различным начальным условиям, называют штенраамши кривыми.

Начальное положеяис изображающей точки на ф. п. определяете) и dxfdty при /=0.

Интегральную кревую, проходящую через точку ф. п. с заданными ными условиями, называют фазовой траекпюрией.

Вид фезовой траектории вавнсит ог кшфигурацни схемы, характера нелиней-

. Если э

о через ннтераалы времени, равные периоду процесса, соответствующие друг другу значения X и dxldt=-y повторяются й фазовая траектория в этом случае является замкнутой кривой. Замкнутую фезовую траекторию называвэт предельным

Если интегральные кривые и .снаружи н изнутри навиваются ва предельный цикл, то его называют устойчивым, если уда-процесс непериодический, то фезовая

траектория представляет собой незамкнутую kphejto.

. Фазовую траекторию можно наблюдать на экране электроннолучевого осциллографа. С этой целыо на одну нару отклоняющих пластин его подангт исследуемую величину X, а за другую пару-производную от х.

§ 16.11. I

е цростеВшия иромессоа ка фазовой плосмктя. Расе*

рим несколько простейших примеров на описание процессов в линейных цепях.

Требуется изобразить на фазовой плоскости нереждный процесс в схзме рис. 16.9, п. вызываемый пра нулевых начальных условиях замыканием ключа. Обозначим i-ток в цени, и-к:тяжгят иэ емкости. В уравнение цепи Д( + duj-

-и=Е вместо i иодставим С-:

Положмм U(=x, dU(.Jdl=dx/dl=y, тогда у=(Е-х)/ЙС.

Последие* уравнение описывает прямую аЬ рнс. 16.9. б. котт>рая является фезовой траекторией рассматриваемого процесса. Точка ft-зто точка равновесия.

В качестве второго примера ряссмогрнн в 1Я £,=/mSinttf (рнс.16.10,я). Обозначим i=x, тогда

y=dx/dt=u)lm

Разделив г

/ , второе-на возведя в квадрат полу-

получнн уравнение эллипса:

ченные выражения к

(*/и*+1{/(и/ 1] =1-

Следовательпо, изображением синусоцдального пропесса (фазовой трвекторней) ва ф. п. является эллипс (рис. 16.10,6).

Няправленче даяження изображающей точки показано стрелкой. В еерхией

полуплоскости у=->Г>; следовательно, изображающая точка движется в сторону увеличения координаты к. В нижней полуплоскости (/= -<0, поэтому изображающая точка движется в сторону уменьшения координаты x. В целом перемещение изобраяающеВ точки иа ф. п. происходит всегда по часовой стрелке.

§ 16.12. Изоклины. Особые кнки. Построение фазовых траекторий. Тан) сне угла наклона, образованного касательной к интегральной кривой в неко торой точке ф. п. н осью абошсс, определяет величин; dy/dx в этой точке. Совокупность точек ф. п., для которых dyldx=caDd, называют изжтшой. На ф. п. можно провести множество изоклин, лля каждой вз которых свое значение djfjdx.

Длн всех точек ф. п.. оюСражающей процши в цепн второго порядка (кроме особых точек), dy/dx имеет вполне определенное значение. В особых точкак (о. т.) dyldx=O/0, т. е. не определено. Через эти точки Может быть проведено множество изоклин с различными эвачениями dy/dx.

Особые точки классифицируют по виду ннтег-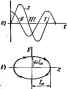

Рж. 16.10

ральных кривых, окружающих эти точки.

Если о. т. окружена эллипсами (рис. 16.11, а), то ее называют о. т. тина а соответствует двум мпимым корням характеристического уравнеиня.

----------------- спиралью, то ее ивзывагот устойчивым

.-сопряженные корни с отрн-

центр; с

Если о. т. окружена сверпыванщейся фокусом (рис. 16-11,6); ей соответствуют цательной действительной частью.

4ь . 4

gj в) г)

Рис. 16.11

Если о. т. окружена раскручиваюшейск спиралью-неустойчивый фокус (рнс. 16.11, в), то ей соответствуют комплекспоч;опряженные корни с положительной действительной частью.

Если корни отрицательные и деВствительвые, то о. т. типа устончнвыП узел (рнс. lail, . При помакктеиьных действительных лориях получают о. т. типа неустойчивый узел (рис. 16.11, в).

Когда одни корень положнтелен, а другой отрицателен, о. т. т (рнс. 16.11.

Пример 166. В цепн услввнях: £=1 В, =1 (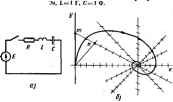

Вывести формулу для построения семейства изоклин для напряжения на 1 Ug. Опредйюгь положение и тип о, т. Построить фазовую траектсню переходного процесса.

Решение. В уравнении цепн

учтем, что t,=R=C=£=l. Решям уравнение j,.+j,+x=l относительпо у и относительно йу1йх:

dx у <0)

Из уравнения (б) следует, что координаты особой тоЧкн =0, х=1. После-довательпо придавая dy/dx значении О, I, 2.....со, -I, -2, .... строим семейство изоклин (рнс. 16.12, б). Все изоклины проходят через о. т. и представляют собой прямые линнн (цепь линейна). Масштабы по осям х и у приняты одннако-выт. Черточки на каждой изоклине характеризуют значение dyldx для нее.

Так как х(Щис10)=0 н (0)=(<luc/difjo=0. то к началу процесса изображающая точка нахопзатся в начале координет.

В установившемся режиме jc=l и уО.

Для nocTpoaiHB интегральной кривой нз исходвой точки х=ви=0 проводам два луча до пересечения I изоклиной rfj№= 1 в точках тип. Первый луч соответствует значен11ю dy/dx=co той изотлины, с которой начинается движение, второй-энвченйю dyldxl следкяцей изоклины, иа которую точка перейдет Лелям расстояние тп пополам и проводим через исходную и полученную точки

плавную кривую-вусочек фазовой траектории. Продолжаем аналогичный процесс далее и строим всю фазовую траекторию в виде свертывающейся спирали.

Qcflfia точка в примере является устойчивым фокусом. Время е явном виде на фазовое нлфскастн не втражец*.

Временные зависимости х=/(0 но фезввой траектории y=dxldt=fp(x) получают по формуле (=J dx/tf(x). где д,-начальное значение х. ж-текущее.

В окрестности точки пересечения крнаОн ф(дг) с осью абсцисс подынтегральное выражение стремтся к бесконечности. Чтобы избежать планимегрнрЬвания площади иод кривой, уходящей в бесконечность при ф(х}- -0, подсчет времени ut -1 этом участке производят по средней скорости фср(ж) на этом участке: Л* =

:р (*)

ведены, например, в \Щ.

я ф. п. пря анализе процессов е

нейных цепях при-

1. Охарактерячуйте известные Вам группы методов расчета переходных процессов в нелинейных цепях. 2. Укажите, в чем пшюжительны! и в чем отрица-гел\,Яые стороны расчетов по мгновенным значснкям н по сгибающим первых гармоник, графо-аналшячеаига и аналитических методов? 3. Почему метод расчета, основанный на графическом подсчете onpe.ie.ieHHoro интеграла, неприменим даж? ддя пеней первого порядка, если вынуждающая сила является функцией времени? 4. Почему метод интегрируемой нелинг.йной яппр9кснмпцни не удается применить к элёктрнчесжнм цепвн, описываемых уравнениями второго и более высоких порядков? Б. Чем физически можпо объяснить, что при подключении линейной цепи RL к источняху сниусондальноВ э. д. с. максимпльное значение тока при переход1Юи процессе це можег превысить >7Щоеннопо значения амплитуды тока установившегося режима, тогда как при подключеяин цепн К- нелинейная индуктивность к источнику синусоцдальной э- д. с. это превьппенне может быть по мндго раз больше? 6. Покажите что метод расчета переходник npoiccoB, основанный на замене определенного интеграла приближенной суммой по 1)врмуле трапеций, применим к уравненнин второго, третьего и более высоких порядков. 7. Охарактеризуйте идею метода ыедлетно нзменшицнхся амплитуд. S. Как расчетным путём учитывают магнитную вязкость при перемагничивании феррнтовых серлечиикэв импульсами тока?

глава семнадцитая

ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ РЕЖИМОВ РАБОТЫНЕЛИНЕЙНЫХ ЦЕПЕЙ

§ 17.1. Устойчивость в малом и в большом . Устойчивость ио Ляпунрзу. Режим раб19ты эласттеской цепи, содержащей нелинейные свпротинлшия, может быть либо устойчивым, либо неустейчи-вым. Как правило, режим работы большинства электрических цепей является устойчивым и в значительно меньшем числе случаев - иеус-

ТСИ1ЧИВЫМ.

Различают устойчивость в малом и устойчивость в большом .

Под устошшвым режимом работы еЗ малом понимают такой, прн котором достаточно малое ошлоншие режима работы от псходаого (установившегося) - независимо от того, какими причинами оно вызвано, с течением времени уменыиается и система возвращается в исходное состояние.