вевных значение можно получить в. а, х. дли первых германии я в. а. х. для действуюшнк вначениЙ величин? 4. Начертите схемы замещения электронаой лампы и траизистора дяя маль переменных составляющих. Б. Охарвкгёрнзуйте основные положения известных Вем методов расчета .периодических процессов нелнвсй-ных цепей. 6- Сформулируйте условия нахождения моментов времени открытии и закрытия днодой. 7, Определите, что понимают под автоколебаниями; как выявить условве, когда онн возникают. 8. В чем причина воаниквовения сгармоническнх колебании? В. В чем принципиальное отличие феррорезонанса напряжений н токов от резоввисов в соотаетствующих линейных цепях? 10. Что понимают под частотными характеристиками нелинейных цепей? II. В чем сходство и в чем различие в построении векторных диаграмм по первым гармоникам для нелинейных и лянейныл попей? 12. Дайте определение понятий индуктивность рассеяния , рамагни1и1!,-лощий токв, сток готерьв. 13. Постройте векторную да аграмму транс-форматоря со стальным сердечником при актив но-илкостаон нагрузке. 14. В чем идея метода малого параметра? 16. Запнпште рекуррентное соотношение, являющееся решением нелинейного интегрального уравнення. 16. К нелинейному актав-иому сопротивлению с симметричной характернстякой приложено перисщичееное напряжение без постоянной составняювден. Можно лн утверждать, что. протекающий через него ток не может содержать постонкную составляющую? 17. Решите вадачи 10.9; 10.10: №.20; 10 ЮЛв; 10.38; 10.39; 10.41; 10.4 10.58; 10.61.

ГГАВА ШЕСТНАДЦАТАЯ

тРЕХОДНЫЕ ПРОЦЕССЫ в НЕЛИНЕЙНЫХ ЭЛЕМРИЧЕСМИХ ЦЕПЯХ

§ 16.1. Общая характеристика методов анализа и расчета переходных процессов. Методы анализа и расчета пд)ехсдных процессов в нелинЫЫых цепях могут быть классифшкжаны: а) по .виду основных операций, которые необходимо выполнять для интегрирования нелинейных дафференциальных ураввений, - на графические рафо-аналитаческне) и аналитичесю! по характеру веяитаны, для которой производится расчет фасчет по мгновенным значениям токови напряжений и расчет по мгновенным значениям огибакяцих токов н напряжени.

Под графичеааши (графо-анатитичеааши) пониманэт такие методы, 9 которых основишт операциями прн определении зэвисгалосш от времени искомых токов и напряжений являются графические построения, нередко сопровождаемые и некоторыми вспомогательными числовыми подсчетами.

В графических (храфо-аналитичесзшх) методах характч)И.Тики нелинейных сопротивлений обычно не требуется выражать аналитически.

В данной гл раеанвтрены слеадшяцие графические методы: 1) метод, основанный на графическом прдеяете определенного интеграла (см § 16,2); 2) метод, основанный на замене определенного интеграла приблшкешой сушюв по фсриуле трапеций (см. § Ш.5).

Аиамитшнеашлш называют такие методы, в тшторых основной операцией при определешш зависимостей искомых токов и напряжений от времени является точное (приближенное) аналитическое интегрирование дифференциальных уравнении цепи путем использования аналитических выражений характ)истик нелинейных сопротивлений.

PaccMDTjjeinj следующие аналитические методы: 1) метод интегрируемой нелинейной алтфоксимации g 16.3); 2) метод кусочно-линей-

ной аппроксимации 16,4); 3) метод медленно меняющихся амплитуд (§ 16.7).

К группе вналшнчЕских относятся также методы, рассмотренные в § 15.69 и15.70. Графические методы имеют следующие преимущества перед аналттркскйми: а) отсутствие необходимости выражать характеристики нелинейных элементов аналитически, что позволяет избавиться от погрешностей, связанных с аналитическим представлением характеристик; б) простота учета гистерезиса и других сложных нечинейных зависимостей.

В свою очередь аналитические методы также имеют перед графическими преимущества. Из них основным является то, что они дают возможность получить paueiuie в общем виде, а не для какого-то одного конкретного сочетания параметров. Получить решение в общем виде желательно потому, что анализ его позволяет выяснить все особенности процесса при изменении всех параметров.

Как уже упоминалось, все методы расчета могут быть подразделены на две подгруппы: Hqрасчет по мгновенным значениям токов и напряжении и на расчет по мгновенным значениям огибающих тоКов и иаприжений.

Расчет по огибающим важен, потому что он дает возможность, ие вдаваясь в мелкие детали процесса внутри каждого периода дей-ствукщеи в схеме периодическсда э.д.с. (внутри каиадого периода автоколебаний в автоколебаткльной актаяе), судить о макроструктуре процесса. Расчет по оп1баю1Еим возможен не только для нел1шейных цепей; он представляет существенный интерес н для линейны.ч цепей.

Точность расчета по огибающим уступает точности расчета по мгновенным значениям. Однако относительная быстрота протедення расчета по огибающим и возможность судить о макроструктуре npoiftcca часта явлиются рвнакяцнми факторами.

Таи, где это необхсдшмо, целссооизно дополнять расчет по огибак>-пщм рэсяепж по мгновенным значениям. Метод расчета по огибающим лредатавло! методом медленно меняющихся амплитуд (см. § \Л\. Все остальные методы относятся к подгруппе расчета по мгновенным значениям. *

Довольно часто апектрнческие цепи содержат несколько нелинейных сопротивлений. Переходные процессы в таких цепях можно рассчитывать методом Волынкнна (см. § 16.5).

Тесрин переходных процегеов в электрических цепях с управляемыми нелинейными индуктивньинв, емностяыми и активными сопротивлениями выходит эа рамки курса. Интере(ющи например, по

i вопросом могут ознакомиться с i

g 16.2. Метод расчета,

на графическом подсчете

определенного интеграла. Метод расчета, основанный на графическом подсчете определедкого интырала, примшнм к нелшоЬым SLietcrpn-ческим цепям, описываемым дифференциальными уравнениями первого порядка, допускающим разделение переменшос. Последняя оговорка очень существенна. Она свидетельствует о тш, что метод применим к еояи ш(по 1ЯОТО и, кж вравнло, неприменим к цепям перемен-

ного тока. Оаювиые этапы и последмательность расчета проиллюстрируй* на конкретном примере.

Нелииейваи емкость через сопротивление fi пощипотается к источнику напряжения V {рис. 16.1.11). Кулон-вольтная характеристика емкости задана графи-

Рис. 16.1

чески (рнс. 16.1, б). Полагая, что в схеме нулевь кривые иэменеиня заряда q, напряжении ва ei времени.

Составим дифференциальное уравнение: Разделим переменные;

(16.1) (16.1а) (16.2)

Для иостроеинЯ крнаойР(ч) ис. 16.1.в) нспольэусм кулои-вольтную характеристику. С этой ие.тью задаемся произвольным значением q. По йулон-вольтной характеристике находим соответсгеующе ему и по (16.2) подсчитываем F (в). Пря 5=0 н=0 и F(e) = l/t/; при f (в)=со. Левую часть уравнения-

(16.1я) проинтегрируем по / от О до текущего значения t, а правую-по от = 0 до текущего значения q. Получмм

*=fi5f(g)dg.

(16.

Гра(ческн подынтегральное вы] jfOBaHHjTO площадку рнс. 16.1, е.

Согласно уравнению (16.3). дли определения времени t. етвому значению q, нужно подсчитать площадь, выражен

F (ф dg представляет совой заштрн-

ингегралю) jF(fl)dq. н умножить ее на сопротивление fi.

Кривая / рис. 16.2. а качественно представляет собой зависимость д иг t. С помощью кривой q=f{t) и кулои-вольтной характеристики нелинеЙиоВ емкости строят заниснмостьИс=/(О (кривая 2).

Ток в цепи для произвольного момента времени определяется го формуле r=(t/- c)/fi (кривая S).

§ 16.3. Расчет методом интсгри

Метод интегрируемой нелинейной алпроюжмации основан на ашняоз!-444

маций характеристики нелннетнсях сопрогивлатя такой нелинейной функцией, которая, во-первы.к, достаточно точно отображает характеристику нелинейного сопротивлении в Тфедполагаемсм интервале перемещения изображающей точки по ней и, во-вторых (н это главное), дает возможность точно проинтегрировать уравнение в известных функщ1ях. Ценность метода заключается в том, что в результате интегрирования получают зависимость исследуемой величины от вралени и от всех параметров схемы.

Метод применим к диффф£шщальн1.гм уравнениям первого порядка, а также к уравнениям, сводящимся к уравнениям первого nopiyyia путш замены перемятых.

Рнс. 16.2

Пркмер 162. Определять закон нарастаичя ] ключа в схеме рнс. 16.2, 6. Зависимость тока i индуктивности выражена формулой i=k<. В с:

нулевые уравнения цепи -

а i прв ;

: условия.

l+tiiV следует.

Обозначим /у= Получим:

а н заменим на ф!; в

С помощью (16.4) МОЖНО определить t шеине ijl достигло яаданной величины.

§ 16.4. Расчет методом кусоч!

*я, которое необходимо, чтобы ота -

йной аппроксимации. При

расчете методом кусочно-линейной лппрогажмацни осуществлйется замена характеристики нелинейного гснфотивлепия отрезками прямих линий, что позволяет перейти от нелинейного диф4 ро1циального уравнения к нескольким линейным уравнениям, отличающимся друг от друга лишь значениями коэффициентов.

Каядое нз линейных уравнений справедливо длн того интервала вршени, в течение копото рабочая точка п)шеи1зется по соответствующему линеаризован FiOMy участку. Метод примшим к цепям, содержащим источники постонннсш и (или) синусоидальной Э.Д.С., к цепям первого V более илсоких порядков.

- Для СЛОЖНЫХ нелинейных цепей с нсточником (истлииками) синусоидальной Э.Д.С.. основная трудность расчета данным методом заключается в определении постоянных интегрирования, исходя из законов

НИЛ участке. В слож-

шмутации и времени работы на каждо]

ных цепях неизвестные определяют обычно из транщащентных уравнений, часто применяют ЭВМ. Впервые идея этого метода была высказана русским физиком Н, Д. Папалекси в 1912 г.

Рассмотм основные этапы расчета ва иросгеВшем

tipmep 163. Емкость С заряжается через НС от источника постоянного напряжения U (рнс. 165, а). Определить закон мэыеиешш тока в цеш при зарядке

Решение. В.а.х. НС заменим лвумн отрезканп прямых линий (рнс. 16Лв). Пусть на участке от t=0 до i=ii Де Uj,-яапряжение на нелиней-

ном сопротавленин: Аг-коэффицнент. На участке t>

Размерность i

ффнциентов iii wHg равна размерно-i уравнение цепи U£-и=t вме-

j /Л. заменим лля первого

1. а для второго-на ki.

до нули. Поэтому авображаюшая точка пмацается мачала йо первому ¥частку. а затем по второму.

Для первого участка

Для первого участка

Постояинуто интегрирования найдем из начального Поэтому t/o+ftii(0+)=W и H0)=Ai=(JJ-O/k,. Следовательно, прн работе а первом участке

условия: /=0, и=0.

Пуст решим п1

к Яадставяма (16. вместе i в li вместо ( к

евие йиюснтельно in

(16.6)

причем Ai=li,

Практически важной является задача о переходном процессе при подключе-тв менагруженяогоратофврматора (с разомкнутой вторичисД (Лмотаой) или нелн-11ехж>й вщдукпмввот к исижниГ лияуиждвльной э.д.с £rtSm(a>;-f- (рис. 1Ё-4, а). Рассмотрим 9т аалачу качествеищ).

Если аитнкное св14ютп81няш i

. . при ззыыканвн ключа в монюгв 9j(.c. £и sin (w+V) проходит черед нулевое аначеиие, в цепи возв1г большие кратковраиенные Соснк тока. Последние мв ут imSHtuaib . шиит тока холостого кода трансформато1>л в 20-50 раз в дужр более. Физически о возникают вследствие того, что к концу первого полунриода {njio) п иие дветирае! величины, близкой к

Из кривой рис. 16.4. 6 видно, что если- то в цепн будет очень

большой ток, во м1юг0 раз превышающий ток при

Хо¥* (оскв тока и очень кратковрижнвы, по все же в системах с мощшни трансформаторами они нежелательны, так как треб1чот пртятня свецнальных Mes> для увтрмиюм вредных последетвнй;

§ 16.5, Метод расчета, основан!.- жблнижянов суммой. Еще в 1910 г. ]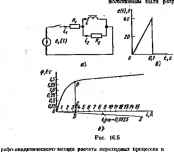

основанного трапеций.

Из курса математики иетестно. что еслн интервал опрщеяениом шкпгт /(х> раэЪгм на а ymu

нелинейных цепях, суммой по формуле