r-a- с

На рис. 15.38, б изображша в, а. х. диода. В целях облегчейия анализа вместо нее будем пользоваться идеали-зиржаннсй в. а, х изображение на рис. 15.38.,

В соответствии с этой идеализированной хактериетжой, через диод проходит ток. паление напряжения на нем ржно нулю и, следовательно, со1фогивлаше са-if мого диода равно нулю. Korj

иапряже! вадиф1е01рицатель-но (т. е. отрицательна взятая 1i направлении стрелки рис. 15.38, а разность потенциала на самск дисйе), диод не щштщ тж и сощсяши1еше его рм-(} \ i, но беаяякчности.

Диод открывается, когда пряжение на нш, личиважь, становится равным вулю, и крывается, кетда ток чфез него, уменьшаясь, стэповится равшл* нулю.

Рассмотрим работу мостовой схемы рис 15.37, а.

Источник э. д. с. включен в одну диагональ этой схемы, а нагрузка, -в другую. Диош работают иопгрно.

В первый полупериод, когда э. д,с. e(t) действует согласно с-положительным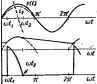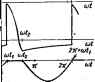

напряжения на диодах 1 w эти диоды протодят ток, а диоды 2 и 4 тока не проводят. Во второй полупернод, котда э. д. с; e(Q изменит знак и действует сог- лаено с тхиснкитеп

лениш напряжения нз диодах 2 и 4, ток проводят диоды 2 и 4, я дшды i и Э тока не проводят. Направлагае тфохождения тока через нагрузку показано карие. Ряс. 15.39 15.37, а стрелкой. Ток чез на-

грузку протекает все время е одном и том же направлении. Форма напряжения на нагрузке иллюстрируется кривей рис. 15.37, б. Через обозначено среднее значение напряжения на нагрузке.

вьа1р 1лишя, когда

. Расшсприм работу с

ваграаКн шунтирована емкостыо С (рис 15.39 а); e(0=£ aactrf.

Решенве. По законам Кирхгофа, +u=e(0, сЛ-= i+a- ветствнв с в. в. х. рнс. 15.38, в днод закрыт и сопротивление его теоретичесяя

бвно-бесюшсчйости, когда i

I. Диан отрыва-

а момент otti, когда нанряжение на i ввтся равным нулю. Как только даод сокроется, напряжение на емкости становится равным 9. д. с: и=Е sin

Как только диод откроется, ток череа емкость станет измениться но закону

ia=C-=mC£, cosei( {пунктир на-рис. 15.39. ф,а ток через нагрузку-позакону =-einoji (пунктир с точкой на рис, 15.39, а). Ток через диод i=ii+i=

i=-=- n©i (пунк! = Lc cos ш(-fsin и

диод закрывается; tgftrfE=- >Cft orfe=arctg(-оОД; ( =/? ).

В интервале от ufj До Zx--cili емкость разряжается на Кд (рис. 45.39, е) и напряжение иа лей изыениетси ио времени по показательному закону =

= £ sin ( , orf>*)( (см. гл. 8).Прв этом (=Ыс/й . (кри-

вые рис. 1S.39, д, е). Заввсиыосп> Ugiat) изображена на рис. 15.39, ж. Момент открытия диода определим из условия ii{w/i)=e (ш]). Из этого условии получаем траисцетщевпюе уравнение относительно со/,: (Вя+пК,- а<,) sinw(2e =sincufi.

В следцтощнЙ вернвд процесс повт1Ч)Я£тся. Чем барн.ше величина ЦС во сравнению с периодом 2iW<u, тем леньше пульсация иаяряжения на дагрум(е Л ,

§ 35,65. Ламповой генератор. Ламповьй генератор * является простшим, иесодержащим подвижных частей преобразователем энергии источника постоянной а. д. с в !Л!ию н)еменвнч) тсжа.

Воаникж1Щие в ламповсм генераторе колебаний онюсятся к классу юмюбаннй. называемых шпжооебашями.

Автокомпания представляют собой периодические колеба1ия, вганикающие в (жетемж, атоднщихся под воздействием постоянных вынуждающих сил (сил, не являющихся функцией времени).

В системе, описанной здесь, источником постоянной вынуждающй силы йвяяегея встоадик постоянной э. д. с. £j.

Рассмотрим тшщип ра&лы лштваго генератора с колебательным жсяггурсм в-деви сетки (рис. 15.40, а), В анодную цепь лампы включены индуктавиость L и источник э. я с. Е. В сеточной цм1и имеется колебатеяьный коюур, состоянщи из индсгивностн L, магнитно связанной с Le, активного сопротивления R л емкости С.

Выходными зажимами генератора являются зажимы индуктивности La- Напряжение на этик зажимах по форме близко к синусоидальному.

Воспользовавшись методом первой.гармоники (см. § 15.47), определим амшипуз угловую частоту жтсколёбаний в схше рис. 15.40, а, когда се!вяаая характеристика лампы по форме близка: а) к жаригЛ

Его называют также ламповым ввтогенч1атором. Кроме схемы рнс. 18.-W, а с колебательным контуром в сеточной цепи применяется схема и с колебательным контуром в виодноВ цепн. Все выводы § 15.55 раепростраияютса и ва схему с колебательным контуром в зиодноВ цели.

кривой рис. 15.27 и б) к пунктирной кривой рис. 15.27. Эти i повторены иа рис. 15.40, б, в.

Составим уравнение.по второму закону Кирхгофа для мгновени-4 значений величин колебательного контура сеточной цепи, учтя, i

при выбранных положительных направлениях для токов имеет меспг! встречное включение нкпюсввзанных индуктивностей L и

(15.56)J

где с - напряжение на сетке лампы (оно же напряжение на емкости). 1

Из опыта известно, что ток i изменяется во вршени почти i гмоническому закону, поэтсшу положим 1=/ч,51п Л Тогда

~ = )/ cos SA\ с = rf = - /т cos а/ = - l/cm COS €0/,

где l/cm=/ >/fi C (ic=0).

Анодный ток является футжцией сеточного напряжения 1а = Пис)~] (рис. 15,40, б, в). Так как зависвмосгь ie=/(uc) однозначна, то пер-f вая гармоника тока ij, т. е. - /. cos находится в фазе с первой 1 гармоникой uc = - fcm cos Л I

Производная dxjdi уравнения (15.56) может быть найдена следую-1

вдим образом: --- = -1-.--. Но

(15.57) !

где S -крутизна характеристики лампы по первой гармонике. Ее j находят графическим нлн анал1ггическим путем по характеристике J <. = /( с). придавая различные значения. Каждому значению соответствует некоторое l/cm, а значит, н некоторые / и S. В свою \ очередь.

На рис. 15.49, г, d изображены завнсимосга S=f{I ), соотчегстг вующие рис. 15.40, б, е. Для рис. 15.40, г с ростом/ уменьшается S вследствие насыщения (нз рис. 15.40, б видно, что при больших uc анодный ток почти не увеличивается с ростом uc). Зависижють S= = /(/m). изображенная на рис. 15.40, d, имеет другоц характер: сначала S возрастает вследствие Перехода на более крутой участок кривой i =f(tic) рис. 15.40, в, а затем уменьшается вследствие насыщения. Подставив найденные значения dijdt, uc и тока i в уравнение (15.56), получим

(.L-JJ) co. <+(R-

j/mSinOJ/iO.

(15.58)

Сумма -двух функций, одна из которых изменяется во времени по закону сш, а другая- по закону косинуса, равна вулю для любого момента вршени. Это может быть либо в случае, котда / = 0 (коле- бания отсутствуют), либо ври/ =? О, котда выполняются два условия:

ыЪ=\1(ьО: (15.59)

R = MS/C. (15.60)

Из (15.59) следует, что угловая частота авижолебаний

ш=1/У£С. (15.61)

Иоследуе*. услсжия возбуждения колебаний, используя (15.60). С этсА целыо лостроим зависимость левой и правой частей (15.60) в функции от -рис. 15,40, с, ж (рис, 15.40, е соответствует рис. 15.40, г, а рнс. lS.40, же-рис. 15.40, д), полагая, что изменяется J?, а М и С несэменны. Сопротивление R не является функцией амплитуды тока fm, поэтому левая часть (15,60) представляет собой прямую, параллельную сси абсш1сс. Чем меньше R, тем ниже расположится прямая. Правая часть (15-50) -крия. подобная кривой рис. 15,40. а нли кривой рис. 15,40, д.

При Кг>й, прямая не пересекается с кривой, поэтому колебания отсутствуют. Колебания возбудятся при RRs. Рнс. 15.40, с иллюстрирует так называемое мягкое возбуждение колебаний, когда пМ1 уменьшении R амплитуда тока / плавно увеличивается начиная с нулетого значения. Рис, 15.40, ж иллюстрирует так называемое жесткое возбукдение колебаний, когда при плавном леныишни R амплитуда / скаЧком увеличивается с нуля -до некоторого относительно большого значения, например арк R=Rt до С а при RR, до Г .

Аналогичным образом могут быть рассмотрены условия возбуждения колебаний, если оставить неизменными R к М и изменять С или если RkC н 1зменны, а меняется М. Правая ветвь кривой рис. 15,40, ж соответствует устойчивым колебаниям (вычерчена утолщенной линией), левая -неустойчивым колебаниям (левая ветвь кривой является на-бочен ве1вы(4. Для токов и напряжений сеточной и анодной цепей (дли их первых гармоник) могут быть построены векторные диаграммы Мя действуюцрос значений первых гармоник (рис. 15.40, . Уравне-

вию (15.56) соотвегстнум уравнение в ксмгекксах

(1В.62)

Дня ьпткжшиых значений взменяющихся во времени величин аиоджж цепи (постоянная составляющая зджа ( напрйжения и. и достеянная э. д. с. £, ш учитываются) аф№ед;шво уравнение

-§-f+ -+ = 0-

Ему соответствует уравнение в комгепенсах

/wl.,/. - /о)М/ + i,R, + f?, = О. (15.63)

где -активноеатротнвлашеиндуктииюста Ся-комплекс первой гармояйки анещного напряжения.

Энертия иа псжрытне потерь в сеточной цепи доставляется иэ аноаной цепи вследствие наличия магнитной связи между ними.

Воздействие выходной цепи (в данном случае анодной) на входную тпь (в рассматриваемом случае ва сеточную) называют обратной связью. Обратная связь является необходимым условием гущестеовшшя автоколебаний.

в 2040 ВО ВО Jb

вшей юрввдичешоа ввигуждающеЙ , пж кторт амплитуды окон н наяркжеамй в цгои периодв-пп без воздиПствия ииешнето модулврующетв фактора. Аетомоду-Еследспшр веуст ------------..........--------- - -

рнс. 15.41, а с-яелвкеВвой емкостью, кулон-вольтную кара ктернсгн к у которой в соответствии с §15J!6 выразим в ввде t.c=ftshp?-

Т к как в цепи действуют посгояиная £, н синусоидальная £ ып (©(+ш\ S. д. с, то заряд q имеет ностаякную и скиусоидялытую коипонешы: д =

Пйстошная соскавляшцая

(co= sbp?e/.(?,0;

шрия гармшнна тока (i,=uft eo w(.

Еслн в ураииеиие цепи , *

с sin (шг-Ьч )

подставить яаписаниые выражения для у t/-+Uc, н райять его в соответствии с методом гармонического Саланса на уравнение для постоянное состявля-ющеЙ, для сикуеиой и косинусной компонент, а затем два носледних уравнення возвести в квадрат и сложить для устранения угла то, введя ( означения

i=pE /(<flL). b=Rlu>L, с=2соМаЦ: PQ =n. PQ =m. nMj-qHM два следующих уравнення:

а&Ъ nJ,{fm)=Eo=Uci. (я)

6*т*+ iJi (/йО ch n-mP -Л (б)

Разрешим (б) относительно clin:

Уравннше (в) дает связь ыежду пят. отасменную парамтрамп цеяи по lepBofi гармпшве частоты tn. а ypsHHetaie (в) но ностоянной составляющей. На рнс. 15.41, в изображена замкимосп, я от т. построенная по соотношению (в) при 0=0,5; йе=0,1; =в,. Верхний участок кривой сосаветстВует знаку плюс, а 1шживй-знаку минус веред раднвало в формуде (в).

ЗадараЯ1:1Ь аивчеивями а в нитвале 0-6 и беря соответствующие им значении i нэ рис. 15.41,6, по 1юрмуле (а) строим зависимость PQe=/(t/c(/a) (рис. 15.41.. Из рисунка видно, что в области значений 1/(уа=35-5-60 имеется пдвакииий участок, ве прикрытый восходящими учаетаами

Если EV будет такова, что изображающая точка окажется на падаю-: рнс. 15.41, в, то режим вынаденвые к -- - *

щем участке-

в етстеме начнетсй процесс аетивддуляции. Последний

SjCT иргаквжж yraofiwBiw, тал юк лля него имеется единственный предельньД

На рис. 15.41.* б. в пунктиром показано, *

т. Стрел!------- ---------

, (первой

гармоники TDSa t).

§ 15.57. Определение феррорезонансных цепей. Рассмотрим ipjumy юволшо грубых птшт, которые имеют место в ишях, оздержащих елиную тщщшжктъ и линейную шкость; такие цени тява феррвр&онаишши. Анаяшичньге яачения имещт место в цепич- левей-ной шщукзиввосшо в нешиейшш ш1ыо.

Для анализа ззик явлений можно воспольаовяться метедюм nefMi гарманики (см. § 15.47) или мегсррм расчета по дейсттоаим значениям (см. § 15.48. В § 15,53- 15.61 будет хфяменен метод расчета ло дейстишщиы значениям. Прн ом будем пользоваться в. а. х. нешшшдой индуетивнееш для дшствующих эначмшй тока и иач)я-ження. В этом методе в действительности еая1усоядааьн1 к ттл и напряжения тамеа1Ж01г их твшюхттмт сиябоот;да1Шнв вешчи-нами (зкмваяешиюея. в смысле де*ству1етдего значения ве § 7,12).

Когда п § 15.58-15.61, 15.64, 15.67 товоршся о савиге яо фазе между ткяш и взкфяжениая на кавом-либо эяемеяте схемы, то под ним понимают у-гол между экв[шалентаым син>*соидаяьиым током и эквивалешным сжусоимшшм напряжещюм.