W ?вх -вводное сопротивление днухполюашка по опюшению к зажимам аЬ; сопротивление ветви аЬ. Уравнению (б) отвечает эквивалентная схема рис. 1.30, о, где вместо двухполюсника изображены источник э. д. с. = н сопротивление R (схема Гельмгольца -

Тевенена).

Совокупность э.д.с. £2 -(/дб, , и сопротивления можно рассматривать как i[eKOTq]biii зквиеалснтшй генератор (R, является его внутрагним сопротивлением, а и ь X.. - егоэ. д. е.). Таким образом, по отно-л II /-аЧг rto h шению к выделенной ветви

УсШ 11* I If (ветви рис. 1.29. > всю ос-

тальную часть схемы можно заменить эквивалентньм генератором с названными значениями параметров.

Метод расчета тока в выделенной ветви, основанный иа замене активного двухполюсника эквивалентным генератором.

принято называть методом жви

ного генератора, методом ак-

тивного двухполюсника или методом хо/юстого хода и кор(ткого замыкания ,

В дальнейшем чаще используется первое название. Последовательность расчета тока этим методом екмдаидуется такая:

а) HaiiTH напряженке на зажимах разомкнутой ветви оЬ;

б) определить входное сопротивление R всей схемы по отношению к зажимам аЬ при закороченных источниках э.д. с*;

в) подсчитать ток по фсч)муле

(1.38)

Если сопротивление ветви аЬ равно нулю (R = 0), то для нее имеет место режим короткого замыкания, а протекающий по ней ток есть ток короткого замыкания (/j,). Из (1.38) при /? = 0

(1.39) (I.4G)

Из формулы (1.40) следует простой метод опытного шредвления входтго сопротивления. Для этого необходимо измерить >1апряжение холостого хода на зажимах разомкнутой ветви ((/ ь.) и ток короткого замыкания (/ ) ветви, а затем найти как частное от деления t/ Sx.< на

R =VaM,lIlK.

Если среди нсгочгнкпв пнтаиля схемы есть источники тока, то при определении входного гопротнвления всей схемы по отношению к зажимам оЬ ветви с источниками тока следует считать разомкнутыми. Это станет пояятаым, еслн вспомнить, что внутреннее сопротивление источников тока равно бескомчвосп (см. § 1.2).

Название метода-метод холостого хода и короткого замыкания - объясняется тем, что при решении этим методом для нахождения используется холостой ход ветви аЪ и для определения входного га-противления двухпсшоашка может быть использовано короткое замы-кание ветви ао.

Заменив источник э.д.с. ИСТОЧИИКОМ тока, получим CXeMV ЧКНЯ.ЯЛРитплт

генератор вще ряс. 1.30. 6 (схем. Нортона). аквявалентного

Пример 15. Определить ток в диагонали аЬ мостовой схемы р.с1Д о, пс агая ,= . = 1 0 ; .-4 0м: Кз = 2 Ом; .4о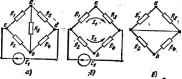

Рас. 1Л1

Решение. Размыкаем ветвь аЬ (рис. 1.31, б) и находим напряжение холостого хода:

У..... = 9 -Ф. = £.( = 10 (4г-гр) = 4.67 В.

Подсчитываем входное сопротивление всей схемы по отношению к зажимам аЪ при закороченном (кточннке э. д. с. (рис. 1.31, в).

Точки end схемы оказываются соединенными накоротко. Поэтому

Определим ток в ветви по формуле (1.38):

- .ь J(Rb+Rm) = 4,67/(2 + 1,47) = 1,346 А.

§ 1.27, Передача энергии от активного двухполюсника нагрузке

Если нагрузка R подключена к активному двухполюснику (см. рис. 1.29, о), то через нее пойдет ток IVm J(R-\-Rui) и в ней будет выделяться мощносп}

<!. )

- Выяснвм, каково должно быть соотношение между сопрмтшлением нагрузки R и входным сопротивлением двухпошосника Rt, чтобы в мпроплленни нагрузки выделилась иксимальиая мощность; чему она равна и каков при этом к. п. д. передачи. С этой целью определим первую производную Р т R и приравняем ее нулю:

dP +Д..>-ЗД(В+Д.ж) R-R .

(1.42)

Нетрудно найти вторую производную и убедиться в том, что она отрицательна <oJ, поэтому соотношение(1.42)соответствует максимуму функции Я=/(/?).

ГТодставив (1.42) в (I.4J), получим максимальную мощность, которая может быть выделена в нагрузке R:

P.. = ifi,J . (1.43)

Полезная мощность, выделяющаяся в нагрузке, определяется уравнением (I.4I). Полная моцуюсть, выделяемая эквивалентным генератором.

Коэффициент полезного действия

(1.44)

Если R = Ra, то 1=0.5.

Если мощность Р значительна, то работать с таким низким к. п. д., как 0,5, совершенно недопустимо. Но если мощность Р мала и составляет всего нескатько мил-тиватт (такой мощностью обладают, например, различные датчики устройств автоматики), то с низким к, п. д. можно не считаться, поскольку в этом режиме датчик отдает нагрузде максимально возможную мощность. Выбор сопротивления нагрузки R, равного входному сопротивлению И, активного двухполюсника, называют согласованием нагрузки.

Гример 16. Ham и, при каком значении сопротивления- Rs схемы рис. 1.31. а в нем выделяется максимальная мощность и чему она равна.

Решение, Из условия (1.42) находим: / = Л = 1.47 0м; P = t/As,../4i? = 4,67V{4-1.47) = 3,71 Вт.

§ 1.28< Пдкдача анергии по линии передачи. Схема линии передачи алектрической энергии изображена иа рис. 1.32, где С/ -напряжение генератора в начале линии; - иаприжение на нагрузке в конце линии -сопротивление проводов линии.

При передаче больших мощностей (например, нееколькия десятков мегаватт) в реальных линиях передач к. п. д. состашгае!- 0,940 97, а бз лишь а несколько процентов меньше (У,. Ясно, что каждый процент повышения к. п. д. при передаче больших мощностей имеет существенное экономическое значение.

Характер изменения мощности в начале линии Р мощности в на-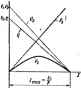

грузке Р к. п. д. ч и напряжения на нагрузке f j в функции от тока ио линии при неизменном напряжении на входе линии и неизменном сопротивлении проводов линии R иллюстрируется кривыми рнс. 1.33. По оси абсцисс на этом рисунке отложен ток /, по оси ординат-Р,. Р и,. 1).

Максимальное значение тока имеет место при корот-

ком замыкании нагрузки. Кривые построены по уравнениям P,=Uil; P,UJ-m,;

j; /.=(/.- ./.

Если no линии передачи с сопротивлением R, и сопропвшением нагрузки R должна быть передана мощность

P.-I-R.. (а)

то к. п. д. передачи тем выше, чем выше напряжение (/ в начале

Выждем формулу, показывающую, как к. я. д. шеисит от напря. гездм определим R, = Pjn, ио 7 = Uj(R, + RJ,

Разрешим (б) относительно R, [анан минус в формуле (в) перед корнем тброшеи, так как он соответствует правой части ививой Р. - = /0 с мевыитщ]: 1 s

Таким обрадом.

.) + /(ГД- .Г- 2- (в)

ь , миарическая схена>, узел

а.. 2. Как выбирают вож

i. Определите понятия лектрическг ветвь , источник э. д. с... источник i

направления для такое ветвей, как связаны с ними положительвые иапр напряжений на сопротивлениях? 3. Что понимают под в. а. х.? 4. НарнсуЙгя в. а. X. реального источника, источника э. д. с. источника тока, линейного сопротивления. 5. Сформулируйте закон Ома для участка цепи с э. д. с. гервы! и второй законы Кирхгофа. Запишите в буквенном виде сколько ург дует состаилятъ по первому и второму законам Кирхгофа- 6. В напряжения от падения напряжения? 7. ОхврактериэуЕте основные этапы метод контурных токов (А1КТ> и метода узловых потендиалов (МУЛ). Прн каком уел* ВИИ число уравнений по МУП меньше числа уравнений по МК.Т? 8. СформудН руйте принцип и метод наложения. 8. Запишите и поясните линейные соотношу НИИ Б электрических цепях. 10. Что понимают под входными и взаимными пр водимсчяями? Как их определяют акалкмческн в как-опытным путем? ii. кажите, что метод двух узлов есть частный случай МУП. 12. Приведите i. показывающие полезность преобраэОБання звезды в треугольник. 13. Сформулируйте теорему комненеацнн и теорему вариаций. 14. Данте определение актив:- ввухполюсннка, начертите две его схемы замещении, нвйдите их параметры, речислите этапы расчета методом эквивалентного генератора. 15. Запишите уело вне передачи максимальной мощности нагрузке. Каков при этом к. п. д.? 16. Рь шите задачи 1.2; 1.7; 1.10; 1.13; 1.20; 1.24; 1,33; 1.40; 1.41; 1.45.

электромагнитная индукция. индуктивность и емкость как параметры электрических цепей

§ 2.1. Явление электромагнитной индукции. Электрические tokit создают магнитное поле. Вкаждой точке оно характеризуется вектором магнитной шщукции В и ндоряжсешостью магнитного поля Я, которые связаны соотношением B - \iH, где i, = Poti -зйсолютнау магнитная проницаемосгь; Р(=--4я-10 -магнитная постоянная, Г/м.

Единицы измерения: [B] = BCJm~B6/m, [ j=A/m.

Магнитному полю присущи два проявления -силовое воздействие иа ток (па движущийся заряд) и наведение э. д. с. В основу опреде ления вектора В положено силовое проявление магнитного поля. Ин дукцию в определяют как силу, действующую на проводник единично длины с током в I А, располонФнный перпендикулярно вектору fl (см. § 14.1), Напряженность определяют как разность двух физических величия: Я = (В/Ро) - J* где /- магнитный момент единицы объем i вещества (см. § 14.24). Потокектора В через поверхность S называктг магнитным попшом Ф = J В d5; [Ф] = В - с = Вб.

Явление электромагнитной индукции было открыто в 1831 г. английским ученым Майклом Фарадеем. Суть явления в том, что при изменении магнитного потока, пронизывающего какой-либо контур (обмотку), независимо от того, чем вызвано имленшие нотжа, в контуре (обмотае) наводится электродвижущая сила £.

Опыт показывает, что наведенная э. д. с. пртло пропорциональна

скорости изменения потокосцепления контура

(2.1)

Потокосцештение контура i]) равно алгебраической сумме потоков, прса!изывагощих отдельные витки обмотки:

1= Ф,+Ф, + Фз + ...4-ф . (2.2)

Если все витки обмотки w пронизываются потоком Ф, то

= tb. (2.3)

Так как ш-безсазмериая вешмша, то iJj измеряют в тех же единицах, что и Ф. Важно об-

вщр

ратить внимание на еле-

1лй веедеийой э.9,е,.

1) if-это полное или результирующее потоко-сцепление контура (обмотки); оно создается не только внешним по отношению к данному контуру потоком, но и собственным потоком, пронизывающим контур при протекании но нему электрического тока;

2) знак минус объясняется тем, что положительное направление отсчета для наведенной э. д. с. и положительное направление линий магнитной индукции, прони-зывающих контур при возрастании потока, принято связывать

правилом правого винта: если закручивать правый винт так, что его острие двигается по направлению магнитных силовых линий при возрастании потока, то положительное направление для наведенной э. д. с. совпадает с направлением вращения головки этого винта.

Знак минус в формуле (2.1) поставлен с цечью приведения в соот-вегствие действительного (попучашого из опыта) направления э. д. с. лри оговоренных условиях с направлением отсчета, принятым для нее за положительное ()ис. 2.1, а).

Формулу (2.1) иллюстрируют рис. 2.1. б. в: на рис. 2.1, 6 показана зависимость потока, пронизывающего одноаитковый контур Р*- 2.1. о от времени: Ф=/(/); на рис. 2.1. е - зависимость э. д. с. -/(0. иаводамой в контуре, от вршени.

Свои эксперименты Фарадей проводил с замкнутыми проводниковыми контурами. Наведение э. д. с. он объяснял как следствие пересе-*ения приводами контура магн1гтных силовых линий.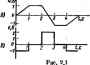