грар8ще й; (/,-)-Дн,-Ь(; -Диа=£. Еелн в-последнем уравнениязаменить ва £, то окажется, что tie

йи-1-ДИе=0. (15.51J

где Дыд-прнрйщеиие напряжения ие нагрузке р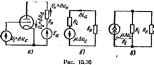

cypai

мне (15,51) вместо Ди подставим /; н вместо ДИд в соот (15-50а) подставим ,Д -цДы- Получим

( ..+й)Лг =МЙ с- (1В52)

.У11авнению (15.52) отвечает схема рнс. 16.30. б. В этой схеме к источнику в. д с. цДня присоединены сопротивление нагрузки в внутреннее сопрогивле-иие электронной лампы ft,. Таким образом, для мвльи приращй анодамо цепь ЗЛ1ГТР0ННОИ лаиш! замещаюг (имитируют) источником э. д. с. цДи в последовательно с вим включенным .против-

! ftl-Э.Д.

источника

i лвмпы (т. е. это эавн-1НКЭ.Д, с; ср. с 5 15.35). рнс. 15.30, в изобракена а схема за-

вня Hi

СИ11ЫЙ

Другая , ... у,шл,свиа скеиа замещения. В ней вместо источника э. д. с. включены источник тока V-fuJRi и шунтнрующее его сопротивление ft, (напомним, что иереход от исТ1эчвнка э. д. с. всточывну тока рассмотрен в § 1.2).

В cxeftMX 15,30, б, в ие учтены мея!элапрсдные рмкости, поэтому такие схемы применимы для относительно низких частот. (Схема замещения для высоких частот изображена нз рис. 9.3, б.)

Щкяер 154. Между сеткой н като-

Решение. Определим пол(нкенне рабочей точки на вдактеоиствках лзмпм с юн крнаов семейства, для которой параметр ,= 2 В. Itowoiai

PHt 15.31

> - nun (.(часмсгаа, для КС

точки; ц,=94 В и i,=3,67 мА.

По определению (см. <]юрмулу (16.46. яхя яахшкдвиня gt следует, считая se исходное положение найденную раСочую точку, при ненамеином ((с=-2 В дать приращение анодному напряжению Aug, найти соответствующее ему приращение анодного тока Д1д и разделить Aij, на Au:

S,=dijdu,

чДг./Дн,=5 мА/50 В=10-< См. ft£=l/g,=10 Ctei.

лона ивсатеяыюй в ра-

бочей точке к кривой

Для определения ! . .

сеточномр напряжению Auc=-1-(-21 = ствующее ему приращение Дя=4,б7-3,67 saAi,/Ao,=10- А/В. К< дальней состввляюшсй то

S при Ыо=94 В даем приращение и из рисунка находим соответ-1 мА. Следовательно, S=dyaucsa 4яциен1 усиления p=Stej=10. Амплитуда снвусои-в ашшной цепи согласно (15.52)

Анодный ток ia=3.67 + 0,02 6inti>f мА.

S 1£.42. Поармвце axauCHitocTii вход -выход для ампроииой лампы пря больших сигналах. Напряжение между сеткой в катодом щ является входным, а напряжение на ,нагрузке R (см. рис. 15.30, а)-выходным. Напряжение на нагрузке равно пршэиедению тока i на аяютавлаше Rn- Если амплитуда переменной .составляющей иапряженин и, достаточно большая (например, соизмерима или больше посгояквпй (оставляющей напряжения Uc), то линейные схемы замещения рис. 15.30, б. в применять нельзя. Опрцделеиие завмсаиоств тока i, от временя ( при подаче на сетку лампы напряжения любой формы и любой амплитуды можно пронжщвть путем графических построений. Сущность последних состоит в следующем:

1. Придавая времени / различные вначенвя, находят отвечаюпхие им мгновенные значения и.

2. Для каждой нары соответствующих друг другу значениВ f н инодный ток ij определяют ординатой точке переседеиня кэпуэочноЯ пряней и той крявоИ семейства ie=f ( а), для которой данное значение Uc является параметром.

3. Строят кривую зависююств (g=f(Q. Рааложение ее в рвд Фурье позволяет найти постоянную составляющую, а также амплитуду первой в высших гармоник ряда Фурье. Повторив лостроення при нвой амплитуде или иной форме напряжения ti определяют новые значения постоянной составляющей и амплитуд первой ш ВЫСШИ1 гарыоннк тока 1. В результате ряда таких построений получают данные, иа основании которых .можяо построить любые представлякщне интерес Зависимости иежду входными и выходными величинами. В прннпнне аналогичные построения могут быть проделаим и для транзистора.

§ 15.43. Тярястор-управляемый лолуфоввдэвкоБый днод. На рис. 15,32, с изображена простейшая схема включения тирнстора. Тиристор -это че1ырехслЫ*ный полуправодник<Ж1Ш прибор с тршя р-п-переходамй (/, 2, 3). Напряжения иа них обозначены Ui, щ, Ид; в. а. X. р-п-пЕреходсш 1 и 3 изображай иа рнс. 15.32, &, в. а. х. перехода 2-на рис. 15.32, в (включет всхретао р-й-пфеходш /и. При *= з 8 переходе 2 происходит лавинная имшзащтя .(пунктир па рис. 15.32, в). Суммарная в, а. х. трех переходов i >=/( ). т.е. Ч. а. X. всего тиристора, нзсажена на рис. 15.32, а. Ctea шмучена сложением абсхщсс рис. 15.32, в в двух абсшюс рнс. 15.32, 0. Участок 1 - 2 ий ией соотаетстет участку лавинной нонизацин вхсго ;7-я-перехода.

Если 1фн замкнутхж кж)че К рнс. 15.32, а э. д. с. Е CTMier немного больше тиристор зажжется, т, е. перейАвт в открытое ,

состояние. Ток в цепи станет равным току ip на рис. 15.32, а. Прямую / на рис. 15.32, д называют нагрузочной. JXna погашения тири- стора необходимо, чтобы ток через него уменыпнлся до t<i; (рис. 15.32, г). До сих пор речь шла о работе тиристора в режиме отсутствия управляющего сигнала (так работает тярнстор -см. § 13.2). При воздействии управляющего сигнала (импульса тока или напряжения) на управляющий электрод (расположенный вблизи р-п-пере-хода 2, см. рис. 15.32, а) от вспомогагельной цепн, пе показанной на рнс. 15.32, о, П11оисходит лавинная ионизация р- -перехода 2. Подавая импульсы управления, гюжно снижать на1фяжепие зажигания (т. е. зажигать прибор при более низксм и ).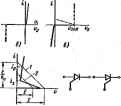

6) е) д)

Пунктиром на рис, 15.32, д показано положение нагрузочной прямой 2 в управляемом тирасторе. Переход от закрытого состояния к открытому прсякхоцит за дати микросекунды. Тиристоры выполняют на токи от датей мнллиа.мпер до нескольких килоамп!. На рис. 15.32, е, ж показано условное изображение тиристора на схшах.

PjK. 15.32. е соответствует угфавлению тиристором со стороны анода, рис. 15.32, ж-со стороны катода.

§ 15.44. Общая характеристика методов аналяза н расчета нелинейных электрических целей переменного тока. Анализ нелинейных явлений и получение числовых соотношений в нелинейных цепях перв*нноготока являегся более сложным и трудоемким, чем анализ м расчет линейных электрических цепей.

Как правило, в нелинейных адектричесннх цепях содч)жатся либо нелинейные индуктивности, либо нелинейные аякостн. либо безынерционные в тепловом отношении нелинейные активные сопротивления. Токи и напряж0шя в таких цепях в ТОЙ нли иной степени несину-сочдвльны.

Т<жи и иапряжения в большей cten iH синуооидалмы в цатяя содержащих только инд)ционные в тшлсшоч отношении нелинейные активные сопротивления.

Все методы анализа нелинейных цепей можно подразделить на две большие группы; аналитическую и графическую. Аналитические методы в отличие от графических дают возможность проводить анализ в общем виде, а не только для частных значений параметров.

Недостатком аналитических методов является то, что приходится выражать аналитически характеристики нелииейпгх сопротивлений; а это всегда связано с некоторой пограшюстью. Расчет сколько-нибудь сложных нелинейных электрических цепей перетленного тока можно произвести лишь с известной степенью приближения.

Наиболее широко распространены следующие методы анализа и расчета нелинейных цепей переменного тока:

1) графический при .использовании характеристик нелинейных сопротивлений для мгновенных значений;

2) аналитический при использовании характеристик нелинейных сопротивлений для мгновенных значений при их куточно-линейноЙ аппршсимации;

3) аналитический нли графический при использовании в. а. х. по первым г)моникам;

4) аналитический или графический при использовании в. а. х. по действующим значениям несннусондальных величин;

5) анзлштеский путш расчета по первой и одной или нескольким высшим или низшим гармо]1икам;

6) с помоп11.ю линейных схем замещения;

7) малого параметра;

S) интегральных уравнении; 9) кделирования на моделях.

В дальнейшем кратко охарактеризован кажщй метод. Тот или иной метод целесообразно применять в зависимости от характера цепн, формы в. а. X. нелинейного сопротивлшия, а такжеот того, какое нелинейное явление в цепи исследуется. Чем сложнее характер нелинейного явления, тем более сложным и громоздким оказывается метод его анализа. И, наоборот, анализ грубых нелинейных явлений производится более простыми средствами.

§ 15.45. Графический метод при использовании характеристик нелинейных сопротивлеыий для мгновенных значений. Экп метод применим, как правило, к цепям, в которых известен закон изменения во времени какой-либо одной определяющей работу велв-ивого сопротивления величины, например тока, напряж.ения, заряда.

Последовательность, расчета данным методом такая:

1) исходя из фпзиче<жнх предпосыжж, положенных в основу анализа, находят закон изменения во- времени одной из определяющих работу нелинейного оопрогивления величины;

2) используя характеристики (характеристику) нелинейного сопротивления для мгновенных значений, путем графических построений

иаходнт знкин иаиенеганя ва времени второй величины, onpenejraK 4-j работу нелинешюго .соиретивлшия;

3) по результатам п. 2 путем вспомогательных графнчеошх строений и жростейших ;расчетов находят выходю величину я иск мое аэотношевие между параметрами схемы.

Достоинствами метеда являются гфостота и лагаяднестъ, а так-i легкость учета гнстерезисных явлений. Пример ш. s § 15.8и J5.2*

§ 15.-46. Аналитический методдри использовании характежстма нелинейного опр0131влеиии для мгновенных значений лри их к* сочио-линеииой аппроксиманни. Основным содер ляется caei

метода

е-задачи о -нтаождении периоди%скога решения -н--

нейных уравнгаий ж нахождению периодаческих) раншия сисгел линейных уравнений.

Основные -эташл мещца следующие:

1) замена вольт-амперной (вебер-а1)ше{жой, кулон-вон>тной) харм теристики нелинейного сшротивления -(нелЕшйтнсто элемента) дл мгнсжерных значений отрезками ipniix яиний;

2) подстановка в нелинейные дифференциальные уравнений yji неияй прямых п. 1 (этим ненинейные диффе5)а1циальные уравиенв будут сведены к линейным). Каждому нел1шейнсту уравниипо буч соответствоБать столтжо линейных уравна1ий, сколько отрезков пр<ч мых заменяет характеристику иелинешкжо сопротивления (элемени<

3) решение свстемы линейных дифферешогальных уравнений Каждому лииейнсФяу участку характфистики нелинейного conpoPin ления будет соогветсгеовать свое решение со своими тгастояниым интегрирования;

4) определение постоянных интегрирования всходя из соглгсоввни решения на одном линейном участке с решением на другом линейно* участке.

Hffli6onee эффективен этот адетсщ, когда характеристику пепине ого элшешта х ижестной -степандо приближотя можно замен i отрезками прямых, раснсиюжа1вых таким -образстл, что когда сщ велнвдна, определяющая режим вб&т неяинейикх) адеаапа, напр, мер тсж, меняется, во другая, например погсжосцеплевие, нежмиш

Еще более эффективен метод, если отретси пряаых, зан€иякщ в. а. X. нелтшйного элемента, могут быть взяты совнадающими с осям координат.

Пример решения -задади для этого случая ем. в § 15.51-ь1Ё.

§ 15.47. Анаи

4Й (1рафическнй) метод расчета но иервм! гармгашкам 1шов и т1фяженн9. В moti методе по сложному зако* изменяющиеся токи и напряжения на нелннЫЬк ! сопротивлении заи-няют их первыми гартданнками. В расчете используют ъ. а. х. п первым гармоникам в анал№шчесной форме или в вцде графическо завнстюсти.

Основные этапы расчета -в аналитическом варианте: 1) выражают аналитически в, а. х. нелинейного -оопрогнвлен для MTHOBOQftjx значений;

2) щтш подстановки в нее пфвой гармоники напряжения или тока получают формулу, которая дает нелинейную связь между эмиялудой первой гармоники тока через нелинейное сшротивляше и амплитудой первой гармоники напряжения на нем [И качестве мера такой связи можно назвать формулу (15.19)];

3> в уравнеиш, составленное для иа!ле;шой цепи по второму зако! Кирхгофа, подставляют вместо мгновенных эвачетФ тока и иахжеяив на негаягейном сопрогивлшии мгжжйшые значения их первых гармоник, а высшими гармониками пренебрегают;

4 уравншие раэ&шаот на даа уравнения: одно и них выражает собЕШ- равенство- к(йффишшчш при- синубяых елагаешх лшй? и пршой частей уряшкння, дгое-равенство коэффициентов, при коеи-HyoHJX слагааиых обеих частей уравнения;

5) прсжзводят совместное решение этих двух урашёний;

Овюные зетапы расчета в графческсм- варианте

1) в качестве задисимости между ашипудой первэй гармсяпиш-на1фяжения на нелинейном сопропшлмшн и анняшдсй первой гар-мшнки тот чфез него берете нелиншная зависимость в- виде графика, Эса завнашость может- быт& nojqaia любым путш, в. том чися& W опытным;

2)- преютолыго задшотся амплитудой 1, nq)BOH гшоннки тока через нелннное сопротшлида нз графика находит сеютиетствукда ей амплиэуд первой таркюники напряжения на нелинейном сопро-тив;;ении и гатем путем построении векторной диаграмчы но -первой гармшмж для к:ей схемы- определяют амплитуду t/j первой гармоники натфиження на входе- схетш, Поороение вектной диаграммы прсжжодится: ТЭК жб, кэк И ДЛЯ обычнык ляншых цепей синусои-дажлои). тежа а именно: если ие учитывать потерн, в сердеяннке, то первая- гарноаша напряжения на нелина1ной нндуишшисти oiffipe-дсает ифвую гармонику протекшощего чеэ нее. тока на 90, первая гармоника напряжапш на нелшжнлой шкосш отстает от протекающего через нее тока на 90 ; пфвые гваоники напряжения и тока на вежшейнсм активном сопрогявлиши па фазе ажгшдают;

3) путем построения нешолышх векторных диаграмм для различ.-ных значений- /, находят соответствующие нм Uj и строят в. а, х. всей схемы t/in./{/i )-

Данный метод позволяет исследовать такие нелинейные явления, как. преобразовагаж поегоягаюго тока в пеменный и обратное пре-оазоваяие, вдление резонжса на осгожной гармонике, триггерный эффект на nq)BOH гармонике, некоторые типы авгсжюдуляцнонных процессов. Но он не пожоляею исследовать более сложные явления, как, например, резонанс на. иязпнх и низших гармониках, резонанс на фобных гармониках и др.

Если пользсжаться аналягаческим вгнашом этого метода, то решение можно получить в общем виде, что весьма существенно, так как становится возможным нсслецсюать ранение при измшеиии лкого из параметров цепи. Этот метод будет применен для Ш1алаза. работы автогшшора (см. § 15.5 и дли анализа разветвлешюй иепи с нелинейной индуктивностью (см. пример 159).