3. Путем ESMenetnn >о или можно изменять амплитуда первоП в esjcuvi гармоник фуширй у(м/)-

Первое вз этих свойств гоясним графически. Пусть нелинейное сопротнвленм работает при отсутствии синусоидальной составляющей (x =OJ. Тогда изображу! инем этого процесса вз характеристике нелинейного сопротивления будет точка (рнс. 15.13, а), Лля

Этот результат следует вз (15.12), если учесть, что Jo(0)=l.

(15.1*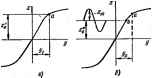

le.работает-при хфО, то, для т

постоянную составляющую функции сохранить прежней, постоянная составляю щаа Ха должна быгь снижена (или син31ггся сама) со звзчения х, до х. Постоянную составляющую pxj получим иэ формулы

я а (рмс-

где х1 определяется ординатой точки Ь, расположенное ниже точк

Первое и третье иэ этих свойств широко используют в теории упр. нелинейных сопротивлений, второе свойство-в теории умножителей-ча!

npHMqi ISO. Нелинейное сопротивление с характеристикой !/=as\ix

работало прн й/а=41,1 и отеутстии переменной составляющей lfix =0). ЗатЦ режим работы его изменился: постоянная составляющая yja осталась прежне! но появилась переменная составляющая амплитуда которой рх =4. Hafixi постоянные составляющие рл в этих двух режимах.

Решение. В первш режиме pjc;=Arsh 41,1=4.41. Во втором режиш

=Arsh 41 .l/Jo 0*4)=Arsh 3.63=2.

Таким образом, при переходе от первого режима ко второму

составляющая рхд изменилась с 4,41 до 2, т. е. более чем в два раза.

П. В энергетическом отношении общие свойсгеа нелинейной цепи, сцверж:

.. , ченную ицпукшвпхпъ (емкость) с характеристикой, в которой действуют генераторы синус*

и /я и возникают токи и напряжения частот Sm.n= ih+nh {tn n-простые целые числа; они когут принимать положительные, отрицательные нулевые эначения), для периодических процессов описываются теоре. иРоу.

Если через lPm.n=tm.n*m.n+t/m. /m. обозначить среднюю за перИ мощность, втекающую в нелинейную индуктивность (емкость) на ча(;тоте/т. zam/i+iB. то теорема устанавливает связь иежду мопшостями, Тжйядим. в нелинейный элемент вз различных частотах. Эту Teoi)eMy записывают в ъЛ

В (доказательство см.. например, в [21]);

1 li

(15.16)

\ постоявноб I

мстикой. Ecj

, потока.

§ 15.18. Г

неХу сопротивлению с симметричнойв. а. х-Тнапример iatP, поднести шпряжение в виде двух кишонент: K=t/ian raf+f/s йп (2а(+9), частоты которых относятся как 1:2 [в более общем случае как 2А/(2р+1), где k ир-целые положительные числа), то В токе, проходящем через НС. несмотря на отсутствие выпрямителей, появится постоянвзя сосгавлякжиая, равная-0,75 ota яп ф. Ее величина заввсит не только от н t/j, но и от угла ср. Сам факт возникновения постоянной составляюхцей в этих условиях называют сеяектиеныя выпрям-яеншм. Селективно оно потому, что возникает не при любом соотпошенни частот двух напряжений, а прн вполне определя(ном. Сходное явление имеет место Б нелинейных ивдуктнвностях к йюстях. Тик, если на нелинейную индуктивность с в. а. x. i=a;shp0 воздействовать потоками частот ч, и 2©, то при отсутствия постоянной составлякяцй в м. д. с. в потоке кроме указанных гармоник Появится и постоянная составляющая. Для ее опредвлення положим Ф=Фо + -(-Ф1Йп(ю(-{-9)+ФгЯп2т(, подставим в формулу для i в ряд Фурье, приравняем постоянную составляющую ток получим формулу для определении Фд;

нулю. В рельтате

где 6о=рФв; Ь,=р Если

§ 15.19. Тиоы характеристик нелинейных сопротивлений. При

анализе и расчете электрнчшшх цепей с нелинейными сопротивлениями в зависимости от рассматриваемого вопроса используют различные типы характеристик одного и того же нелинейного сопротивления: а) характеристики для мгновенных значений; 6) вольт-амперные характ)истики по пфвым гармоникам тока и напряжения; в) вольт-амперные характеристики для действующих значений.

§ 15.20. Характеристики для

значений. Основным

типом характеристик являются характеристики, свяалвакяцве мгновенные значения оаювных определяющих величин: тока* и напрнже-ния на нелинейном *активном сопрогивлапш, индукции и напряженности в сардечннке нелинейной индуктивности, заряда и напряжения ва нелинейной емкости. Будем называть их характеристиками для мгновенных значений. Иногда пфед этим названием добавляют соот-Еегсгвевно следукнцие слова; вольт-ампошые, вебер-амперные или кулон-волкгные.

§ 15.21. Вольт-ам

i характожстики по первым гармоникам,

Под в. а. X. по первым гармоникам понюлают графическую или аналитическую связь между амплитудой (действующим значением) пфвой гармоники тока и амплитудой (действующим значением) п)вой гармоники напряжения на нелинейном <

тип характеристик подраздеяяют на дв подгруппы. В первой подгруппе характеристик принимают, что напряжснн (поток или зарядО на нелинейном сопротивлении изменяется по сину соидальному закону.

Во вттЗрой подгруппе характеристик принимают, что по синус- идальиому закону во времени меняется ток через нелинейное актив ное сюпрсггавление (напряженность в сердечнике нелинейной ичдук тивности или напряжение на нелинейной емкости).

Если воздйнлвугощее на нелинейное сопротивление синуссждально напряжение (синусоидальный ток) не содержит постоянной составля Ю1цей, то в. а. х. для первых гармоник данного нелинейного сопр> тивлення изображается какой-то одной кривой. Если же воздействуп щее напряжение (ток) содержит посгояиную.сюставлякйцую, то волы амперные, вебер-ампернч или кулон-вольтные харак \f -. теристики изображаются се-

мействами кривых, на которых постоянная состав пяющая тока, напряжения потока нли заряда является параметром.

Этот тип хч)актфнсти1 получают расчетным (аяа лвгическим) или графиче) ским путем по- сосггветст вующим характеристика! для мгнсшенных значащ! Г, или снимают эксперимет-тально.

При графичеоом пост ш ...,.. роении задаются различны

ми значениями амплнтудн воадействующего на нелинейное сопротивление напряжения (тока, ин дукции, з)яда), по точкам строят 1фивую тока (напряженности, на пряжения) в функции времени и путем разложения ее в ряд Фурм находят соответствующие амплитуды первой гармоники тока (напря женнссти, напряжения).

(Пример г1)афического построения -кривой тока в функции времй для управляемой нелинейной индуктивности см. на рис. 15.17.)

Аналитически построение точек обсуждаемой характеристики прои! водят, используя формулы (15.12) н (15.13) и.чи иные подобные щ-В § 15.23 раалютраю применение формул (15.12) и (15.13) д.-получения единых характеристик по пфвым гармоникам для управл) ёмых симметричных нелинейных сопротивлений.

Для нелинейной индуктивности в. в. а. по первым гармоника! можно получить опытным путем при помощи схемы рис. 15.14. £ где WTi-источник силусоидалыюй 9. д. с, WT2 -источник постояв ной э.д. с, о(7 -зажимы управляемой цепн НС; cd -зажимы упрм ляюЩей цепн НС, Измерительный прибор Vi реагирует на nepeji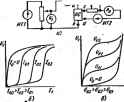

гармонику напряжения, а измерительный прибор i4j -на первую гармонику тока.

На рис 15.14, б качественно изображены В. а, х, управляемой нелинейной индуктивностн по первым гармоникам. Парам1тром на них является ток управления У .

В. а. X. по первьщ гармоникам для управляемой неяинейной емкости изображены на рис. 15.14, в. Параметром на них являегся управляющее постоянное напряжение U.

Снятие характеристик рис. 15.14, б производят следующим образом. Устанавливают некоторое произвольное значение тока в цепи управления, затем плавно повышают напряжение и для каждого его значения записывают величину тока /,. Затем то же проделывают прн новом значении / и т. д. Результаты измер№ий наносят на график, и соответствующие точки соединяют плавной кривой.

В. а. X. для первых гармоник используют при расчете установившихся режимов в нелинейных цепях, который называют расчетом по первой гмонике (см. § 15.47).

При расчете применяют в. а. х. той подгруппы, которая более подходит по условию работы данного нелинейного сопротивления.

§ 15.22. Вольт-амперные характеристики для действующих значений. Под в. а. X. для действующих значений понимают заетсимостъ между дайствующим значелием синусоидального (несинусоидального) напряжения на нелниейнсм топротивлетии и действующим значением тока, протимкааего через это сощхливление. Еслн напряжение (тж) содержит постоянную составляющую, то а. а. х. для действующих значений изображаются семейсшсяи кривых, на которых постоянная составляющая тока (потока, напряжения или заряда) является параметре !.-

Этн характеристики получают графическим или аналитмтеским путем из .хактеристик для- мгнсвашых значений или снимают опытным путем с помощью схемы рис. 15.14, а, но приборы У, и Л,-в этом случае должны измерять действующие значения.

В. а. X. для действующих значений зависят ог формы напряжения иа нелинейном сопротив;]сн11и и (нли) от формы протекающего чез него тока, поэтому необходимо указывать, при каких условиях они получены.

При качествшном н грубом количественном анализах полагают, что характеристики, снятые прн одной форме напряжения на нелинейном с№ротавлшни. близки к характеристикам, снятым при другой форме напряжения, В действительности же количественное различие в хактеристиках может оказаться значительным. В, а, х, для действующих значений используются при расчете, называемом расчетом по а, а. X. для действующих значший (см. § 15.4,

§ IS.23. Получение аиалнтнческнм путем о& емш иетиеЗных сопротивлений па первым га нелинейные индуктивности и емкости, а также б

пых сопротивлений имеют характеристики дл1 ......

могут быть прм&гашкенно описаны формулой у=в shpi. Для каждого нелинейного элемента пол х я у следует понимать свои величины (см, § 15.13).

Таким оазои. х и j/-обойтспиые обозначен первой гармоники функция !/

формула (15.1Я устанавли.... связь Mowy аишщдой Уш Р

И вжтудо i первой герковияв х и восто.ниоВ соствв.тющеИ х.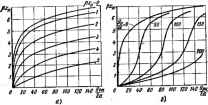

ш Наоис 1515, о нзображеиы характеристики управляе вте нелинейного 1ме-,:.tVW -(( . np/to-O, 1. 2. зГ4. 6, noctpoeHHuc по формуле (15.19).

nSbZS Hpi .-.. тном виаие ш,рамеч.а (ta. Если из-

нейного &ле-муле (15.19).

ЫМЙ можно -

н ке Вд:,- а сосгоязная составляющая ;, / . ceweftirreo кримх .lapa у ,а можег быть построено следующим образом. Hs формулы (15.12) находим

о сЬрлГо в (15.19) иодстжнм

Коивые рис. 16-15. б. построенные по формуле (15.20), явлвются характе-пиствканн управляемого иелнне1иого элемента при аначенилк параметра yla = L 50, lOo (50 и 200. Обратим внимание на то, что й /(2а). р* . Wa-o величины с нулевой размерностью. Если насилабы по осям уненышпъ в F 2 раз. то кривые рис. 15.15, б будут представлять собой характеристики по действующим значениям первых гармоник. Характеристика неуправляемого нелииеВпого элемента изображена на рис- 15-15. б кривой, для которой у,1а=0.

§ 15.24. Простейшая управляемая иелинЫ1ная индуктивность.

Простейшая управляемая нелинейная индуктивность изображена на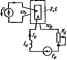

рис 15.16, Она состоят из о& тж w, и w, намотанных на замкнутый фч)ромагнтныа сердечник. Площадь поперечнсго сечения сердечника S (м, длина средней магнигасж линии I (м).

Обмотка Wi вклююна s цепь п)еменнога тока, и по ней проходит перачавпи ток i, содержащий первую и высшие гармоники.

Обмотка управления (подмагннчиванвя) w присоединена к источнику постоянной .д.с. Ео через дополнительную ивдуктивность Lg и регулируемое активное сопрогевлшие Яо- По обмотке Шд протекает постоянный ток/о = £о ?о

Хотя перемошьш магнитный поток и иа- р jp

водит в обмотке Wo переменную э.д.с но гуменного тока по ней практически не проходит,

так как дгаолнительная тщуктавность Lg образует для пжмениого тока дсстаточио большое и1щуктивное оопротивлетие.

Пусть прнложешюе к обмопж напряжение радио UcosaL Эю Напряжение равно э.д.с. самошщукции, взятой с обратным знаком (активное сопротивлЕние обмотки ш, считаем весьма малым):

u = -eL = Wi~ = UmCOS tut.

Отсюда мапнггный поток

=0 sincof-l-0 ; (15.2!)

Ф ==адйЫ (1Б.22)

где Фр, -амплитуда племенной составляющей магнитного потока; Фв постоянная составляющая магнитного потока.

Управляемая нелинейная индуктивность позволяет пут&и измеиеннн постоянного тока f в обмотке w управлять переменным током I.

Принцип управления режимом работы нелинейной индуктавности и характер нзмененця во времени отдельных величин поясним с помощью рис. 15.17, а, б, где кривые Ф=/(Я/} представляют ссбой зависимости потока Ф в сердечнике от произведения напряжвщоста магнитного поля Н на длину средней магнитной линии / сердечника,

Построения на рнс, 15.17, а соответствуют случаю, когда /о = 0. а на рис. 16Л7, б-когда 1 фО. На обоих рисунках перемещая составлякиея потока Фт51Псв/ одинакова. Для рис. 15,17, а постоянная составляющая потока Фв=0, для рис. 15.17.6 Фл=?*=0. На кривых Ф = К(оО. = f{fil) и ii!Ji=f(ftri) наиболее хч>актерные соот-ветствукшще яруг другу точки обюначены одинаковы ! буквами.

Построения 1фшжоднм в такой последовательности

Сначала откладываем значения постоянной составляющей потока Фа и строим кривую Фж81пО)/-=/(©(}.

Затем пршэвольно задаемся различными мсяжнтамя вршенн, например равными to/ = 0; п/2; я; Зп/2; 2л, и для каждого значения с пшощью кривой Ф=f{m) находим соотвегсгвунадге значения Ш