техники и изучения свойств нелинейных цатеи последние будут находить приметеине-для выполнения и других функций.

э перечисленных в данном параграфе типов преобразований (преоб-тоянного тока в перенотный и обратное преобразование, модуляция

н демодуляция, усиленве тока, напряжения, мощности) осуществлиют с помощью нелинейных устройств, и в этом смысле они являются нелинейными преобразователями. Однако прн определенных условиях в относительно небольшом диапазоне взмененнй входной величины эти преобразователи могут обладать почти линейной зависимостью амплитуды (денс1вуюп4его иЛи среднего значения) выходной величины от амплитуды (действующего или среднего значения) иходнои.

Вне этого днапвзова завнсимйсть выходной велнч1)ны от входной являегся в 1ой или иной степми (часто в очень значительной) нелинной.

Для многих других типов преобразователей (Например, логарифмических и степенных) зависимость выходной величины от иходной ве может быть линейной, так как это противоречило бы самому назначению и самому принципу работы преобразователей этого типа.

Если же зависимость ныходаой величины от входной может быть линейной, нли близкой к линейной, ю вбслыьннстве случаев стремятся выбрать режим работы преобразователя таким образом, чтсбы работа его проходила именно на линейном участке. Так поступают, в часпюста, при использования электронных, полупроводниковых и магнитных усилителей тока, напряжении.

§ 15.10. Некоторые физические

е в нелиней-

ных цепях. В электрических цепях переменного тока, содержащих нелинейные индуктивности и линейные емкости или нелинейные емкости и линейные индуктивности, а также нелинейные индуктивности и нелинейные емкости, при о1федеяенных условиях (далеаю ие всегда!) возникают физические явления, которые невозможны в лгненных цепях *. Таких явлений довольно много. Ограничимся кратким рассмотревиш только некотсфых, наиболее важных вз них:

1. Возникншение иитеношных колебаний в цепн нэ высшей гармонике при отсутствии этой гармонжи во входном напряжении.

В линейных цепях Бозникнсжение интенсивных колебаний на ысщей гармонике может быть только при наличии этой гармонтжи бо входном нвпряжении.

2. Возникновагае субгармонических колебаний.

Под субгармоникой понимаЬэт гаруонику, частота котсзой в целое число раз меньше частоты источника э. д. с. Субгармонические колебания представляют собой колебания на какой-либо из субгармонж. Чаще всего они наблюдаются на частотах ю/3; ю/2; со и т. д. (ш -частота источвжа э. д. с.)- см. § 15.53.

3. Возникновение колебаний в цепи на гармонике с частотой ты/п, где m н п - целые числа.

4. Заввагаюсть характера установившегося режима в нелинейной цепн переменнрго тока от предшествовавшего этому режиму состояния,

, цепи и начальной фазы псточинка э. д. е., от которого питается цепь. Это явление может наблюдаться в нелинейных электричких цепях в зоне существования триггерного эффекта, о котором было упомянуто в § 15.9. Суть явления состоит в том, что при подключении нелиней-

* Имеются в виду обычные* линейные пепи. шфаыетры которых ве являются функцией времени. О линейных цепях с непосюшншш во премени параметрами

ной резонаиск* цепи к источнику э. д. с. в ней можег возникнуть один из двух возможных режимов. Какой вз режимов возникнет, зависит от начальной фазы генератора и состояния цепи, предшество-вавшега включению(см. § 15.591. 5. Вошикновение автомодуляции.

Авпюмодуляция представляет собой процесс перирдитесксято или почти периодического изменения амплитуд токов и напряжений в нелинейных электрических цепях без воздействия на них внешнего моду-.чирующего фактора, т. е. без возщокггвня на них низкочастотного сигнала (см. § 15.56).

Перетислеяные физические явления имеют место в резонансных цепях только в шределенных для каждой цепи диапазонах параметров, котсфые, как правило, оказывиогся такими, что практически эти явления наблкщакпся сравнительно редко. Кроме того, исгледшанне условий возннкновети этих явлений часто связано с весьма гройозд-кими матшатаческими выкладками, поэтому в курсе с достаточной полнотой отразить все эти явления трудно. Подробнее можко ознакомиться с этими явлениями по [21] и [22].

§ 15.11, Разделение нелинейных сопротивлений по степени сим-кетрин характеристик относительно осей координат. Кроме деления па а.ктивные, индуктивные и емкостные, управляемые и неуправляемые (а активных -еще на безынерционные и инерционные) нелинейные сопротивления можно классф1цировать еще по одному признаку - по степени симметрии характеристик для мгновенных значений относительно осей координат.

Пусть X и i/-величины, характеризующие режим работы нелинейного сопротивления. Условимся jc (означать величаку, откладываемую по оси ординат декартовой системы, а /-величину, отклздывашую по оси абсцисс-

Харакгеристики, для котсых выполняется условие-i/(-Jt)=i/(jr), принято называть симметричными: характеристики, ие удовлегвфяю-щне этому условию,-кешАшетричйшш.

Симметричными характеристиками обладают нелинейные индуктивностии емкости, а из активных сопротивлашй - тиритовые сопротивлення, элвстрическая дуга с однородными электродами и некоторые другие-типы сопротивлений.

Однако основные типы нелинейных активных сшротивлений - электронная лампа, транзистор и тиристор - имеют несимметричные характеристики.

В ближайщих 13 параграфах рассматриваютй! основные особошосга работы нелинейных сшротивлашй с симметричными характеристиками.

Основные особенности работы нелинейных сопротивлений с несимметричными характеристиками -электронной лампы и транзистора - излагаются в § 15.27-15.43.

§ 15.12. Ап!

I характеристик нелинейных сопротивле-

ний. Для йотедения математического анализа непннйй1ых цепейлере-ыенного тока и изучения их общих свойств целесообразно выразить

аналитатески зависимость между мгнотенными значениями н i дл нелинейного активного (отротивления, зависимость между В и И nf№ нелинейны! индуктивности, зависимость д и и для нелинейной шкости. Приближенное аналитическое описание характеристик нелинейных сопротивлений принято называть annpoKcuMat характеристик.

§ I5.IS. Аппроксима1(ия сим

с характеристик для мгн

венных значений гиперболическим синус<ш. При исследсяании свойстч элопрических непей явлениш гнстереш:в, как правило, можно небречь. Лишь при исследсеании цепей, в основе действия которые; лежит это явление {например, работы запоминающих магнитных устройсг! с прямоугольной петлей гистерезиса), гистдзезис необходимо учиты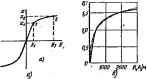

На рис. I5.II,a изображена типичная симметричная характе] стика y=fix).

Для нелинейнс* ицдукпшносги рель х играет мпкженное значе ние нцдукции В; роль мпкжашое значение напряжеяност. поля И. Для нелинейной емкости роль у играет напряжешю и. роль X-зард д. Для нелн№йных активных сопротивлшии (naiH мер, тиритовых согфотивлений) роль х играет наприжение, роль у ток.

Существует большое количество различных аналитических выражс ВИЙ, в той или иной мере пригодных для аналигичеоюго описани. характсрисяж нелинейных сшротивлений [21]. При выборе наиболп подходящего аналигаческого выражения для функции y=f(x) исхо дят не только нз того, что кривая, ошгсываемая аналитическим выра жением, должна достаточно близко всеми своими точками распслэ житься к опытным путем полученной кривой в предполагаемо! диапазоне пшшиенпй рабочей точки на ней, но учитывают i те-возмшщостя, которые выбранное аналитическое выражение да-при анализе свойств электрических цепей. В дальнейшем для аналт тичежого описания характеристик симметричных сопротивлен* но типу рис, 15,П, а будем попьз<жаться гиперболическим сину<и у=а9Ьрх. (15J

В этом выражении а и р -чпслотые коэфвдешы; а измеряется в тех единицах, что w у; р-в единицах, обратных единицам измерения x, так что произведение есть величина безразмерная. Для определения двух неизвестных коэффициентов и и р следует на полученной опытным iiyrcM .зависимости y=f{x)b предполагаемом рабочем диапазоне провзвольно выбрать две наиболее характерные точки, через KOTquJe должна пройти аналитическая кривая, подставить координаты этих точек в уравнение (15.1) и затем решить систему из двух уравноши с двумя неизвестными.

Пусть координаты этих точек Ху н у, х (рис. 15.11, а). Тогда

yi = aslipx,; y=asbfiX2.

Отношение

fe/ifi = shp,/shp*j. (15.2)

Трансцвдднтюе уравнение (15.2) служит для определения коэффициента р. После этого определяется коэффициогг

ayshfix. (15.3)

Пример 147. Кривая намагничиввиия трзисфорыаториой стали Э41 изображена иа рнс. 15.11, б. Найти коэффициенты айв.

Решение. Выбираемое точки на привой: й(=200 А/м; В, = 1.1 Т; = 2400 А/м; Ва= 1,532 Т-

По уравнению (15.2) имеем sh (l,532fS)/sh (l,lfl)=

---------- - производим подсчета:

Р... 6 52 47

рВа ... 8,2 8 7

pBi ... 6.6 5,74 S,03

shpSaMpBi- 13.5 9,58 7.25

12. Задаемся произвольными 3.92 3,26

3,59 4.1

, , подсчетов строим кривую sh PBi/sh рв,=/(Р) и по ней

находим р=5,75 Т . Далее определяем

аНфЬ pBa=2400/sh 8.82 1200/1690==0.71. Пунктирная крнаая рис. 15.11, б построена по уравнению =0.71 sh (5,75 В).

§ 15.14. Понятие о функциях Бесселя. Прн

используют функции Бесселя, которые

(15.4)

Фулкция Бесееля ньфажаются степенными рядами и для них составлены таблицы. Функцию Бесселя от аргумента * обозначают/ (л;), где р-порядок функции Бесселя. Общее выражение для Jp(x) в виде степенного рада имеет вид , .(хтР (х/2)Р . (х/2)Р (х/2)Р ,

Для гл. 15 наибольший интерес представляк мнимого аргумента. Для нх получения в общее

функции Бесселя i ыраженве (15.5) i

дует подставить /х, гдв 1. Обратим внимание на то, что в табл. 15.1

дана фуякпяя -/J((/jO вместо /,(/ ), функвдя ,(/ ) вместо/s(/Jt)-Сделано это потому, что без донолнительвого множителя / или -/этн функции, как правило, не используются.

Таблица 15.1

нкцня Бесселя нулевого ворядка: Jo(0) -рив

Пря x=f> не равна нулю только = 1. По двнным табл. 15.1 на рис. Из таблицы н рис. 15.12 видно, что с ростом х анач Чем выше порядок функции Бесселя, тем меньше

§ 15.15- Разложение гипербопичесиик синуса н косинуса от пжсщическог аргумента в ряды Фзье. Если аргумент к изменяется вапрпнер

и фувкняя sh(xejnw и гЪ1х етШ). Тая как периодические фу цнн можно предстввнть рядами Фурье, то ра лочим в рцд Фурье эти функции. С это* це лью в (15.5) вместо к подставим хйпт/. уч тем мзвестные нв тригонометрии формулы:

dn o=0.5-0,5cos2a: (IB.l

8ln>a=~ 0.23 cjn 3a--0.75 sin a; (15-

rin*a=O.375-0.5cos2a-b0.125cos4a. (15Л

al, cos2iu 0 выделим n

стоянную сосгавлакщую. В результате групп, ровки оказывается, что козфжциентами щ. трягонометрическнх функциях являются рад которыми иаобрансаются функции Бесселн различных порцдков от чисто mhpiw аргумекга /хщ- Окоичателько получим:

ch(x dn 0-y (,*J+2J,(/>COe2u,r+2;.Ox Jcos4(o i-b... (15J

Ряд для Ixwitut) соспжт только из нечетных гармоник и не яыеет гтопояниов составляющей. Рад для сЬ (х anal) имеет постоянную составляющую ,1 четные гармоники.

Пример 148. Разложить в ряде Фурье sh(4dn(iiQ и ch(4 n Q. Решение. Значения функщ*й Бесселя берем нз таблицы: (/4)=9,76; /Л(/4)=3.34; Jj(/4)=1.416: -/(/4)0.505: У (/4)=11.3: Ja{;4)=-6.42. В соответствии с (15.9) я (15.10) получим:

sit (4ипи0=2.9,76ЯПи(-2-3.34 sinЗм(2.0.505ип5 (!-...{ Ь (4 йп = 11.3-2 6,42 cos 2(а( 2 -1,416 cos 4w( . ..

§ 15.16. Рам

инуса с

функции у с <! 1рмуле аргументом гиперболнческ(

к .в ряд Фурье. Из§ 15-13

x формулой (Hi.l)- В этой 5 ве к, как было в §I5-I4.

а произведение р*. <В соответствии с этим для разложжия-sh (Р): sin <iiQ и с\1 (р): sin иО в (15.9) и (15.10) следует вененить х на {к.

- Если :=jrfl-f Jfei 8ino)(, где jtj-постоянная составляющая, амплитуда

снусондальной составляют., то

у=а sh (Рло pjcm йп ы1) =се sh рл, ch (Р sin юД +а, ch рд- sh фх sin nil).

Следовательно.

j=a sh рлгв[J.-J-2J, Wx )cos 2ш/-J-SJ, (/p >cos4ш(-J-... +

-J-achрлгв (2 H fJ, (/P m)) ein (-2,V, (/p > sin (15 11)

Из (15.11) следует! чю постоянная составляющая функции у

tfe=ashpVe(/P m)-Первая гармоника функции у

вторая гармоника третья гармоника

(15-12)

(15.13) (15. М (15.15)

II т. д. ,

Пример И9. Разложить в ряде Фурье функцию ff/ra=sh (2Ч-4 sin сйЛ. Решение. По табл. 11.1 находим sh 2=3.63; di?=3.7. Значения функций

Ссселя берем ив табл. 15.1. В соогеетствин с (15.11) имеем

y/a=sh(2+4 81пЫ)=3.63 (11.3-1244ces2tt,/-l-232cos4ш(-...)--3,76 (19.52 Йп W/-6j674 cjn Ш+1,01 sin 5ш/-...). Таким обрезом, ро/и=41.1; йт/а~73.4; !/Wa=.7-

й=2а ch pjTa Н Их (/P sin ft=2а sh pjr, [Л tfp-v ,>l cos 2 (; Sr,=2a ch pjr.[- ,

1ЫХ нелинейных ci

ЮЙ характеристи!

инея x, изменяется во bjmchh о закону хха+хщп&1, гон определяюгоей его состояние величины (величины Д маяа

раСотае например пели

сделать с-педуюогне

составляющая функция аавнснт ве только от во и

выводы,

I. Постоян] .

w * . Это слеетет из формулы (15.12).

S. В кривой у=ц[Ы) ноянляются лО. Фаза четных гармоних зависит от (от знака xaj.