-Для определения Я н на рис. 14.18,вследуетнанестипрям 1 построенную по (14.12). В точке пересечения прямой с кривой р магничивания удовлетворяются обе связи между Bj и котсф< должно быть подчинено решение.

Приведенный расчет даст достаточно точный результат, если зазор в №л мал по сравнению с длиной i. Если это условве не вынолнеио. то значителья часть магнитны силовык линий замыкается, как показано пунктиром на рис. H.IjS, В этом случае поток, индукция и напряженность вдоль сердечнвка изменяюто

Пример 144. Найти В До, и Яе, если постоянный (рис. 14,18,6) имеет / = 5см; 6=1 см. Кривая размагничивани изображена на рнс. 14.18,с.

Решение. Еслн пренебречь боковым распором магнитных линий в зазоре, то 8в = 8е. При этш размагничивающий фжг =263-\0\ На рис. 14.18, в проводим прямую ( по уравнению Я =-263-Ю-Д,

Точка а ее пересечения с кривой размагничивания дает Д = 0,3 Такая же индукция будет в воздушном зазоре. Напряженность п& в теле магнита- Яс=-8000 А/ы. Напряженность поля в воздуиша зазоре Яе-0,8-10 -0.3 = 24-10*(А/м).

§ 14.22. Прямая и коэ<

ант возврата. Частично залолш

зазор б на длине фис. 14.18,6) куском магнитномягкого маи риала. Под действием поля постоянного магнита внесенный ку-- намагнитится и поток в теле магнита возрастет.

Ввиду наличия гистерезисе магнитное состояние постоянного инта будет изменяться не по участку аЬ фис. 14.18, кривой магничивания. а по нижней ветви adc частного шасла.

Для упрощения расчетов принято заменять частный цикл прям линией, соединяющей его вершины. Эту прямую линию назыви прямой еозеретт.

Тангенс угла наклона прямой возврата к оси абсцисс иазыва -коэффициентом возврата. Его числовые значения для различны магнитнотвфдых материалов даются в руководствах по постояним магнитам.

Сбозначим длину сставшегсся воздушного зазора (рис. 14.18, 6 = 6 - / и на основании %акона полного тока запишш

Напряжен.чость поля в магнитномягком материале Я е многз меньше напряженности поля в магнитнотвердом материале и в воз душном зазоре при одном и том же значении магнитной индук1даи поэтому слагаемым Яи.Л.с пренебрегаем по сравнению с остальными Гн этом

Яе1л/.,=0,8.10*Д,(П. (12-

Магнитное состояние постоянного магнита определяется пече- кит прямой возврата с прямой, построенной по (14.(2).

Пример 145. Воздушный зазор магнита примера 144 уменьшен сивое. Найти индукцию в н&л.

Решение. Находим W=I31,5-IO*. Прямая OA (рис. 14.8,в> гересекается с прямой возврата в точке d. Поэтому Дс = 0,42Т. Такая же индующя будет и в воздушном зазоре, так как Sc = S.

Следовательно, уменыпение зазора со значения б до 6 привело к увеличению магнитной индукции в нем с 0,3 до 0,42 Т.

Если же величину зазса 6 получить не путем его уменьшения со значения Ё до б, как в предыдущем примере, а путем выемки из намагниченного сердечника куска длине* f>i, то магнитное состояние магнита определится пересечением луча OA с кривой размагничивания baf в точке е. В этом случае Дс = Дв=0,48 Т, т. е. возрастет по сравнению с магнитной индукцией примера 145 на х

> 100 = 20%.

Таким сбразом, магнитный поток в постоянном магните Зависит не только от величины воздушного зазора, но и от предыстории уста-Р:Овления этого зазора.

§ 14.23. Магнитное сопротивление и магнитная проводимость участка магнитной цепи. Закон Ома для магнитной цепи. По определению, падение магнитного напряжения U-Hl, но

Я = Д/(р,р)=Ф/(р ц5),

где Ф -потек; S-поперечное сечение участка. Следовательно,

-15=*- 04.14)

откуда

;г. = №оц5): (14.15)

Уравна1ие (14.14) называют законом Ома для магнитнвй цепи. Это уравнение устанавлтшает связь между ticueM магнитного напряжения V и потоком Ф; jR называют магнитным сопрааивяеныем участка магнатной цепи. Обратную величину магнитного Сопротивления называет магнитной проводимостью:

G =l/i; -PoS . (14.16)

Из предыдущего известно, что вебер-акшерная характеристика участка магштюй цепи в общем случае нелинейна. Следовательно, в общем случае и G, являются функциями магнитного потока (непостоянными величинами). Поэтому практически понятиями и 0, прн расчетах пользуются лишь в тех случаях, когда магнитная цепь в целом Или ее участок, для которых определяются и G , не насыщены. Чаще всего это бывает, когда в магнитной- цепи имеется достаточно большой воздушный зазор, спрямляющий вебер-амп)ную хгч)актери- стику мапишкй ци1и в целсяа или ее участка.

Магнитное сшротивление .участка цепи можно сопоставить i статическим сотротявлением нелинейного сотротивлення (см. § 13.1. н так же, как последнее, можно использс ать при качественно рассмотретни различных вопросов, например вопроса об иэлен-потоков двух параллельных ветвей при изменении потока в нера вленной части магнитной цепи (как в § 13.2 по отношшию к электри чесжой цепн).

Пример 146. Найти R воздушного зазора постоянного магнит и магнитный поток, если 6 = 0,5 см. площаць поперечного сеченн воздушного зазора S=1.5cм [/ = 1920 А,

Решение.

~ 1.256.10(Г/мМ-1-10(н -

= 0,256-10 (Г-);

0 = UJR= 1920/0,256.10 -7230-10- (Вб).

§ 14.24. Пояснения

площадку as, создает т равен ппошОА as. а

i формуле fi=it (Й-Ь/). Контур нтА1=.-4Г

а правилом правого винта.

:.(4S(phc. 14.19, о). Вектор AS : направление aS

ВиВерхштый дал С люшшкй ппвтестю Ь , чисшмд реЬввв 3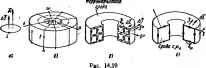

)гннтный кольцеаоВ сердечник (рис. 14.19,6) в

виткое т. по которой проходат ток /. Каждая единица объема ферромагни а обладает некоторым вектором намагниченносга 7, что при расчете м

феррсшагнтнон материале контуров ---------------двчника на рнс. 14.19,

[рниодящегос: 1НИЧНЫЙ вектор

единицу длины сердечника i , . - .

совпадающий по направлению с направлением обозначим V. Молекуля], ток ёнип охватывает площадку as. Положительное направление вектора А? -ass связано с положительным направлением этого тока правилом npi винта. Через S обозаач£Н единичный вектор по на1фавлению aS,

По определению, иамагниченвость 7 представляет собой магннтныймсяяе! единицы объема вацества. Средаюю по объему намагниченность вещества J мож определить лутем деления ыагнитнсго момента контура с током %Jut, oxaai рающим площадку as, и

обьен &V=&l&S:

О Объему иагшгншешикть 7 численно равна средней а и направлена по S°.

руют друг друга. ]

(олекулярные i

между сосед-напраелены встречно и взаимно компенсн-1ми остаются только тока по периферийному

контуру (рис. 14.19, а).

1*так, наличие областей самопроижсдьисЛ намагниченности в ферромагнитном теле при расчете можно эквивелентировать протеканием ло поверхности этого тела, считая его неферроыагнвтным. Поверхностного тока с линейной плотностьюби, причем по модулю

Запишем 1фавнение по закону полного тока для контура, показанного пунктиром на рис- 14.19, б. При этом учтем, что после введения поверхностного тока сердечник станет неферромагнитным в вудет намагничиваться не только током /. протекающим по обмотке с числом витков w, во в поверхностным током с линейной лотностъю в .

На длине dl новерхностныЙ ток равен S-Jdl. tut длине Hceio сердечника говерхностный ток равен ф Jdl. Таким образом.

, 7 Л=/ш.

Величину ~.-J обозначают Я и

н индукции В I

е аависит от магнитных свойств [ того, чтобы закон

J напряженность поля Н аемого тела Это и явилось основа-для любых сред записывать в виде

-.Iw.

10 высоте и по тол-туров ни рис. 14.19. в неоди-компенсируются

Если ферромагнитное тело намагничено щнне, то плотность молекулярных токов смеж лакова, а тока на смежных между соседними контурами участках неполвостью. Отоода следует, что перавномерпо намагниченное тело прн расчете можно заменить таким же в гешлетрнческом смысле нитным телом, по новерхности которого течет новерхностныЙ ток, пло рого изменяется во высоте тела, а во внутренних точках тела течет объемный ток. плотность которого также изменяется от точки к точке.

1. Дайте определения В. 7, Н. Ф. (ig, (ц, Ц. Д - Ki - - - 2. В чек отли

собой СезгистерезисноЙ кривы:

измеряются? !

связаны между iHofi, основной и 8. Что понимают пся частным и вре-

i циклами, остаточной нвдукдаей, коэрцитивной силой, магтатаомягкнми и магнитнотвердами материалами? 4. Дайте отредепение понятиям м. д. с , магнитная цепь , магннтопровод ; 5. Как определшъ направление м. д. с? в. С какой Целью обычно-стретятся выполнить магнитную цепь с возм< (но меньшим воздушным зазором? 7. Как выбирают направление магнитных потоков в ветвях? е. Сформулируйте первый н второй законы Кирхгофа для магнитных цепей. 9. Перечислите этапы расчета цепей методом двух узлов. № В чем отличие магнитного иалряжения от падения магнитного напряжения? II. Как зкспёрименталыю получить постоянный мэтнит? 12. Как рассчитывается магнитная цепь е постоянным Ьагннтом? 13. Могут ли £ н J$ в ферромагнитном матерязле быть яа1фавлены естречио? 14. Решите задачи 3.2; З.ГО; 3.13; 3.15; 3.19.

а пятнадцатая

Е ЦЕПИ ПЕРЕМЕННОГО ТОКА

§ 15.1. Подаазделение нелинейных сопротивлений на три основные группы. Нелинейными электрическими цепями переменного пит называют электрические цепи пЧ)еменнаго тока, в состав которых входит одно или несколько нелинейных сопротивлений.

Как известно из ч. I учебника, прохождению переменного тока оказывают сопротивление не только активные сопротивлшия, i индуктивности и шкости. В соответствии с этим нелниейные сопро-ТИВЛМ1ИЯ для переменного тока можно подразделить на три гругшы: 1) активные, 2) кндукттштше н 3) елкостные. Каждую из этих групп можно подразделить на управляемые и неуправляемые.

Управляемые нелинейные сопротивления обычно имеют один или несколько управляющих электродов (зажимов) или управляющих обмоток, включашых в управляющую цепь (цепи), воздействуя на ток или напряжение которых можно управлять величиной сопротивления в главной цепи. При отсутствии специальных управляющих апйсгродрв или обмоток управляющий ток или напряжение могут воздействотать на нелинашое сопротивление через электроды или о&лотки главной цепи.

§ 15.2. Общая характсжстика нелинейных активных сопрорвле-НИИ. Ширсдаое расгфостранение в качестве управляемых нелинейных активных сопротивлший получили трех-(и более) электродные лампы, транз1яггсры и тиристоры. Свойства, принцип работы, характеристики и применение их рассмотрены в § 15.27-15.43.

Неуправляемыми нелинейными активными сифогавлениями являются электрическая дуга, германиевые и кремниевые выпрямители, тирито-вые сопротивления, термисторы, бареттеры, лампы накаливания и др. Их основные свойства и вольт-амперные характеристики обсужда в гл. 13.

Нелинейные активные сопротивления можно классифицировать также по степени влияния температуры нагрева сопротивления, обусловленной протекающим по ооготивлошю токстл, на фему вольт-амперной характеристики.

Так как тепловые процессы (процессы нагрева и остывания) являются процессами инерционными, то сопротивления, нелинейность в. а. х. которых в основном обусловлена ииленшиш тшпфатуры в результате нагрева протекающим через сопротивления током, .принято называть инерционными.

Согч50т влй1ия, нелинейность в. а. X. котсрых обусловлена иными (не тепловыми) процессами, принято называть безынционными почти безынерцвсяшыми.

К группе инерционных сопротивлений относятся электрические лампы накаливания, термистор, бареттеры; к группе безыне5)1даонных или почта безынерционных аяхэтнвленнй-элжгронные ламны пояупро-водниксшые диоды и транжтсы.

Если

периода переменного практически

и значением переменного т

и нагрева янерционного сопротивления много больше о величина сопротивления sa период переменного тока к она определяется ве ыгновевным, а действую-, Если к нелинейному инционкому сопротив-о подвести синусоядальное {апряжение (прн условии, что постоянная времени нагрева сопротивлення значительно больше периода синусоидального иаприжения), то ток через него будет практически синусоидальным.

Можно сказать, что яперциовные нелинейные сопротивления занимают прсвк-

...... * и сопротивлениями, К пели-

пение их является функцией то в установившемся режиме

работы их сопротивления для различных моментов времени внутри периода воздействующей на схему э.д.с. остаются практически -неизменными.

§ 15.3. Общая характеристика нелиней- - , ,

ныx индуктивных сопротивлекий. Под не- -Г линйными индуктивными сопротивлениями,

или нелинейными индуктивностями, пони- Рис. 15.1

мают индуктишые катушки с обмотками,

намотанными на замкнутые сердечнжи из ферромагнитого материала, для которых зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейна. Индуктивное сопротивление таких катушек, оказываемое прохождшню першетнсах) тока, непостоянно; оно завистгг от величины пфсмеяного тока.

Индуктивную катушку со стальным сердечником называют иногда дросселш со стальным сердечником.

feлинeйныe индуктивности подраздаляют на управляемые и неуправляемые, но деление иа безынерционные и инерционные на иих не распространяется, так как их нелинейность обусловлена свойствами ффромагнитного материала, а не Тепловым эффектом.

На электрических схемах нелннетную индуктивность изображанл либо в виде замкнутого сердечника с о&откой, как на рис. 15.1, а, либо в соответствии с рис. 15.1, б.

Сфдечники нелинейных ивдукгавносген при относительно низких частотах делают обычно двух типов: пакетные и спиральные.

Пакетные сердечники состоят из тонких пластав феррсыагнитногх) материала кольцевой, 11- нлн Ш-образной фермы.

Спиральные сердечники изпжжлнют из тонкой ферромагаитной ленты, по форме в виде туго навитой часовой пружины.

Пластины, пакетного и отдельные витки спирального сердечников изолируют друг от друга эмалевым лаком, жидким стеклом нлн каким-либо иным изолирующим составом н запекают. Изоляция необходима для уменыншия потерь энергии в сердечнике от вихревых токов (см. § 15.4).

Цзи высоких, частотах резко порастают потери в листовых сердечниках, поэтому сердечники, предназначенные для работы на высоких частотах, выполняют обычно из феррита.

§ 15.4. Потери в сердечниках нелинейных индуктивностей, обусловленные вихревыми токами. Если по индуктивной катушке со стальным сердечником проходит переадшый ток, то в сердечнике возникаег