болыииы. Если в мзгнятную цть входит ферромагйитный-1 ., то щлок в магнитной иепи при одной и той же м. X с. и-одиишо reoMeipmt цели <жаз1**.-г- И во много раз больше, чем случае отсутсгайя фсфс*. нитиого матиала.

Првмер 139. Возьми) т одинаковых в геометричеоов отасвиении кольцевых сердечника (рнс. 14.8).. Пусть ра диус их средние магнитной линии R = 10 см и поперечное сечезгае 5 = 2 см*. Один сердечник неффромагнитный, например деревяншлй, а дфу-. той - ферреыагнитный (кри* вая намагничивания рис. 14.9). Намотаем йа каждый кольцевой сдздечййк обмотку с числом ьитгай Ег-200 и -прсяу-стим по ним о.!ша1Ф№Й тЩ 1, например в 1 А. Опрецё лить потоки в сч)Дечни1й1х. Решение. По заксйу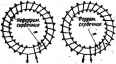

Рис. 14.9

дечниках и не зависит от ма-териала;

Я/ку(2яК)1-200/(2я.О,1) = 318 А/м.

Магнитный поток в неферрокагнитнс ! сфдечнике

Ф Ф = BS =ро}1Я5 = 1,256.10-* 318 - 2 10-* =8 - Ю * Вб.

По кривой намагничивания рис. 14.9 иажщнм. что при Я = 318 Рфл В* 1,02 Т.

Магнитный поток в ферромагнитном сздетнике

Фф = 65=1,02-10-*-2 = 20.4-10- Вб.

Таким образом, поток в фромагнитном сердечнике в 20,4-10*/8= = 2550 раз больше, ч&л в неферромагнипюм.

Ферромагнитные материалы ввожг в магнитную цепь также с целм сосредотоадння магнитного поля в заданной о(5ластн пространства придания &*у определишой ксффптрацин.

§ 14.11. Падение магнитного i

. Падением .

; между точками с и Ь магнитной цепи называют л1

ный интеграл от напряженности магнитного поля между этими точками:

1/ , = $ЯЛ. (14.6)

Если на эшя участке Я постояни* и совпадает по направлению с элементом njrrn dl, то HdlHdlcosO и Я можно вывести из-под знака ннтефала. Тогда

l}uabti\dl = HU,

(14.6а)

где / 6 -длина пути между точками о и &,

Падение магнитного нап>яжения измеряют в амперах (А).

В .том случае, когда участок магнитной цепи между точками о и 6 может быть подразденет на п отдельных частей так, что для каждой части Я = Я = соп51, то

§ 14.12. Вебер-амперные

(14.7)

iHCTHKH. Под вебер-амперной (максвелл-амперной) характеристикой (в, а. х.) * понимают зависимость потока Ф по какому-либо участку магнитной цепи от падения магнитного напряжения на этом участке: Ф=/(1/.

Она играет такую же важную роль при расчетах и исследовании магнитных цетей, как и в. а. х. нелинейных сопротивлений при расчетах и нсследжанни элаприческнх цепей с нелинейными сопротивлениями (см. гл.. 13).

В. а. x. при расчетах магнитных цепей в готовом виде ие задаются. Перед расчетом ях нужно построить с помощью кривых намагничивания ферромагнитных материалов, входя-щих в магнитную цепь. , i, S

% 14.13. Построение вебамперных характеристик. На рис, 14.10 изображен участок магнитной цепи, по которому проходит поток Ф. Пусть участки /i 4 сгнием 5 выполнены из ферромагнитного материала, кривая В = /(Я) для которого дэна, например,-на рис. 14,9, На участке длиной 6 магнитный поток проходит по воздуху.

Требуется построить в. а. х. ynacnia цепи между точками а Ь.

Пра построении допустим, что: 1) магнитный геоток вдоль всего участка от о до 6 постоянен (отсутствует рассеяние); сечение магнитного попжа в воздушном задоре такое же, как и на участкех и (отсутствует боковой распор силовых линий в зазоре, В действитель-

* в гд. 14 (в отлнчве от гл. 13) под в, а. х. понимается вебер-аыоерная иврактерисгнка.

ности оба допущения справедливы лишь в известной мере и больше воздушньй зазор, тем менее они справедливы.

Построение в, а, х, производим следующим образом. Задаемся рядом значений индукции В, например для эЯектротехнических сталей значениями 0; 0,5; 0,8; 1,0; 1,1; 1Д; 1,3; 1,4; 1,5 Т, и для казкдого значения В находим напряженности поля на всех участках (/j, /g и б).

На участках из ферромагнитного материала (участки 1 и /g) напряженность HiHz (так как Bi = Bs) находим по кривой намагничивания.

Для неферршагнитных участков участок 6)

Таким образом, для определешя Я (А/м) в воздухе следует умножить ицдукцию, выраженную в тёслах, на коэффициент 0,8-10*,

Для каждого значения В определим поток Ф = В5 и навдем

По результатам подсчетов строим кривую Ф = /(1в).

Примф 140. Построить в. а. х. для участка цепи рис, 14.10 прн е=0; 0,005; 0,05 см; =10 см; 1 = 5 см; 85 см\

Решение, Определим падение магнитного напряжения между точками а в b участка магнитной Рис 14 11 цепи рис. 14,10 при 6 = 0,005 см и

В = 0,5 Т.

Из кривей рис. 14.9 находим, что нцдукции В = 0,5 Т соответствует напряженность поля Я = 40 А/м. Таким образом, при В--0,5 Т lii = H = 4Q А/м.

По формуле 1/ сь = ЯЛ+Яаа+Яве подсчитываем t/ o = 40-0,1+40- 0,05+0,8 - 0,5-10 - 5-10-* 26 А,

Значения иь при иных зазорах н индукциях находим аналогичным образом. Подсчеты сводим в табл. 14,1.

Таблица 14.(

По данным таблицы на рнс. 14.11 построены в, а. х. при трех значениях б. Из построений видно, что если участсж, для -которого сфож в. а, X., не имеет воздушного шлючеяня, то в. а. х, круто понимается вверх. При наличии воздушного включения в. а, х. спрямляется и вдет более полого.

§ 14.14. Законы Кирхгофа для магнитных цепей. При расчетах магншнУх цепей, как и электрических, используют первый и второй законы Правила) Кирхгофа,

Первый закон Кирхгофа: алгебраическая сумма магнитных потоков е любом узле магнитной цепи равна нулю:

2Ф = 0. (14.8)

Первый закон Кирхгофа для магнитных цепей следует из принципа непрерывности магаиикхх) потока, известного из курса физики (см, также § 21,8).

Второй закон Кирхгофа: алгебраическая сумма печений магнитило напряжения вдоль любого замкнутого контура равна алгебрашеской сумме м. д. с. вдоль того же кттура:

(14.9)

Второй закон Кирхгофа для магнитных цетей по сути дела есть иная форма записи закона полного тока.

Перед тем как для мапошгой цепи записать уравнения по законам Кирхгофа, следует произвольно выбрать положительные направления потоков в ветвях магнишой цепи и положительные направления обхода контуров.

Если направление мапштного потока на некотором участке совпадает с направлашил обхода, то падейне магнитного напряжения этого участка входит в сумму V со знаком плюс, если встречно ему, то со знаком минус.

Аналогично, если м. д. с. совпадает с направлошем обхода, она входит в 2/и со знаком плюс, в противном случае-со знаком минус.

В качестве примера составим уравнения по законам Кирхгофа для разветвлашой магнитной цепи, изображенной на рнс. 14,12,

Левую ветвь назовем nqjBOH, и все относящиеся к ней величины будут с индексом 1 (поток Ф напряженность поля Ии длина пути в стали /i, длина воздушного зазора 6i, м. д, с, /щ).

Среднюю ветвь назовем второй, и все относящиеся к ней величины будут соответственно с индексом 2 (поток Фа, напряженность поля Яе, длина пути в стали 1, длина воздушного зазора 6, м. д, с. /вШ.

Все величины, относящиеся к правой ветви, имеют индекс 3 о-ток Фз, длина пути иа вертикальней* участке суммарная длина пути на двух горизонтальных участках Га).

ГЪнзвОйьно выб)ем направление цотоков в ветвях. Положим, что все потоки (Ф, Фа, Фд) направлены вверх (к узлу а). Число

уравнений, которые следует состиить по законам Кархгофа, . быть равно числу ветвей цепи (в рассматриваемом случае нужно составить три уравнения).

По первому закону Кирхгофа необходимо составить столько уравнений, сколько в цепи узлов без единицы (см. § 1,8),-

В цепи рис. 14.12 даа узла; следжателыю, по первому закону

Кирхгофа составим одно уравнение:

Ф.+Фа+Фа=0- (а) По второму закону Ккрх-гофа следует составить число уравнений, равное числу ветвей, за вычетсяа числа уравнений, составленных по первому закону Кирхгофа, В paccMaTpHBacNTOM примере по второму закону Кирхгофа составим 3-1=2 уравнения.

Первое из этих уравнений составим для контура. Рис. 14,12 образованного первой и втот

рой ветвями, второе -для контура, образованного первой и третьей ветвями (для периферийного контура).

Перед составлений уравнений по второму закону Кирхгофа необходимо выбратьположительное направление обхода коптуров. Будем обходить контуры по часовсй стрелке.

Уравнение для контура, образованного первсй и второй ветвями.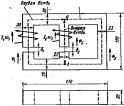

где Яс1 и Яца-напряженности поля соответственно в воздушных зазорах bi и

В лщ/vo часть уравнения вошли слагаемые Я,/1 и Яб, со знаком плюс, так как на пфвом участке поток Ф, направлен согласно с обходом контура; слагаемые Я/а и Ябз-со знаком минус, так как поток Фз направлен встречно обходу контура,

В правую часть уравнения м. д. с. Iw вошла со знаком плюс, так. как она направлена согласно с обходом контура, а м. д. с. /gtWa-со знаком минус, так как она направлена встречно обходу

им уравнение для периферийного контура, образованного первой и третьей ветвями:

<в)

Срвмрсгао решать три уравнения {(а), (б), (в)] с тршя ии1заес JMH (Ф1, Фа, Фд) ие будем, так как в § 14Л8 дается рещение рас-.-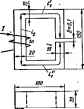

Рвс. 14.13 1 ферромагнитного мате-

алатриваедой задачи более совершенным методом, чем метод на основе законов Кирхгофа, -методом двух узлов.

§ 14.15. Применение к магнитным цепям всех методов, исполь- зуемых для расчета электрических цепей с НС. В гл. 13 подробно сбсуждались различные пришы расчета электрических цепей с НС. Все эти методы полностью применимы и к расчету магнитных цепей, так как и магнитные и электрические цепи подчиняются одним и тйл же законам-законам Ккрхгофа.

Аналогом тока в электрическсй ценя является поток в магнитной цепи, аналогом э, д. с -м, д, с. Аналогом волЬт-ампе[ юй характеристики нелинейного сопротивления - вебер-ампер-ная характеристика участка магнитной цепи,

§ 14.16. Определение м. д. с неразветвленной магнитной цепи по заданному потоку. Заданы конфигурация и гесниетрические размеры магнитной цепи, кривая (кривые) намагни . .. риала и магнитный поток или нвдукция в каком-либо сечении. Требуется найти м, д. с, ток или число витков намагничивающей обмотки.

Расчет прсеоднм в такой последсвательносгн:

1) разбиваем шгнитную цепь на участки постоянного сечения и определяем длины (м) и площади поперечного са!ения Sh (v?) участков (длины участков берем по средней .силовой линии);

2) исходя нз постоянства потока вдоль всей цепи, по заданному потоку и сечениям S* находим магнитные нвдукции на каждом участке:

3) по кривей намагничивания определяй) напряженности поля для ферромагнитных участков магнитной цепи; напряженность поля в воздушном зазоре

Яа/ =0-10 Вт; (14.10)

4) подсчитывав сумму падешш магшпяого напряжения вдоль всей магнитной цепи Hkli, и на основании закона полного тока праравг ннвэем эту сумму полному току 1ж

ХЯл1* = /и.-

Основным допущенийл при расчете является то, что магн1ггный поток вдоль всей магнитной цепи полагаш неизмогным. В деисген-телй1Ьс*и йебольшая часть потока всегда замыкается, минуя осжйнсй путь. Например, для марнитной цепи рис. 14.6 поток, выйдя из левого