Пример 13. Найти токи в ветвях схемы рис. 1.24 и сделать npi ерку по второму закону Кирхгофа. Дано: £;, = 10 В; £ = 6 В; £;, = 20 В; £;,=30 В; Ей 14 В; £ =10 В; Е =В В; К.= 12 В; ё;, = 7 В; К;,-1 Ом; %=2 Ом; К;, = 10 Ом;. ,-, 10 Ом; Ri=5 Ом; ? -2 Ом; R =i Ом; Ru-i Ом;

КЬ = 4 Ом; R =2 Ом. Источник тока. включенньЛ между узлами 3 и 2, дает ток lia, = 1.5 А.

Решение. Записываем систему уравненнй:

Ф1С11 + 9jGia+фзрхз = /ц; Подсчитываем проводимости:

Оя=0 =-(0,25 + 0.6)=-0,76 См.

При подсчете G. С33 и Gj, учтено, что проюдимость ветвн с яиком тока равна нулю (сопротивление источника тока равно нечносги).

Узловые токи:

, е;, Si 15 д.

/ =-3.6+3-7+4-1.5=-6 А. Система уравнений

2.4ф,-0.4<р,-0,6ф,= 16; -0,4(р,+1,4ф, - 0,75f,= -1 ,В; -0,5ч), - 0.75<1., +1,754)3=-5

имеет решение: 4>i=6 В; ip2 = 0,06 В; Фз=-1,07 В.

Заключтельный этап расчета состоит в подсчете токов по закону Ома. Перед определением токов в ветвях схемы следует эти той

обозначить и выбрать для них положительные папрааления: /;,£i-fc:ii2ri) = 4 А: /-=2-= М85 А;

= SLZ:±£k2,92A; / = *Ь4.55А н т. д.

Сделаем проверку решения по второму закону Кирхгофа для пе-рифернйного контура.

/йгебраическая сумма падений напряжений

4-1 + 1,185.5- 2,92-2 - 4,55.2-5 В.

Алгебраическая сумма э. д. с.

10-7-8

= -5 В.

Покажем, что основная формула (1.20) метода двух узлов получается как частный случай из формулы (1.22). Действительно, если одан узел схемы рис. 1.23, например узел Ь, заземлить, то остается найти только один потенциал ф = (/ва. Дггя получения формулы из следует положитк ч>1=Фо=4/аб; Фа=Ч>э=Ч>1 = ..-=0.

§ 1.22. Т1рес>фазованне звезды в треугольник и треугольника

в звезду. Соединение трех сопротивлений, имеющее ввд трехлучевой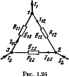

йвезды (рис. 1.25), называют i

шш звезда, а соеданение трех сопротивлений так, что они офазуют собой стороны треугольника (рис. 1.26).-соединением треугольник. В узлах I, 2, 3 {потенциалы их <Pi и Фа) и тргольник и звезда соединяются с остальной частью схемы (не показанной на ритжах).

Обозначим токи, подтекающие к узлам /, 2, 3, через 1, и /д. Очень часто при расчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо прюбразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одаоиммшых точек тре-Угощжика н звезды подтжающие к этим точкам токи одинаковы, то вся внешняя схема вне заметит произведенной замены. Выведем

формулы преобразований. С этой целью выразим токи /i, /а и /я в звезде и в треутольнике через разности потенциалов точек и соот ветствующие проводимости.

Для звезды

Л = (<Р1-фа)£1: /в-(ф!- Р!)£2: /1 = (ф!-1 Подставим (1.24) в (1.23) и найдем ф,:

Vigi++- Pi (gl +g2+g,)=0,

Далее введем (f в вы;

i (1.24) для тока

/.=(Ф,-Ф.)&=!Ь±2*й!й.

(1.23) (1.24)

(1.25) (1.26)

Для треугольника в соответствии с обозначениями на рис. 1.26 i = м - и - (fi - 4>i)gM - (Ъ - 4>i)gM = <Pi (gu+gis) -

-<PAa-<f£n- (1.27)

Так как ток /, в схеме рис. 1.25 должен равняться току 1 в схеме рис. 1.26 при любых значениях потенциалов ф (Рз, Рз, то коэффициент при (Рз в правой части (1.27) должен равняться коэффициенту при Фа в правой части (1.26), а коэффициент при фз в правой части (1.27) должен равняться коэффициенту при фз в правой части (1.26). Следовательно.

gi! = gig /(gi+g2+g.); (1.28)

gn = g.go/(g.+g.+g,). (1.29)

Аналогично,

go=g.S3/(gi+g8+gs). (1.30)

Формулы (1.28)-(1.30) дают возможность найти проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимосгей в числителе правой части соогветггвуют индексам у проводимости в левой части, в знаменателе-сумма цроводимостей лучей звезды.

Из уравнений (1.28)-(1.30) выразим сопротивления лучей звезды i 1/gi: l/ga и /?з= l/ga через сопротивления сторон треугольника:

Ru=i/gu; R ,-i/gn; R =i/g .

с этой целью зашпием дроби, обратные (1.28)-(1.30):

1,= .К ----=f. (I.3I)

ft к.

Здесь

R = m/Rj.

Подставив (1.31), (1.33) в (1.34) в (1.32), получим

(1.32) (1.33) (1.34)

Следовательно.

Подставим т в (1,33) и найдал

Аналогично,

(1.35)

(1.36) (1.37)

Структура формул J1.35)-(1.37) аналогична структуре ффмул {i.28)-(1.30).

Полезность преобразования треугольника в звезду можно пояснить, например, схемой рнс 1.27. На рис. 1.27, а изображена схема до преобразования, пунктиром обеден преобразуемый треуголь- ник. На рис 1.27,6 представлена та же схема после преобразования. Расчет токов производить для нее проще (например, методом двух узлов), чем расчет токов в схеме рис. 1.27, с.

В полезности преобразования звезды в треугольник можно j-eeflfffbCH на примере схемы рис.. 1.27, е, а. На рис. 1.27, в изображена схема до преобразования, пунктиром сведена пре-оазуемая в треугольник звезда. На рнс. 1.27, г представ- кис. лада схема после преобразова-

иия, которая свелась к последовательному и параллельному соединению сопротивлений *.

* в § 3.31 fpaccMOTpeH еще один вид преобразований - преобразование по-<ова1ельно.параллельного соединения в параллельное.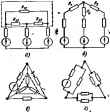

пример 14. Найтн значения сопротивлений R, R в схеме рис. 1.27, б, если сопротавления R, К,а. Rss в схеме рис. 1.27, а равны соотаетственно 2, 3, 5 Ом.

Решение. По формуле (1.36), /?, = 2-3/(2 + 3+5) = 0,6 Ом; по формуле (1.36), R2 = (5-2)/10=l Ом; по формуле (1.37), Лз(3-5)/10=1,5 Ом.

§ 1.24. Перенос источников э.д.с. и источников тока. На участке цепи рис, 1.28, а между узлами а к Ь имеется источник э. д. с. Е. Этот источник можно перенести в ветви / и 2, а узел а устранить и получтъ участок на рис 1.28, б. Эквивалентный перехид поясняется трас. 1.28,6. Точки с, d, b имеют одинаковый потенциа.! и потому могут быть объединены в одну точку Ь.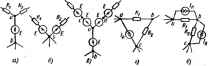

Рис. 1.28

Участок аЪс на рис. 1.28, г, между крайними точками а и с которого 1фисоединен источник тока h, может быть заменен участком аЪс рис. 1.28, д, отличающимся от участка рис. 1.28, е тем, что источник тока между точками с и с заменен па два источника, присоединенных параллельно и R. .-)кв1!валентность замены след;еТ нз неизменности значений токов в каждом из узлов. Тек в узле Ь не изменился, так как в этот узел добавили и вычли ток 7. Пракдь чески источники переносят при преобразованиях схем с целью Мх упрощения и при записи уравнений по методу контурных токов и узловых потенциалов в матричном виде (см. приложение Б).

§ 1.25. Активный и пассивный двухполюсники. В любой электрической схеме всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы независимо от ее структуры и сложности условно изоззнть некоторым прямоугольником (рис. 1.29, о). (Такой прием был использ<жан в § 1.17 без специальных объяснений.) По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представляет собой так называемый двухполюсник.

Таким оазом, двухполюсник -зга обобщенное название схемы, которая двуми выходными зажимами (полюсами) присоединена к выделенной ветви.

Если Б двухполюснике есть источник э. д. с. или (и) тока, то такой двухполюсник называют активным. В этом случае в прямоугольнике ставят букву А (рис. 1.29, а -в).

Если в двухполюснике нет источника э. д. с. и (или) тока, то его а-,мвяют пассивным. В этом случае в прямоугольнике либо не ставят якой буквы. Либо ставят букву П (рис 1.29, г).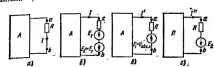

§ 1.26. Метод эквивалентного генератора. По отношению к выделенной веши при расчсте двухполюсник можно заменить эквивалентным генератором, э. д. с. которого равна напряжению холостого хода на зажимах выделенной веган, а внутрашее сопротивление равно входному сопротивлению двухполюсника.

Пусть задана некоторая схема и требуется найти ток в одной ее ветви. Мысленно заключим всю схему, сод)жащую э. д. с. и сопротивления, в прямоугольник, выделив из нее одну ветвь аЬ, в которой требуется найти ток / (рис 1.29, а).

Ток / ие [изменится, если в ветвь аЬ включить две равные и противоположно направленные э. д. с. и (рис. 1.29, б).

На оснопапий принципа наложения ток мож1ЯГпредставить в виде Суммы двух -IOK0B / и

/ = / + / .

Под током / будем понимать ток, вызванный э. д. с. £, и всеми источниками э. д. с. и тока активного двухполюсника, заключенными в прямоугольник, а ток / вызьшается только одной э. д. с. Eg. В соответствии с этим для нахождения токов / и Г используем схемы рис. 1.29, е, г. В прямоугольнике П схемы рис, 1.29, г отсутстют все э.д. с, но оставлены внутренние сопротивления источников.

Э. д. с. направлена встречно напряжению (/ ь. По закону Ома для участка цепи, содержащего э. д. е.,

r = {U.b~E,VR. (а)

Выберем El так, чтобы ток / был равен нулю. Отсутствне тхжа в ветви аЬ- эквивалентно ее размыканию (холостому ходу). Напряжение на зажимах аЬ при хмостом ходе (х. х) ветки обозначим t/oB .i.

Слещжатепьно, если выбрать EiUju-, то / = 0. Так как / = = / + / , а /=0, то / = Но ток / в соответствии со схемой рнс. 1.29, г определяется как

/ = EfiR + R. = UcbU{R + . J. (б)