При расчете цепи по второму способу нет необходимости строить результирующую в, а. х. всей пассивней части схемы. Учитывая, что уравнение IR+UncE в координатах / и Uc представляет собой уравнение прямой, проходящей через точки t=E/R; t/ = t/ c=0; /=0; Uhc - UE, провддим на рнс. 13.2,в эту прямую. Тангенс угла наклона ее к вертикали, умнаженн! на отношение m/m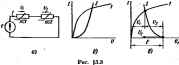

масштабов по осям, численно равен R. Точка нсжсетошя прямой с в. а. X. НС определяет режим работы цепи. Деистъитеяьно, для этой точки ток, проходящий через НС и R, одинаков, а сумма падений напряжений I/pc + = ПЯ1 нзментии э. д. с. от Я до прямую I=f(Uf.) следует пэеместить параллельно себе так, чтобы она исходила нз точки / = 0, t/=£, (пунктирная прямая на piic. 13.2, е).

Аналогично рассчитывают цепи при последовательжм соединении двух и большего числа НС. В этом случае сначала находят в. а. X. д)х НС, затем трех и т. д.

Рис. 13.4 Обсудим примнгаше второго

способа для расчета цепи рис. 13.3,ос двумя различными НС; в. а. х. ЙС/н ЙС2изображены на рис. 13.3 б. Так как НС2 нмеегнелинейную я. а, х., то вместо орямой I = f ((/r), как это было на рис.13.2,в, теперь нужно построить нелинейную зависимость IHi- Начало ее (рис. 13.3,в) расположено в точке 1 = 0, Ui = E. Отсчет положительных значений щхжзводится влето от этой точки. Так как положительные аначення на рис. 13 3. боткла-даваются в1фаво от начала координат, а на рис 13.3,в-влшо, то кривая I=f{U рис. 13.3, в представляетсобой зеркальное отображение кривой 2 рис. 13.3, б относительно вертикальной оси, проведенной через точку UE.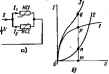

§ 13.5. Параллельное соединение

1ЫХ сопротивлений.

Схема параллельного соединения двух НС изображена на рис. 13.4, flee в. а. X. - на рис, 13.4, б. При построении результирующей в. а, х.

исходят из того, что нагфяжения на ИС1 и ИС2 равны н силу вх параллельного сомнения, а ток в веразвегвленной части схшы

Кривая Э рис. 13.4, б представляет собой я. а. х. параллельного соединашя. Строим ее следующим образш. Задаемся произволыю напряжением и, равным отрезку От. Проводим чмез точку т впи-каль. Складываем трезск pin, радный току в НС2, с отрезком тр, равным току в ИС1:

тп{-тр = тд.

Офезок тд равен току в веразветленной части цени при напряжении От. Аналогично опреиепяют н другие точки результирующ в. а. X. параллельного соединения.

§ 13.6. Последовательно-параллельное соеднншие

сопротивлений. На рис. 13.S изо(жена cxaia последсвагелыюго соединения НСЗ и двух параллельно соединенных HCi и НС2. Требуется найти токи в вегаях схемы. Заданы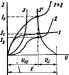

Рис. 13.5

Рнс. 13.6

Я. а. X. нелинейных сопротивлеинй (кривш /, 2, 3 рис. 13.6) н э. д. с. Е. Сначала строим я. а. х. параллельного соединения в соогВегстаии с методикой, рассмшршной в § 13.5 (кривая /+2 на рис. 13.6). После этого цепь сводится к последовательному соединению НСЗ и НС, имеющего в. а. х. 1+2.

Применяем второй способ построения (см. § 13.4). Кривая 3 рис. 13.6 представляет собой в. а. х. НСЗ, зеркально отраженную относнтельио вертикали, прсжеданюй через точку t/ = £. В точке пересечения 1фнвой 3 с кривой /+2 удовлетворяется второй закон Кирхгофа: t/s-ft/iaf. Сумма токов /i-h/a = /8.

§ 13.7. Расчет разветвленной нелинейной цейн влетодом двух узлов. Для схш, содержащих только два узла или ориводящихся к ним, применяют метод двух узлсю. Рассмотрим его иа пршлере схемы рис. 13.7. В схеме три НС и три источника э. д. с. Пусть я. а. х, НС изображаются кривыми рис. 13.8, а-в. Для опрезелшностн положим, что £i>£fl>£a- Выберем положительные направлшия для ток<ж. Пусть, например, все токн направлены к узлу а. Тогда, по

цвшу закону Кирхгофа,

Каждый из токов является ьжлинсйной функцией падения напри-жетня иа своем НС. Так, /, являетсяфункцией U, -функцией и, и /в -функцией t/j.

Выразим все токи в функции одного переменного -напряжения f/oft между двумя узлами. Для этого выразим t/ f/ Ug через э. д. с.

t/i = £i-V b; (13.2)

= (13.3)

иг=Ег-и\ь. (13.4)

Таким образом, возникает задача о том, как перестроить кривую it=fiUt) в кривую Ii=fiU b), кривую U = f{U - b кривую /,= ~fWab} и т. д. На 1ЖС. 13.9 показано, как нз кривой lfiV рис. 13.8, а получить кривую /i = f(t/ b)-точки соответственно обозначены одинаковыми цифрами.

Для точки 5 кривой рис. 13.8, я /, = 0 и t/, = при этом иь - El [см. (13.2)1. т. е. начало кривой lifiUb) сдаинуТО в точкуt/flb =

Росту Uj при L/j>0 соответствует убыль Ua. Для точки 2 прн UiEi [/аь=0. Росту Рис. 13.7 \Щ при t/i<0 отвечает рост U, причем

. и ь>-Е,.

На основании нзложашого рекадаадуется поступать следующим образом:

1) сместить кривую 7, = f(t/j) параллельно самой себе так, чтобы ее начало находилось в точке иьЕг (иривая, полученная в результате переноса, оредставлеяа пунктиром на рис. 13.9);

а) 6} В)

Рис. 13Л

2) провести через точку Uab=Ei вертикаль щшктириую кривую относительно вертикали.

Аналогичным образом производится перестройка кривых и для ;фугих ветвей схемы. Нанесш кривые Л (t/ b), UHta) и / = = f(Bb) на одном рисунке (кривые /, 2, 3 на рис. 13.10) и постротг

1 зеркально отразить

кривую /l-/s + a = Пtn6) (кривая 4 на рйс. 13.10). просуммирощм. ординаты кривых /, 2, 3. Точка т пересечения кривой 4 с осью абсцисс дает значение иь, при котором удоалетворяется J уравнение (13.1). Воссга- вим в этой точке перпендикуляр к оси абсцисс. Орди-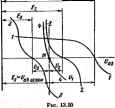

наты точек пересечения перпендикуляра с кривыми /, 2, 3 дадут соответственно токи /j, /д и /в по величине и по знаку.

§ 13.8. Замена нескольких параллельных ветвей, содержащих НС н . д. с, одной эквнвалштной. Положим, что имеется совокупность нескольких параллельных вегеей. содержащих НС и источники э. д. с.

фис. 13.11). Параллельные ветви входят в состав сложной схшы. не пЬказанной на рис, 13.11. Каковы должны быть э. д. с. и я. а. х. эквивалентного нелинного сопротивления НСЭ участка схемырис. 13,12, чтобы он был эквшалагген параллельным ветвям рис. lail?

Ощш ветвь рис. 13.12 будег эквивалентной ветвям рис, 13.11 в том случае, если ток / в неразвегалапюй части цени рис. 13.11 Hfffl любых значещ1ях напряжения иъ будет равняться току / в ветви рис. 13.12,

Воспользуемся построениями i№ рис. 13.10. Кривая 4 этого рисунка 151еистааляет собой зависимость /1-Ь/а+з=П бК т. е. является результирующей я. а. х. трех параллельных ветвей. Такую же в. а. х. должна иметь ветвь рис. 13.12, Если ток / в схеме рнс. 13.12 равен нулю, то t/ = £e. Следовательно, £9 на рис. 13,10 определяется напряжением t/ot, ори котором кривая 4 пересекает ось абсцисс. Лля огфеиелення в. а. х. НСЭ необходимо кривую 4 рис. 13.10 зеркально отобразить относительно вертикали, проведенной через точку т.

В. а. X. НСЭ изображена на рис. 13.13. Важно подчеркнуть, что включение э. д. с. в параллельные ветви привело к тому, что в. а. х. НСЭ стала несимметричной, несмотря на то что я. а. х. нелинейных сопротивлений /, 2, 5 в схеме рис. 13.7 были взяты симметричными.

Таким образом, изменяя э. д. с. в ветъях параллельной группы, можно изменять ее результирующую в. а, х, н как бы искусствапю создавать НС с самыми оричудливыми в. а. х.

§ 13.9. Расчет нелинейных цепей методом аквивалентного генератора. Если в сложной электрической цепи есть одйа ветвь с НС, то определение тока в ней можно производить по методу эквивалентного ген)атора. С этой целью выделим ветвь с НС, а &за остальную линейную схе представим в виде активнсно двухполюсника (рис. 13.14, с).

Как извесгао из § 1.25, схему линного активного двухпо-Fhc. 13.14 люсника по оптаиншю к зажи-

мам а и 6 выделаоюй веши можно представить в вцде последовательного соегщиения источника э. д. с. с э, д. с, равной наоряжению на зажимах оЬ при разомкнутой ветви ob(t/ 6 .!.), сотфотавления, равного входному сощютавлеяию i?* ли-HrfiBoro двухполюсника, н сопротивления ветви оЬ (рис. 13.14,6).

Определение тока в схеме рис. 13.14.6 ие представляет труда н можег прсеодиться в соответствии с § 13.4.

Прим 131. Определить ток в ветеи аЬ схемУ рис. 13.15 по мегаду эквивалентного генератора\]рн 1 = = 27 Ом; R= 108 Ом;

Ом; / = 54 Ом; £ = 70 В. В. а. х. НС изображена на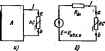

рис. 13.16. а.

Решение. Размыкаем ветвь и хода t/ s,., = 20 В.

Для подсчета входного сопро

[ напряжение холостого I iBi линейной части схемы

относительно зажимов оЬ необхощшо преоазоватьтрдтольник сопротивлений R, Ro (или Rt, Re. Ra) (рис. 13.15,6) в эквивалентную звезду (рис. 13.15, в) по формулам (1.35)-(1.37):

Rb= +fXii = J8 Ом; i?fl = 4,45 Ом;

Для определения тока в вешйоЬ схемы (рис, 13.15, о)на рнс, 13.Ш. о проводим прямую, проходящую через точки U = U =m В. 1=Q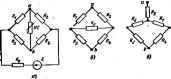

я t/-0. / = t/ 6 WB == 0,351 А (угол i наклона этой прямой к вертя-кали с учетом маоитабвд по осям равен Точка пересечения этой

ео ml Л;: eami /

D.1 о.г 0.3 B,s

прямой с в. а. X, НС (точка л) определяет рабочий режим схемы. Ток /-0,22 А.

§ 13.10. Статическое и дифференциальное сопротивления. Свойства нешшейнога сопротивления могут быть охарактизованы либо его в. а. X., либо зависимостями его статического и дифференциального ажротивленин от тока (напряжения).

Статическое српротивдение R, характеризует поведение НС в режиме немзвленного тока. Cteo равно отношению нааряжения на НС к прогорающему по нему току:

R-U/I. (13.5)

Сопротивление R численно равно тангенсу угла а менод осью ординат и прямой, идущей в точку Ь (рис. 13.16, а), умнонжннсму йа отношение масштабот по осям mi mj.