Е линии Zb и сопрои

> (лини*

на кшце разомкнута!).

Согласно рис, 12.4, а напр1тенне на кафузке равно удеоевн 1у напряжению падающей волны. Действительно, щ>и Z -*-oq

В соответствии с формулой (12.2Г) отраженная волна вапряжетвд - Ищ = ив-и 1-2но = и = и; в соответствии с формулой (12.20) отраженная волна тока Im = - u i/2 = - Таким образом, в течение второй ста;и процесса от конца линии к начаиу продвигается отраженная волна - Резуль-

тирующее состояние не линии отредьляется наложением первой падающей волны (ы, /щ) и пвой отраженной волны (ui, Ioi). На рис. 12.3, б дана эпюра распрецеления напряжения и тока по днини для некоторого момента вршени во второй стадии. (В этой стадии, для участков линии, на которые прошли отраженные волны, резульг тирующее напряжение равно 2н, а результирующий ток равен нулю.)

Третья стадия процесса состоит в том, что волна и , 1, дойдя до начала линии, отразится от генератора, как от короткшамкнутого конца линии (внутреннее сощхпнвлаше генератора принято равным нулю), и вызовет распространение в направлении от генератора к концу линии втсй падающей волны ( а, ( а), являющейся, по существу, спраженной волной по отношению к волне (uoi, ioi).

Для определеиия характера отражения волн от начала линии используем схему рис. 12.4, б. В ней Z = 0, 2ц>, = 2ы. Так как нагрузка Z =0, то и напряжение на ней равно нулю. Но напряжение на нагрузке в соответствии с (12.21) равно сумме напряжапи падающей волны (в данном случае Uoi - u) и напряжения отраженной от начала линии волны, распространяющейся от генератора к коту линии и потому названной второй падающей волной. Следдеательно, Ои+и. Отсюда

= - *п*=- Л = - Результирующее состояние на линии во время третьей стадш щю-цесса изображаю на рис. 12.3, в. Оно получено в результате навд1

жения трех волн: пе(шой падающей волны (и i,). первой отряженной от конца волны ( м. м) и второй падающей волны (и, i J.

Четвертая стадия процесса заключается в том, что на т[ж предыдущие волны накладывается четвертая волна, представляющая собой отражение от разомкнутого конца линии второй падающей волны.

Отражение второй падающей волны от конца линии щхжзсйдет Б соответствии со схемой замещения рис, 12.4, о, только вместо 2Ый=2м в сх йе будет вапрянише 2ti = -2и.

Вт<ая отраженная волна имеет Uoa = - и, Рельтирую-

шее состояние на лннйк во время четвфтой стадии (риа 12.3, есть результат наложения четырех волн:

г 1+и+i\ +% = i - i - *Ч-i = 0.

Таким образом, к концу четвертой стадии напряжение и ток вдоль всей линии равны нулю-линия приобретает такое же состояние, какое у нее было к началу первой стадии. Затем процесс повторяется до бесюшечиости, так как R и Со были приняты равными нулю. В действительности благодаря наличию сопротивления утечки Со колебателы1ый процесс постепенно затухает и вдоль линии устанавливается режим, соответствующий установившемуся процессу в линии при постоянном нагфяжении.

В рассмотренном примере линия на конце была разомкнута, поэтому отраженные волны имели такую же прямоугольную форму, как и надакицне.

Отраженные волны будут иметь форму, в общем случае не похожую на форму падающей волны, если в состав нагрузки на конце линии входят емкости и (или) индуктавности, а также в том случае, если в месте перехода с одной линии на другую есть сосредотсчншые

индуктивности и (или) ОйКОСТЯ.

§ 12.8. Переходный процесс при подклочеиии источника постоянного иапряж<я1ия к двум последовательно соединенным линиям при наличия емкости в месте стыка лииий. Пусть первая линия имеет длину i, и волнотое софотивлеиие Zm, втекая линия-длину 4 и ZeaZsj. Напряжшие источника э. д. с. равно и (рис. 12.5. с). В месте стыка линий есть сосрепоточенная ость С.

Требуется определить форму волны, (фоникающей во вторую лииию. характер изменения тока через сосредоточешую емкость, а также результирующее раофедБлгаие иапряжеяни и тока вдоль первой линии при движении по ней спраженной от стыка линий волны.

Переходный процесс надинается с того, что от генератора по первой линии распространяется падающая волна с прямсгольныч фронтом ni = w и im = H/Zri.

Для определения характера изменшия токов н напряжений, когда падающая волна дойдет до стыка линий, обратимся и схеме замещения с сосредоточжными памеграми (рис. 12.6, 6). В экА схеме

нагрузка образована двумя параллельными ветаями -емкостью С i волновым сопротивлением втсй линиигз.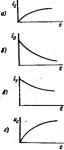

Две параллельные ветвн появилио! в схеме замещения потому, что в исходной схеме рис. 12.6, а падающая волна,дойдя до места сгака линий, встречает два пути для своего дальнейшего раофостраиашя: первый путь- ч(ез шкостъ С, второй путь-по второй линии с волновым С01фОТИВЛв1ИеМ Z.

Расчет переходного процесса в схеме рис. 12.5. б дает:

(12.24) (12.25)

Характер нзмздения i, U, it н с в функции от вршени изображен на рнс. 12.6. В первый мотлент после подхода волны в месту стыка линий напряжение падает до нуля. Рис. \2j6 незаряженная емкость для этого мо-

мента вршени 1д)£яставляет собой как бы ко-роткое замыкание. Начальное значение тока через емкость равно 2u/z. Затем емкость заряжается, напряжение на ней растет, >а ток чёри нее уменьшается. Ток te в схеме замещения представляет тобой ток электромагнитной волны, распространяющейся по второй линии; напряжете волны, растюстраняющейся по второй линии, равно isZ.

Для получения отраженной волны напряжения, распросфаняю-щейся по пвон линии в направлении от стыка линий к генераттфу, нз ордннат кривой рис. 12.6, г нужно вычесть напряжение падающей волны и затем перенести псхлучеиную кривую на линию, зная скорость отраженной волны.

На рис. 12.-7, а, 6 изображены соотаетственно отраженные волны напряжения и тока.

Эпюра распределения напряжшия и тока вдоль первой и второй линий для момента времени, когда отраженная от стыка волна дошла до середины первой линии, Нредстав-дена ссответсгеснно на рис. 12.8, а,б.

Перепад тока е/ в кривой рис. J2.8, б равен току через емкость для данного момента времени. По второй линии волна продвинулась на расстояние, вдвое большее, чт прошла отраженная волна по первой линии. Это объясняется тем, что первая линия кабельная, а вто-

Стштний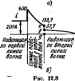

рая - воздушная. Скорость продаижения волны по воздушной линии 300-000 кч/с. а по кабельной-около 150000 кч/с*.

Пример 130. В схеме рис. 12.5, а z=50 Ом; z*=400 Ом; 1 = 100 км; С = 5.62 мкФ; /, = 60 км: й = 10 кВ; первая линия кабельная,-вторая воздушная. Построить эпюры раофеделения волн напряжения и тока вдоль линий для момента времени, когда распространяющаяся по второй линии волна дойдет до конца второй линии.

Решение. По формуле (12.28),

50+400 4000 I

Р- 50-400.5:62-10-*- *

Ток падающей волны по первой линии

- i H/z = iov50=200 -А.

По формуле 024), i,=.44,5(l-е- ) А. График i,=f{f) нзо-

А. График предргавлен

бражм) на рис.

По формуле (12.25). ia = 400e- на рнс. 12.6. б.

По формуле (12.26J, i, = 44.5(l-н8е ) А. График тока изображен на с. 12.6, е.

По формуле (12.27), с = z = 17750(1-е- ) В. Кривая ос изображена на рис. 12.6, г.

* Формуле для скорости v движения волны по лиииц и вхсцящив в нее Lo и Q приведены в § 11-10.

По условию, падающая по второй воздушной) линии волна должна дойти до конца вгарс линии. Расстояние }=Ш км она пройдет за время i = Vi;= 100/300000= 1/3000 с.

За это время отраженная от стыка волна пройдет по первой (кабельной) линии расстояние, в два раза меньшее.

Графики распределения ни/ вдоль линии изоажены iA рас. 12.8, а, 6.

Перепад ef на рис. 12.8, б равен току при i= 1/3000 с: Is = = 400е-*з 106 А.

OipeK fg равен току ij при i = 1/3000 с: 144,50-*) =

Отрезок тп на рис. 12.8, с равен напряжению ис при i= 1/3000 с: с =-13,05 кВ.

В рассмотренном примере электрическая цепь, содержащая линию с распределенными пираметрами, подключалась к источнику постоянного напряжения.

Однако часто встречаются цепи, в которых э. д. с. нсочнтжа изменяется по сннусоидальиту закону во времени. Если длина линии с распр€деле1шымн параметрами и частота синусоидальной э. д. с. таковы, что время пробега волны по линии (I = l/v\ много меньше пиода Hq>€H№Horo тока Т, например составляет величину порядка fH-J 7*.

то при исследовании пфвых стадий п ехоциого процесса в первом грубом приближении можно принять, что линия подключается к источнику постоянной э. д. с, которая равна амплитуде синусоидальной э. д. с, (расчет ва наиболее тяжелый случай). Если же время пробега волны по линии составляет большую, чем (-s-J, часть

периода, то при расчетах необходимо учитывать изм№снне э. д. с. источника при перемещении падающей волны по линии.

Пра отключении нагрузки или ее части в линиях также возникают переходные процессы. Расчет нх производят на основанин принципа наложения, включая в размыкаемую вегаь источник тока, который дает ток. равный и противоюложно направленный току в размыкаемой ветви (см. 8.59).

Результирующие волны тока и на1Ч)яження на всех участках лннии; находят наложениш на волны тока н напряжения, ког(фые были на линии до отключения ветви, волн Юка и напряжения, продвигающихся от места размыкания в €хгтальные участки линии.

Лри пгктнении в каком-либо меапе линии новой ветви токи и напряжшия в эт(А ветви находат методом швивалешям-о генератора, а токи в остальных участках линии -методом наложения.

§ 12.9. Линия эадЧ)жки. Под линией задержки, орима1яемой в импульсной технике, понимают устройство, которое включают мовду источником сигнала и нагрузкой, служащее для задержки поступления сигнала в нагрузку на некоторое заданное время В простейшем случае (ори малом линию задержки выполняют в виде куск? коаксиального кабеля длиной I. Он создает задержку t = llv. Если

хотят получить относительно большое i, то используют цепочку из п каскадно соединенных одинаковых льтрзв низкой частоты (см. рпс. 5.1, а), выбирая параметры L к С фильтров так, .чтобы полоса частот сигнала Q - u> находилась в полосе прозрачности фильтра н

чтобы о<<В2, где сц -частота среза фильтра. Параметры фильтра согласуют с нагрузкой Е =УЩС. Вшя задержки tf п{йЫй&) = пУШ.

Выведем эту формулу и в более широком плане обсудим вопрос о времени задержки сигнала при прохождении го через четырехлолнхшш.

В § 9.4 было гажазано. что передаточная функция четафехпшюслнка К (/и)= = Ca(/co)/Ci(/ )=f (/ш)е/ч , пропускающего сигнал без мшвжеиия. но с задержкой во времени, должнд обладать двумя свойствами: 1) модуль

ХКаЩ 1 = const (в частиостн. равен единице)

2) аргумент ф(й.)=-Ы;.

Применительно к фильтру ?((/ь>)=1/ее=1еЧеД. Сопосгавлешк характеристик филыра с характернстикамн шреиюлюсинка для аокы прозрвчиоста дает;

А:(/ )1 = 1/е =1. *=-ф(ы)=<. Для фильтра НЧ рнс. 5.1. а в зоне прозрачности *=агссо5 А =arccos (1 -t#LC) нелинейно зависит ог ш. Для определения времени задержки грвближенно заменим ату нелинейную зависимость пряыак с угловым в(аф((шше11Тои. равным

Тогда время задержки, создаваемое одним фильтром.

(-26)tC)-

Если в

J n фильтров НЧ. то Бремя задержки в п раз больше!

QCHHK, представляет собой кодот-

Если сигнал, проходящнЙ через чет1 кий импульс, то его частотный спектр весьма широк и четырехполюсник в orain-чне от линии с распределенными параметрами не а,состоянии пропустить без затухания колебания всех частот. В этом случае можно только условно говорить о времени задержки, понимая под ним усредненную производную Ab/dat. подсчитанную для основной ч------

□ спектра.

§ 12.10. Испат.зованне лиянй для 4 На рис. 12.9, а изображена мена, п. Импульсы тока в нагрузке Jh- В с

финровзнйя кратковременные импульсов.

эволяюншя формировать прямоугольные

, - - -. - 1 имеется источник постоянного тока / и

. j линии. При размыкании ключа от источника тока / по первой линии длиной / с волновым сопротивлением Zg распространяется прямоугольная падающая волна тока 2 н волна напряжения IZji. Дойдя узла а. волна частично пройдет во вторую н третью лнннв н частично отразится. Дтя определении волн, прокоцящия RO вторую и третью линнн. служит схема аамещеиня рис. 12.9. б. 11з нее следует, что /j- 4 я /,= 2.

По второй линяй распространяется волна(/,=/21в.потретъей O.SZo-

Волна (/д. дойдя до конца второй лниии, где включена нагрузка /=2, погло-ьцается в ней без отражения.