по ;с н (12.2) по fc

В соответствии с (12.4) в правую часть (12.3) вместо di/djcdi подставим - и обозначим LaCo=l/vb -

(12.5)

Из предыдушйт) [см. § 11.10, фсфмула (1КЗ£)] известно, что v=> - I/]/ LoCq есть скорость распространения электромагнитной волны по

линии. Если уравнение (12.2) прор по f н в правую часть пр ставить правую часть получим

. [рсдаать по х, а (12.1) - !ного уравнения (12.2) под-уравнения (12.1), то.-

(12.6)

Равенства (12.5) и (12.6) являются уравнениями второго порадка в частных пронзводаых. Из курса математики известно, что уравнения такого вида называют волновыми.

Решением уравнения (12.5) является сумма любых функций fi и причем аргументом функции Д является (). а аргументстл фуш1цни/ -(-1-):

Для ожращения записи в дальнейшш буем сбсвтроаы

u.~u[t~]: (12.6)

<fe-/,(<+f)- . (12.9h

Следовательно,

и = + Ио. {\2.Щ

где индексы во и кп означают отраженная и падйюв (волны).

Вид функций и /а определяется граничными условиями в начале и конце линии. Функции и в общем случад должны позволять даажды ;ф)фффенш1рсшгть их по х и

Подстановка функций fi{t- и

h[t-¥~) в (12.5) дает тождество.

Решение уравнения (12.6):

* = Р.(-~) + Ф.( + ). (I2.ll)

Для сокращения записи обозначим:

tr,*h{t~~). (12.12)

о = Р2(+)- (12.13)

Тогда

* = (12.14)

§ 12.3. Падающие н~ отраженные волны ца линиях. В соответствии с формулами (12.7) и (I2.ll) напряжение и ток в линии могут быть прсдетавлнш в виде двух функций: функция h[t~) и <Pi(-J)-задающие волны; функции-j-) я ф от-

раженные волны.

Пехающие волны пч)емацаются со скоростью v по направлению от источника smeprHH к приемнику, т. е. в сторону увеличения координаты х; (Сраженные волны-от приемйика энергии к источнику, т. е. в сторону умншшеяия координаты х.

Обсудим, кйк следует понимать, что аргументом функции /i является ( -(аналогичные выводы можно сделать и по отношению к другш* функциям). \

Пусть в некоторой точке линии x=Xj при t=ti значение функции у) равно Это значение функция Д будет принимать во всех точках линии, где л:>х, с запозданиш во времени, равным {х-х/о н обуслжлеиным конечной скоростью перемещения волны по линии.

Так, в точке значение функции /, будет равно при i =

= 2 = i+~- Дейсгвительно,

/.(>-)-A(.+--) = ft(4-l)-f..

Таким образом, каков бы ни был закон изменения напряжения падающей волны в начале линии, по такому же закону, но с запозданием во времени изменяется напряжение падающей волны в любой точке линии.

§ 12.4. Связь между функциями/i, /j и функциями Vi, Фг- Найдем связь между функциями fi и ф, а также Д и щ. С этой целью в (12.1) и (12.2) подставим (12.7) и (12.11) и для сокращения записи обозначим:

=fi:

Toma уравнение (12.1) дает Из (12.2) следует, чю

<r;-<A=CJi+CJi. (12.16).

Перетпоем (12.14 я (12.16):

- -.(Й + Й; (12.1Б

/;+К-.(Ч>;-!Й. (12.16>

где Zb-волновое сопротивление однородной пинии б© потерь Ген]

формулу (Н.23а)]. И

Таким сказом,

?:-К=2.(<р;+фЭ:

(12.15( {12.161

(12.171

ф;=-К/г . (12.1

Если ирдаиведение двух фташлй (напрша, ipj н fO при значениях х и t равны, то это значит, что сами функвди {щ и /, равны с точностью до постоянной. Поэтому

(12.1! (12.2П!

Постоянные интегрирования опустили, так как полагаем, что в ю ках и наоряикяши ошакшей н (лрамсешой волн опдгтствукт посеянные составляюшле, не аавасящие от х и от . Два шхаедних ypi нения можно переяисап. с учетом (12,8), (12.9), (12,12), (12.13):

/- = /2.: (12.1Г

f=-iijZ - (120

Из (12.19) следует, что тж падающей волны для любого момен времени и для любой точки на линии ранен частному от деления н пряжения падающей волны для тото же мснлента времени и для то( же точки линии на волновое сопроттление.

Из (12Ж) вытекает, что ток отраженной волны для любого н! мента Бршени и для любоЗ точки лини11 равен взятому с обращу

знаком частишг от деления Hanj

1 отраженной вошы в той же

Рис 12.1

точке линии и для тога же MOhtenra вршени ка вошовое сотфотив-ление. Ъаш минус в (12J26) означает, что ток о1ражЕ1шой волны направлен встречно положгаедьишлу навленшо отсчета тсжа, показанному на рис. 11.2.

§ 12.&. Элжтромагннтные процессы при движеиии ямоуголь-ной волны во линнн. Пусть источнни постоявного ванряжения U,

цмекяцнй штреннее ешропшкиис; равное нулю, подключается к незаряженной однородной линии с распределашыми параметрами, у котвр(А Яд = 4=0 (рнс. 12.1).

По линии нфемещаетея отдающая элек-тромагнитиая волна. Начтаыб участок волны, П1фвш1 цюдаш-аовднся ио линии, принято называть фронтом волны. В данном слу чаеволна имеет прямоугоньный фронт.

Двигаясь по линии, волна создает между проводами линии электрическое и магнитное ноля.

Гиращевие магнитного потока (нотсжосцшления) на фрште волны за время равно проажедению тока i на индукпшность участка линии длиной dx: d = iLodx; оно вызывает э. д. с.

=-i ]/=-iz,=-ы =-и.

Джим оазом, иа <:ите ваш возвшеает д. с. eaм щдyкцffl численно равная нап1Яже*дао генерат(. На фронте вошы происходит зарядка проводов линии: один провод, ншрю4> sfpXHHH, присоединенный и п.шх:у исю<тшса . м, с, ГфиоСает пояожшсльиый заряд, друшп (нижнян>-отриоагельЛ З9рял (гакой же величины).

Кроме того, иа фронте волны возникает ток смещЕятя idq/dt, где d -ирйраще*ше заряда на ом из щнводвв лннш за время Л: ЙА>= CoadxCoOvdf.

Проходящий по диэлектрику на фров№ всшны ток смшютвя равен току падающей волны, проходящшу по проводам линии:

Электро

ic = dg/dtCoiiv = ujZi. 1ял ваша, продвигаясь тю линии, канщой иице

Линии сообщает энергию электрического поля /2 и энергию магнитного поля Loifj2. Можно пжазать, что эта количества энергий равны. Действительно,

-ледсважелыю.

Когда падающая волна достигает конца линии, к которому в случае п]жсоединена некоторая нагрузка нли другая линия (с друге волновым сопротивлением), то часть падакяней волны проходит в г грузку (или соответствапю во вторую линию), а часть отражается возникает отраженная волна.

Чтобы выяснить, какова форма волны, проходящей в нагрузку какова форма отраженной волны и как онн деформируются во мени, применяют расчегную схему, которую принято называть схемп замегцения для исследования солноЫх процессов в линии с pacnpeir ленными параметрат.

§ 12.6. Схема замещения япя исследования волновых процеом* в линиях с распределенными параметрами. Для обоснования мет .) днки сосг№лацЯ схемы замоценин обратимся к рис. 12. л На im изображена линия с распределшными парамефамя, на конце KOrcni

включена некотсч)ая нагрузка. Начиная с того момента, когда падаю-; щая волна дойдет до конца линии, по нагрузка пойдет ток i\, и на ней будет напряжение

На рис. 12.2, а изображены эпюры волн ы и i на линии для мо-: мента 1фшени, непосредсгвишо предшествующего поводу к концу линии.

В соотаегствии с формулами (12.10) и (12.14) напряжение и ъ в любой точке линии можно представить в вчде суммы падающих отраженных волн. Это справедливо также в отношении напряженж и тока Б конце линии. Следовательно,

(/ -Ь = и ; (12.211

Звменив 1 на ujZ , а на - ujZ , получим

+ = в; I, - о = ae

2u = u + i Z (12.2

Таким образом, напряжение на конце линии и и ток в нагрузке яеэашкнио от хч>актера натуэки связаны с наоряжениш

волны Ып уравнением (12.2. Последнему соогвггвует схема с сосредоточенными параметрами, изображенная на рис. 12.2, б. В ней к источнику 9. д. с. вапрнжшием 2ы подключают последовательно оюднн -ные и Zg.

Расчет переходного процесса в схеме с сосредоточЕнцыми параметрами (рис. 12.2.6) пронзаодится любым из методов, рассмотреднья Б гл. 8. Расчет дает возможность определить /=/(0 и Ия=/(0-После того как эти зависимости найдены, можно определить характф изменения во-бремени напряжения н тока отраженной волны: Ио=/(0 и /о=/(0. Действительно, из уравнений (12.21) н (12.20) сдедуег, что

ио(0 = е(0-ио(0;

= (12.21)

Рассмотрим несколько примеров, иллюстрирующих применение схемы замещения.

§ 12.7, Подключение разомкнутой ка конце лиинн к источнику постоянного напряжшия. В линии без потерь, так же как н в колебательном контуре без ноть, при подключении .к источнику постоянной э. д. с. вш- никают незатухающие колебания. Период колебаний состоит из. четырех частей нлн стадий (рис. 12.3} одинаковой продолжите-лмосги 1/v, где f-длина линии, и -скорость распространения волны. Для рассмот-ршия этих стадий воспользуемся двумя различными схемами замещения. Первая схема (рис. 12.4, о) соответствует разсмкну-тому концу линии (Z = co), когда к нему подходит падающая от начала линии волна. Вторая схема (рис. 12.4,6) соответствует моменту времени, когда отраженная волна подошла к началу линии, где вклю-.чен генератор постоянного напряжедия, внутреннее сопротивление которого пола-гаия равным нулю (Z =0).

Рассмотрим каждую из стадий процесса в отдельности.

Первая стадия. От генератора к концу линии распространяются волна иапряжения ы 1=U и волна тока i j = u/Z = i (см. рис. 12.3,л).

Вторая стадия заключается в тш,.что Рис- 2.3

от конца линия к ее началу движется отраженная волна (u i, Для определения u i и служит схема рис. 12.4; а. Ояа составлена в соответствии с общим метсдом, изложен-Hbw в § 12.6. В ией к иапряжению 2аи1-2й. тодкпочаются волно-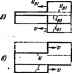