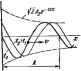Рис. П.Б

лжа {второе слагаемое формулы (L].38)]. Отраженная £ пая волна образована отраженной волной напряжшия [первое , гаемое формулы (II.37)J к отраж волягЛ тока [первое слагаемое фор! (11,38)].

Знак минус у отраженной волны i ка свндетельстеует о том, что ы тергпи, который акет ссобойотри пая эж1пр<ж(агннтная вдлна. , в- обрагЕюм направлении по cpJ с потоком энергии, который несет бой падакэздая волна.

Каждая имтгоншга падающей ны (волна напряжения или волна * ка) представляет ссйой cHiiycoHja>Liii колебание, амплитуда которого > шается по мере роста х (множитель е**), а аргумент является ( цией времени н коорддааш х.

Каждая компшента отраженной адастрсиагншж* волны тукает по мере продвижения волны от конца дннии к началу (mi житель е-). Физически эффект уменьшения амплитуд падающей и отраженной ваян по мере нх пр)данжяшя по линии объясняется наличием потерь в линии.

На рнс. Н.5 изображены графики распределения падающей волны напряжения вдоль линии (в функции х) для двух смежных моментов времени: и а>А. Падающая волна распространяется слева направо. При построении принято -[-* = О,

На рис. 11.6 представлены графики распрсдедения i волны напряжения для двух смежных моментов врклши: ta i Офаженная волна раофостраяяется справа налево.

ного зового состояния. Если

Рис. 11.6

§ 11.8. Ко

5, .ччяцт отражения. Ошсмненне напряжения . женной волны в конце линии к напряжению падающей волны в а линии называют коэффициентом отражения по напряжению и t начают Л . В соответствии с формулой (11,34)

Гфн согласованной нагрузке / = 0. рв холостом ходе Кш-Коэффициент отражения по току fCj--Л .

§ 11,10, Фазовая скорость. Фазоеой скоростью называют ( рость, с которой нужно перемещаться вдоль лишш. чтобы набвд одну н ту же фазу колебания, или иначе: фазовая сксрость-

скорость веремйцения по лишт .

Аяза падающей волны напряжения нетленна, тоВ соответствин с формулой (11-37)

Возьмем прсизводную ш времени от обеих частей последжго равенства:

-iL(cf+ -P4=e, ИЛИ o.-pf = 0.

Отсюда

Пример 116. Найти фазовую скорость для всйвушнойдаухпроводюй

линии с малыми потерями.

реш ение. Из фсрклы (П.22 а) следует, чтор = вУЦСь- Поэтому

Индуктивность едшицы длины двухпр(водной вдадушной линии [см. формулу (2.10)]

где ро-магнитная постоянная; d-расстояние между осями проводов; г-радиус каждого провода.

Емкость едииины ддйиы воедушной лгухщкшцдвой лишш [ом. формулу (19.43)1

Сь=-, где Be-электрическая постоянная.

Фазовая скорость

§ li.lt, Длина волны. Под длиной волны К тншаш рясстояние, на которое распроораияегся волка за один период Г= 1 ;

>.= vT=vJf. (11.40)

Пример 117, Haihn дшшу апапрошпшшой волны при f=60 в 50-10Гц.

Решение. При f-60 Гц

При/=60.10ТцЯ-6м.

§ И.И. Лишш ee3miatKe 4>.JImia6esiia acmuu грежпвляег линию, вдоль которой волны всех частот распространяются с одинаковой фазовой скоростью и затухают в равной стеиени.

При движении алектромагннтиой волны по линии без искажений олны напряжемш и тока уиеяьшаются по ашшигуде, ио формы воли

напряжения в конце и начале линии подобны; точно так же г формы волн тока в начале и конце линии, , ,

Неиекажающие линии находят применение в телефонии. При i фонном разговоре по таким линиям не искажается талбр ranoca,.,-d не искажается спектральный состав голоса.

Для того чтобы линия Выла неиа4ажающен, коэффициент ; ния а и фазовая скорость не должны зависеть от частоты; ( не зависят от частоты, если между параметрами линии имеет , следующее соотношение:

/г / =сл, (11:

Для сокращения записи обозначим RLi=Co/Co=k. По oof лению, y = a-i-iP=VZiX . Но

n = Ge+/o)Co = Co(ft + /o)):

Следовательно,

Из формул (11.42) и (11.43) следует, что кгаф(1ищиент зату: и фазовая скорость Рф в линии без искажений дейсшителыю не сят от частоты.

В линии без искажений волновое сстротивлаом!

является действительным числом и также ие зависит от частоты.

Чтобы убедиться, что форма boj иадобна форме волны начряжеявя i в оде линии в виде суммы двух снну< частоту ю. а другое 2&,---------

составим выражение цля-щ. Пусть

sin ( (+VO-f Сяя, Еш (Зм+ф,

Так как для линия без искажения кгаффициент затуханк часюты [см. формулу (11.41, то амплитуды toax колебани! уиеныпаются в одинаковой степени и становятся ретнймв без искажения (вффициент фазы р

в конце линии Ug полн . Ill, лоьмен яапра 1.ЧДНО из lyiTo,

Для Л;..........

поэтому длй частоттл 2© к

гновенноё значение т

раза больше, чем для част f фяженйя в хонце линии

Вынесем е- за скобку и .обозначим время /-т-- черед ж- Получим Изе-о [Ui sin (ют-1-+£/я5, sin

Если сопоставить лать вывоа. что вшр*

е с выражением для и, то i

I в конце линии вмеет ту же форму, что я напряжение

j уменьшено по амплитуде за счет затухания я сме-

щшо во времени на р11а=1/Ь -на время движения волны по линии длиной /.

§ 11.13. Согласованная нагрузка. Линия с pacnj

метрами, как пржнло. служит в качестве промежуто11ного звена между источником энергии и нагрузкой.

Обозначим сопротивление нагрузки ZsiZiOI. Если ZnZ,. то падающая волна частично прейдет в нагрузку, частично отразится (Я нее (возникает отраженная волна).. Часто берут ZZ. Такун! нагрузку называют Согласованной; при ней отраженная волна отсутствует. В этом можно убедиться с помощью формулы (11.34). Дей-сгвителыю, отраженная волна отсутствует, так как Ах = 0:

Л. - 0,5 (О - /fiZJ е = 0,5 (О - 0 е = 0.

§ 11.14. Определение напряжения и тока прн согласованной нагрузке. Чтабы получить формулы для оПредрлення напряжения и тока в любой точке, удаленной от конца линии на расстояние у, Б формулы (11.35) и (11.36) вместо Z подставим Z, заменим /sZjHa Ci, и UfZ на /а. Получим:

ОС/ (ch УУ+ dl w) = fsew;, / = /.(chvj+shTi) = 4e В начале линии при у = 1

t7, = f>,ev=f/,e*e e ;

(11.44) (11.45)

(11.46)

где f/fi-модуль, а fpu, apryMOiT комплиса 0. /а -модуль, а ф/.

аргумент комплекса

§ 11.15. К

, , :нт полеяюга действия линии передачи прп согласовшной нагрузке. Коэффициент полезного действия линии передачи равен отнсмпению активной ьюшлости в конце линии к активной мощное в начале линии Р:

Яв = ад cos (фи, - 9; J = ии cos

где фв -apryMOiT волнового сстротивления Zg. -

Г\рн согласотанной нагрузке угол между (j\ и 7, также равен ф поэтому в соотаегствии с формулами (11.46)

Pl =. cos Фа = t/g/aC* COS фг

Следоватешю,

ri = Pp=.l (11.47)

§ 11.16. Bxojuioe сооротивлолю нафуженной лняии. На рис. 11.7 Изображена схема, состоящая из источника напряжения /7 линии с раофедедашыми параметрами длиной / и нагрузки Zs Входное

шрогаююши; Z .Ujl,. В Лещж (11.Э5> и (11.3% подставим t и заменим на Ij:. Получим

Если нагруви ижлаоовши fr.- е. г -ДА -т т (11.48) что входное со1фо№ажн11е рар ----

7 ZjfajTf+Ai*)

§ II.J7, Определение вапряжении н тела о линии вез похчим!

Строго г гввря, линий без ноярь ие ствует. Однакв- можно соагдать лияию е г . малыми нежрямя (с очень игаяыми

по сравнению с isLt, н иСо еоаввектвенниП Л и распростравить на нее теорию линиЦ Ш без потерь.

Из предыдущего [см. фмулу (U.I

извесгао, что если ,=t=0j,TO. Рнс, II.7 Y= +/M/ VXA.

т. е. коэффициент затухания а- О а ксффвииент фазы P=-giVZ \ Прн этом волновое сопротивление 2=YitJCu является чистЬ

активным [см. формулу (11.23 afll

Для определения напряжения О и тока У в любой точке линии

эбратимся к формулам (11.35) и (М.Зб):

Учтем, что ytf (а + /р) = (О + }Щ у = /ру.

Гиперболический косинус at мшмого spsystmtai /ягршенкругюшу ( tocHBjicy ©г чраумеша х:

ch ix = 0,5 (в*+е*) = 0 (cos X + / sin X+cos X - / sin л) = cos x.

Следовательно, chYj*=c!ijPj(=cosPi/. 1

Гиперболический синус от аргумента равен круговому синусу гг аргумента х, умноженному на j:

sh /г = 0,5 fe**-е*) = 0,5 (cos х+/ sin* - cos л: / sfn л:)=/ sin х.

Следовательно, syx&bjyjbiny.

Поэтому для лшша без иощ>ь формулы (35 ж вере-

сйшем сяезиуюшям образом:

(И.35) (iJ.36)

линия без потерь при холостом

§ 11.18. Входаое а

ходе. При холостом ходе UQ. Поэтому

top*

ix. (П.49)

Исследуем характер йявмвтя ври изменении расстояния и

от конца ляини до текущей точки на вей.

В ингерваж значений ру т О де я/2-fePs вэиеняется от О до со, поэтому г 1,., имеег елкосгный характер (множитель-/) и по модулю

На рис. 11.8, а расположение

крттой выше оси абсцисс соотвег- I I

ствуетмндуктиБномухч)ак еруреак- А \

тивного сопротивления линииX,ни- - - 1 ЬьД

же оси-еикостнсму. Ввнтервале значений pj/ от я/2 до я 4 отрицателен и изм(а1яется от - то до О. поэтому аменяегся ш модулю от О до то и имеег индуктивный характер (множитель 4-/7 и т. д.

Таким образом, шмишя дднну отрезка линии без потерь, можно имилфовль енкосхное и mjxm-

Тис. 11.8

пое соютивлшия любой велучины. Гактичеои это свсшсгао ио-пользуют врн высокой чаооте в различных радиогеэин(чеа*их установках.

§ 11.IS BxQiHioe отротивмияе дннин €вз пАшрь (фн коротком Замыкании иа конце линии. Прн коротком замыкании на коьоелинш! f в=0м из ф(Ч мул (I i .35 ) н {i J. 36) следует, что йходное оочютнвлшне

2 ,. = /Z,tgPi, = /l/i;?E;tgft,. (11.50)

где р=в/ад.

Будаи мять длину отрезка лшнш у и носл1м змистер кзиь-нения входного озврсгтыкша.

В интервале значений Pjf от О до л/2 поаожязсяш в изменяется от fi да сжижательйю, й этом нив 5>вале вэнэдное отротнв-леше имеет лйздбтжшш :шаш>ш и юисюшязяегаезся отфда то (рис. 11.8, б).