Доказательство этого состшшаат проводится аналогично приведенному ранее.

Пример 10. На рнс. 1.20 изображена схема, в которой ввделены три ветви. В ветви 1 включен амперметр >4 в ветви 2 -амперметр Ля. В ветви 3 имеется ключ /С и сопротивление R. Если К разомкнут, то Л, показывает I А. а - 5 А. При замкнутом ключе амперметр Ai показывает 2 А, а Лв - 4 А. При замкнутом ключе сопропшленне Rg изменили так, что показание амперметра As стало 4,5 А. Каково показание амперметра в этом режиме?

Решение. Вьфазим через 1:

иа+Ы,.

Составим два уравнения для определения а н Ь:

I=fl!+5b; 2=а-ь4Ь. Отсюда й=6 и Ь=-I.

При./я = 4.5А /1 = 6-4.5.1 = 1,5 А.

§ 1.19. Изменения токов ветвей, вызв;

тивления Одной ветви (теорема вариаций). На рнс. 1.21, а выделим ветви i и 2 с токами /i и /а, заключив остальную часть схемы вместе с источниками энергии в прямоугольник А (активный); проводимости g,j и полагаем вжесл1ыми. Пусть сопротивление ветви 2 изменилось на &R (рис. 1.21. 6), в результате чего токи стали Л-ЬА/, и /-f A/j- В соответствии с теоремой компенсации заменим &R ка э. д. с. AE = AR (/а+Д/а), иаиравла1ную встречно току/g. На основанин принципа наложения можно сказать, что приращения токов Д/, и Д/а вызваны э. д. с. Д£ в схеме рис. 1.21, в, в которой часть схемы, заключенная в прямоугольник, стала пассивной (буква П). Так как схема внутренних соединений и значения сопротивлений в схеме прямоугольника оста-

Рис, 1.20

а) t) 6) Рис. 1.21

лись без изменений, то проводимоста gii н Д- схемы рис 1.2,в

имеют те же значения, что и в схеме рис 1.21, а. Для схемы рис.

1.21, с имеем:

Д/,-А£&.--£ ДЛ (7,+Д ;

А/.= Д£е =-е дк (7,+ли

(1.15)

Соотношения (1.15) позволяют определить изменение токов в ветвях 1 и 2, вызванные изменением сопротивления в ветви 2.

§ 1.20. Замена нескольких параллельных ветвей, содержащих источники 8. д. с. и источники тока, одной эквивалентной. При

расчете сложных схем существенное облегчение дает замена нескольких параллельно включенных ветвей, содержащих источники э. д. с. и источники тока и сопротивления, одной эквивалентной ветвью.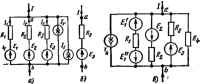

Участок цепи рис. 1.22, б эквивалентен участку цепи, изображенному на рис. 1.22, а, если при любых значениях тока /, подтекающего из всей остальной, не показанной на рисунке части схемы, на1Ч)яжение на зажимах о и Ь (иь) в обеих схемах одаиаково. Для того чтобы шиснитъ, чему равняются R н составим уравнения для обеих схем.

Для схемы рис. 1.22, а

/i = (£, - U t)/Rt = (£i-(/ fc)&: h={E,~U t)g2l

(1.16)

I. = {E,~Uab)gn.

Следовательно,

fttTi *=i *=i *-i

где n -число параллельных вегеен с источниками э.д.с; ? -число ветвей с источниками тока. Для схемы рис. 1.22. б

/ = £,-t/ 6g (1.17)

TAeg=l/R,

Равенство токов / в схемах рис. 1.22, а, б должно иметь место при любых значениях (/о> это возможно только в том случае, когда коэффициент при иь в (I-I7) равен коэффициенту гфи (/ ь в (1.16). Следовательно,

(1.18>

Но если слагаемые с Уь в (1.16) и (1.17) равны и токи / по условию эквивалентности двух схем также равны, то

(1.19)

Формула (1.18) дает возможность найти проводимость и по ней Л, в схеме рнс. 1.22, б. Из формулы(1.18)видно.чтопроводнмосгь, не зависит от того, есть в ветвях схемы рис. 1.22, а э. д. с. или нет.

При подсчетах по фq)мyлe (1-19) следует HKferb в виду следующее: еслн в. какой-либо ветви схемы э. д. с. отсутствует, то соответствующее слагаемое в числителе (1.19) выпадает, ко проводимость этой ветви в знаменателе (1.19) остается; если какая-либо э. д. с. в исходной схеме имеет направление, обратное изоаженному на рис 1.22, а, то соответствующее слагаемое войдет в числителЕ* формулы (1.19) со злаком минус.

Ветви схемы рис, 1.22, а и ветвь схемы рис. 1.22, б эквиватентны только е смысле поведения их по отншкмпо ко всей остальной части схемы, не показанной на рисунке, по они не эквивалентны в отношении мощности, выделяющейся в них. Качественно поясним это. В ветвях схемы рис. 1.22, а токи могут протекать даже при /-=0, тогда как в ветви аЬ рис. 1.22, б при / = 0 ток и потребление энергии отсутстщют.

П{№мер II. Заменить параллельные ветви рис. 1.22 в одной эквивалентной. Дано: £1 = 10 В; £,=30 В; £ = 40 В; £а = 60 В; = 2 Ow; Дв=4 Ом; Rsl Ом; =5 Ом; Ь = 6 А.

Решение. Находим:

gi = 0,5 См: ga = 0.25 См; gs=\ См; = 0.2 Сч:

т-оГ5-г.о.25-ц-ю.2-Р-53 Ом: 21 В

Д gfegt (10-30).0.540O.S5-b60-1-6 g

Таким образом, параметры эквивалентной ветви рис. 1.22, б Яй = 0,513 Ом н £,= 18,4 В.

§ IJZI. Метод двух.узлов. Часто встречаются схемы, содержащие всего два узла; на рис. 1.23 изображена одна из таких схем. Наиболее рациональным методом расчета токов в них является метод двух >Злов.

Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем токи ветв) принимают напряжение между двумя узлами схемы.

Расчетные формулы этого метода получают иа основефсфмул (1.16) и(1.16): их также моею просто получить нз более общего метода - метода узловых потенциалов (см. § 1.22).

В отлйчне от схемы рис. 1.21, о ток / к узлам а V b схемы рис. 1.23 не

подтекает. Поэтому если в формуле (l.lfi) принять / = 0, то из нее может быть найдено напряжение Vot между двумя узлами:

I 2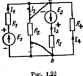

(1.20)

После определения напряжения U находят ток в любой (н)

Ом и К,-10 Ом. Решение.

0.5+0.25+1+0.1 1

=67.3 А;

, = й=. = °=М-,135А; ;, 56,4 А; /.=-0.64 А.

В схеме потребляется мощность

т,+SR..+IR,+т. - 67.3= 2+

+1.35.4+65.4 -1+0.64

i 10 = 9647 Вт.

Источники Э.Д.С. доставляют мощность Exii-Eth + 60 55,4 = 9647 Вт.

=120-57

1-57,

Q 1.22. Метод узловых потенциалив. lu-v в -i,.. -.....

Moluo найти по закону Ома для участка цен , содержащего Э.Д.С.

Ток в любой ветви,<:хемы

Для того чтобы можно было применить закон Ома, необкодимо знать пшенцпалы узлов схемы. Метод расчета электрических цепей, в котором за ненавесшые принимают потенциалы узлов схемы, называют методом узловых потенциалов.

Допустим, что в схеме п узлов. Так как любая (одна) точка схемы может быть заземлена без взыеиеиия токораспределения всхеме, то один из узлов схемы можно мысде1шо заземлить, т. е. принять потенциал его равным нулю. Пра этом число неизвестных уменьшается с n до п- I.

Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа. А5етод узлоылх потенциалов, как и м<ггод контурных токов, - один из основных расчетных приемов. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономичным, чем метод контурных тотов.

Обратимся к схеме рис. 1.24. которая имеет довольно большое число ветвей (l)нq)aвнитeлыo небольшое число узлов (4). Если узел 4 мысленно заземлить, т. е. принять (f4 = 0, то необходимо определить псп-енцналы только трех узлов: (fj, ц/, Гя. Для единообразия в обозначениях услЬвнмся в § 1.22 токи писать с двумя ицдексамп: первый индекс соответствует номеру узла, от которого ток утекает, второй индекс -noMqjy узла, к которому ток подтекает. Проводимости вегвей также будем снабжать двумя инджсами. Необходимо заметить, что эти проводимости не имеют ничего общего с входньши н взаимными гд)Сиод11мостями ветвей, которые рассматрива-днсьв§ 1.15.

В соответствии с обозначениями токов на рис. 1.24 составим уравнение по левому закону Кирхгофа для первого узла:

Пг-г +- 1U+-и =о,

[El, - (ф, - Ч).)] gl, - {E ~ (q - n)]gl, -f

+10-{т-9.)Ы-1Е-(-ч)Ы*+ +[£.-(Ф.-ч)1й +(£ -(<Р1-Ф )1е..=в.

Перепишем последнее уравнение следунщим образом:

<P.Cu-f<p.G -bq>3Gia = / , (1.21)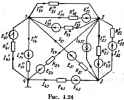

Gtt=~ig +gn+g:: G =-g : / = Ei + Е,ф, + E g;. ~ EUgl, - E, .

Обсудим структуру 1фавнения (I.2I). Множителем при в нем является коэффициент d,. равн1Ж сумме проводимосгей всех ветвей, сходящихся в первом узле. Проводимость G, равняется сумме проводимосгей всех ветвей, соединяющих узел / с узлом 2, взятой со знаком минус. Аналогично, С,з есть сумма проводимосгей всех ветвей, соединяющих узел / с узлом 3, взятая со знаком минус. Ток / , называемый узловым током первого узла, -это расдетная величина, равная алгебраической сумме тсжов, патученных от деления э. д. с, вегвей, подходящих к узлу на сопротивления данных вегеей. В эту сумму со знаком плюс входят тсжн тех ветвей, э. д. с. которых направлены к уз.чу /.

Подобные же уравнения могут быть записаны и для остальных узлов схемы. Если схема имеет п узлов, то ей соответствует а1стема из п-I уравн 1ий вида

ViGn+4>tGi2+:. + Фя-А! - /ц:

(1.22)

где CfcR -сумма проводамоетей ветвей, стодяшлхся в узле fr. - сумма цроводимостей ветвей, соединяющих узлы кит, взятая со знаком минус; -узловой ток А-узла. 1-:слн к А-узлу подтекает ток от источника тока, то он должен быть включен в ток со знаком плюс, если ут £ает, .то со знаком минус.

Если между какими-либо двумя узлами нет ветви, то соответствующая провсйнмость равна нулю. После решения системы (1.22) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего э. д. с.

Максвеллом было установлено, что распределение токов п электрической цепи всегда происходит так, что хеиловая фупицня системы

АГ-1.г.З.... =1.2,3....

ыннннальна.

Коэффициент >/а обусловлен тем, что ври двоЗном суммировании мощяосп каждой вегни.учитывается дваады.

Доказательство основано на том, что совжуиность уравнений (1-22) рвляется JBoiHocTbio условяй минимума функция Р, т. е. совокупностью условий д1 = - V=® - производные у.=Cii>0.

2 Л- ииюжителысы. то. дейстеигельио, это есть условии ннн

мука тепловой функции.