Принимают, что при х=1 /СОЗ ! = 1/(2, откуда т=. Шяагая р=/ж,

Прв ямбпкях я

прн четных ;

j.-im-eW . 0.1.....

pj-C-ljIM-e . *-0. 1. .. .

(мфужности едяннчнот радиуса, тъ Kiljfi н шываютс! I Баттерворса. Лрн с>к.-т1 используют значения pt, > щиесй только в левой я. Это обеспечивает есуществмюсть КЩ.- линошпри в=1. 2. а прв я=1 + при я=2 ffl+y2p+. при й=3 /Р+2яЧ-Задзваясь вепичнноП ого -затухания фильтра в белак (обычно при x=S] = iOlg((/i/*. определим гк

20lg2

Например, при о=18дБ л=18/(20 lg2) =2,98= 3. В ,

=р.+2р*+2,-Ы-о К (р) реализуют известными методами. .новая tampckcumtoffui. Полиномы Чейлвевв порядка л

Полагав Brccosx=6 и имея в нкду.

Xsin**-!-... , а sine=Kl-получим алгеОмнческую форму аапвся i номов:

Г {х) =* +С]1- (ж -1)+С4* -* (* -1)1+ ...

Например, при/1=5 Ть{х)=\Ь)?-20з?-{-Ьх. В яитемале 1=0.1 Tb(j юлеблетс* от jr> I Т Щ иототонно Bcepamer.

1 до -I (рис. 10.11. а I функонн фильтра НЧ

Максяжальное отклотенв* \КЩ\ от 1 равно W2;

, х> 1. т. е. в еблаетн satjmuhbx фаиьтра НЧ,

Примерный ввд аппровснннругащй кривой lf (jx) показан на рнс. 10.,11.в. Для аадашосо опишнеиая f н величины аатухднна а s децибелах лри х=2 lg\UxlUt\=iliti{UK{fl)\ порядок полишжа Чебыиква онреиеляют по

формуле

где 1.32=.АгсЬ2.

Например, для 7=0,4 и о=30дБ при х=2

Для сштавшию следуй яределить шжсы *С(М1.

л ой потшлоекосте. Пеогташ в IK(/4I прнрав!

у f/f (/*>! !

айакенатедь

При 0=ех1 г,(4=r,(ш=-cosn[иccos-aJ=±-L. При ж>1 r.(x)=r.(j=.dinArch-. Таи ш1ж р -кюшдехсме ксдо, то arccoS которое полоишн равный cCjt4-/pA- Тогда

приравняем к вулю

тоже KOHiuKscHoe кло,

r (=ce8( a*+/i#j)=eoaB *chep -/Bin/ia*sh pft=± v. Отсюда

cosBaich/ipt=aff к йпяв4яЬвр=а±:1/у. екйРьО, то

сов/Ю4=0 н ав=+1)-я/(2 ), *=0. I. ..., в.

Так

При этом

йппаА=±1; sh Pft=l/TK p*=Arsbl/v. Поскольку вгссав(р /;)=аА+/Рд, то

Pfc=ал+/Ь* => / cos (aj,+/р ). Действительные н мнимые части полюсов р*, лежащихвлетой полуплоснестн:

Иэ Последнее строчки следует, -ио

е- полюсы pfc расположены на эллипсе, одна полуось которото равна shp , другая-ch рц.

сьрРуРвваеши примере при 11=4 и р*=0,412. shp4=0,42l;

Для построения эллипса чертим две окружности одну раднусшв $h тую рядиусои dl Pft (рис. 10.12) н через начало координат проводин i- пересечения с окружностями под углами а4=(2А+1)(я/2п), где k=

В примере а 22.3; 67; 111; 156 .

Из точек пересечения лучей с окружностью меньшего радвус! тикали а из точек пересечения с окружностью вольт

Точки пересечения соответствующих горизонтален н

плоскости дают искомые полюсы. В примере р д=-0.164.±/0.9№; , = -0.388±/0,41б. Нормироваиязя переда

(Р-Р,) (Р-Рс) (Р-Р.) (Р-Р,) 1(р+0.164) +0.99№1ИН(

По /С (р) определяют схему i хода от нормированных к действ июнкянн L=LJv>c и С=С 11й( .

Какому спосЛу синтеза сх предаочтйше, :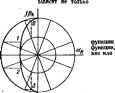

е нормированные параметры 1. Сд. Для й ельным параметрам L, С пользуются

ны и какой конкретной схеме следует v от стоимости и от габаритов при и осуществлении схемы, но и от то ко фазочастотные характеристики г ся четырехполюсников удо левной задаче.

В заключени распространяется

ia. Св Я частота

X). к I Z. а t

Еслн аппроксимируют функцию, а входное сопроп сть) некоторого двухполюсника, то оно о нормируется не только но частоте Юд, но величине. При нормировании Zip) по wJ не входное сопротивление (прсжоданость) щ на некоторую безразмерную величину НщЛ При перетде от схемы, реализунтй im рованное сопротивление Z (ее параметры J ; шнормировшиалми t

leHHo сопоставив почленно одинаковые слагаемые у р-=-р- Получим к=ВЛ Ь=Ла(-).С-адйвШв): а,-велн

1. Определите задачи синтеза, переяпслите условия, которым должны летворять Z(p) физическв реализуемых дтхпслюсииков. 2. Поясингте цдею лизацни двухполюсников леешичной схемой. Покажите, как следует упо оЕфеделятъ ее нлементы. Любое ли Z (р) может быть реалвзовано л схемой? 3. Как оществнть

четырехполюсник называют микныапьиофазсвым? 6. Запишите условия в условие ннирственной части для Z-параметров. 7. В чем состоит задача i симации и как она решается? 8. Как от нормированных параметров neJ к ненормитжаиныы. задавшись некоторыми RoKin 9. Решить задачи V2,.Zi\

ГЛАВА ОДИННАДЦАТАЯ

УСТАНОВИВШИЕСЯ ПЮЦЕССЫ В ЭЛЕКТРИЧЕСКИХ Н МАГНИТНЫХ lUnflX, СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЮНМИ ПАРАМЕТРАМИ

§ 11.1. Основные определения. В данной главе расхмярены основы теории усташжившихся процессов в элестрических и магнитных цепях, содержаищх линии с распределашыми параметрами.

Эжктрическшли линиями с распределенными параметрами называют такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к Другой, соседней точке.

Под маеяштшми линиями с раагредеяениыми параметрами понимают такие линии, магнитный пйок и магнитное напряжение вдоль которых непрерывно меняются при переходе от оддаой точки линии к соседней.

Эффект непрерывного изменения тока (потока) и электрического (магнитного) напряжения вдоль линии имеет место вследствие того, что линии обладают раофсделашымй продольными и поперечными соиротявленняш (рис. 11.1, с).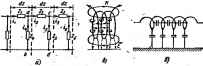

На схеме рис. 11.1. а изображен участок линия с распределенными параметрами, через dx обозначен бесконечно малый элемент длины линии.

Сопротивления Zs, Zg, .\. называют продолышми сопротивлениями, в иих включены сопротивления и прямого, и обратного проводов; сопротивления Z, Z, Zg, ... называют поперечными сопротивлениями,

В результате утечки тока через сопротивлеяне Z ток /a i. Аналогично, ток цФН и т. д. Напряжение между точками о и Ь ие равно напряжению между точками с и d и т. д.

В электрических линиях с распределетными параметрами продольные сопротивления образованы активными сопрагавлениями проводов линии и [шдуктивносгями двух противостоящих друг другу участков пинии длиной dx. Поперечные сопротивления состоят из сопротивлений утечки, появляющейся вследствне несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг

10 Зав. 1658 289

другу Элементами (участками) линии. В магнитных штяз с } пределенншш параметрами продольные сшроЕШЛШмя преост собой магнитные сопротивления самих магнитных сте1вкней, о щих магнитную линию, а поперечные соаротивлення обус*. , утечкой магнитного потока по воздуху между противостоя! другу участкаш линии.

Линию с распределенными параметрами назывгвог однородной. равны друг другу все продольные сооротивления участке одмнакобой длины и еслн равны друг другу все поперечные с тивления участков линии одинаковой длины. Так, участок рнс. ПЛ. а однороден, если Z, = Z, = Z,= ... и 24=.Z =Ze.

Линию с распределенными параметрами назьшают неодио>~-ш если продольные сопропшлення в ней различны или сопропшлення неовниаковы.

Кроме того, линии с раофеделеияьши параметрам можш разделить на две большие группы: нелинейные и линейние.

В нелинейных линиях е рас1Ч)еделенн1 и пгааш1ра*й про л н (или) пшеретшле сшрошвлашя являются фикциями iijkti i по ним тжов, в линейных продольные и n iep onje с не являются функциями протекающих через них тсжов.

В качестве примера нелинейной электрической линии с j ленными параметрами можно назвать алектрнческую линию i высок01-0 напряжения прн наличии между проводами линии электрического разряда -явлаше короны на проводад, В этом t чве емкость между протавостояиншк друг другу участками является функцией напряжения меяд© этими участкгми.

В качестве примера нелинейной магннтнсй линии с распрев ными параметрами можно нажать линию, образованную параллелЛ расположеншлда MarHHTHbiMtr сердечниками, которые в процессе р линии могут наыщагься.

Когда говорят о линии fe распределенными параметрами, то о этот термин мысленно связьшают с метЦными линиями передачи тритеской энергии на большие расстояния, с телефонными нт ныш1 воздушными и кабельными дцниями, с рельсшыын , автоблокировки на железнодорожном транспсрте, с ангатнамь диотехнике и другими родственными линиями и установками.

В то же время с линиями с распределенными вармлетрами дело и тогда, когда линий в буквальжш смысле сжжа, казалось й вовсе нет. Так, обычная нцдукшвная катушка при достаточно ких частотах представляет собой лииию с распределитымн i рами. Картина электрического и магнитнио полей катушки i на рнс. 11.1,6. Линнн напряженности электрического поля £ i заны пунктиром, лннаи напряжеиности магнитнсго вол Й-сг ными ляиняк .

Схема замещения катушкв гожазаиа на рие-. ПЛ,в. Из i ввдно, что кроне гащуктвиосгей в схеме есть межвитковые < и емкости на корпус прибора (на землю.

Если по катушке гфоходат перемятый ток. то вдрез i вш анюств и шкости на землю также вдет ток. однсм (

j e напряжении между соседними витками ток через емкости тем 6о.чьше. чш выше частота перемиштэ тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоиэтлеримо мал по сравнению с тсжами чфез ви ши катушки и наличие емкостей можно ре ущпывать в расчете (что и делалось до сих нор). Если же частота тока очень велика, например сотни миллиардов тщх, то токи через емкости могут во много раз -претышать токи через витки катушки, g этом случае вся катушка в челом-будет оказывать прохождению переменного тока емкостное, в ие индуктивное сопротивление (коли-чеавенные изменения вдзсшяи в качесгветные). Гж промежуточных частотах порддка нескольких мегагц (когда линейные размеры катушки соизмеримы с длиной волны) индуктивная катушка является типичной линией с распределенными параметрами. Еслн индуктивная кат>шка намотана на стальной сердечник, который споссйен насыщаться и частота тсжа достаточно велика, то все устройстаэ в целом представляет собой сложную совокупность из элаарнческой н магнитной нелдаейных цшей с рашределсямшн параметрами.

В курсе ТОЭ изучают только основы однородных линетных цшей с распределенными параметрами. Вся теория излагается применительно к электрическим лишям с распредеденнмии парамефэми на переменном токе. Теория однородных .чинейных электрических цепей с распределенными параметрами на постоянном токе ннюсреппвенно следует нз теории цепей псременнсто тока, если принять угловую частоту равной нулю.

Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с расцределетными параметрами, только вместо тока в уравнении должен быть подставлен магнитный поток, вместо электрического напряжения - магнитное напряжение, вместо продольного активного сопротивления - продольное магнитное сопротивление, вместо поперечной электрической проводимости -попд)ечная магнитная проводимость.

§ 11.2. Составление дифференциальных >фавненнЯ для однородной линии с распределенными параметрами. Пусть /?( -продольное активное сопротивление адиницы длины линии; Ьо~ч лукттаость

единицы длины линии; Q -емкость единицы длины линии; Со- поперечная -проводимость единицы длины линии. Поперечная проводимость Go не является сратной величиной продольного сопротивления Bj,.

Разобьем линию на участки длиной dx {рас. 11.2), где х-расстояние, отсчитываемое ог начала линии. На длине dx активное еопротивление равно Radx, индуктивность-Z-odj:, проводимость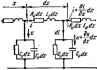

Рис. I