Модуле этая Шфсадатрчных функций оятвкош В равны p;if, i аргу №нты различны. Аргумент цч-фа первого чета меята ф;-чр, второго четырехполюсника. Четыреяг

В м. ф. четырех!! существует одпоигачи; мость меаду модулем и аЛ той передатпшсЛ функш и. ф. четырехполюсниках и модулем н аргументом imL точной функции нет ЩлЛ ноВ

* физически ocymecTBi:

i илв по г- млн У-пара еграи.

Рассмотрим вопросов, которые оов-четырешолюсник по з

§ 10.7. Условия, i

етры ч

юточнуш функцию. Перед тем как paocMoipeib совокупность Boapocos, квпоиннм основные уравнения линейного пассивного четырёхпс в Z- н в К4орме.

Уравнения четыреяполюсвика в Zopwe:

Симы для рнс. iO.7. а, б; Ец-

аределення Z , г .

изображены <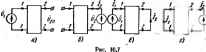

Zu-входное сопротивление четырехполюсника во

при раэомкнутыл зажимах t-J (в $ 4.2 обозначалось 2 ): Z -взаимное с тнвлеине между входной н выходной ветвями. Для схемы рнс- 10.7, а

X 2-2 C ==UZ. На оснайния теоремы Уравнения четырехполилннка в V-форме:

Схемы для рис.. 10.7. у, е; Гц -i

о к зажимам 2-2 прн ксрроткоэаМ1и1утых зажимах /-/. Лежду Z- и У параметрами существуют соотношения:

Если вычеты фднкцнн Z. 2ц в рассматриваемом полюсе оОоэНачвт*

соогеетствипю ки *ц> то любом полюсе вв оси / межлу вычетами имеет иесто соотношение

Т * *и-*г,Э:0, (10.I2J

которое называют условием вычетов. Доказательство этого условия производят методами матричной алгебры; в силу громоядкопи оно здесь пе дано (см., иапри-иер. [9]). Условие (10.12) означает, что матрица вычетов Z-iapanerpcB в полюсах является неотрицательной. Для !-параметров условие (10.12) такженмеет -ГИЛУ, причем лсд Ац, *м *is * случае следует понимать соответстапю гы в полюсах функций Гц, н У ва оси

Заметит, что если в полюсе выполняется условие Ли-*} =0, то полюс называют компохтиыя. Z- вли У-параметры, во всех полюсах которых выполняется условие компактности, называют компактными Z- или У-параметрами.

Входные сотротивления четырехпаяюсннка со стороны зажимов /-/ при X. нли . 8. со стороны важимов 2-2. а также входные сопротивления со стороны Зажимов 2-2 при i. х. нлн к. я. со стороны эажвмов /-/ должкм удовлетворять тем же условиям, что н входные сопротивления двуклолюсншии

роме того. Z-параметры любого четырехполюсника на любой частоте и(р=(и) должны удовлетворять еще так иазывянгому условию ваиествошой части (условию Геверца):

(10.13)

где r =ReZii(/io); Ги=Не2и(;ш); Гц, --ReZ (/ ).

Соотношение (10.13) является следствием того, что матрица пассивного четырехполюсника является положнт л .ипй вещественной. Формулы (10.12) в (1013) накладывают ограничение на коэффициент усиления Q свнтезируемого чешрехполгоснвка. Для Уараметров условие вещественной часта записывается так:

(10.13)

и - Re. У 0 и); gM=Re Ум (i<): £>i = Re Уц (/и)-

3 литературе во синтезу четырехполюсников используют также некоторые I понятая п Теоремы (условия], до сих пор пе упоминавшиеся.

тенным. С прак-11годие урэвнове-

Гознакомямся с основными в

Еслн у входной и выходной ветвей четырехт нет общего зажима, то такие четырехти1югниы1 называ: общий зажнм имеется, то четырехполюсник называют h тнческой точки зрения иеуршнсжешенние четырехполк шенных. так как содержат меньшее число элементов.

Для неуравновешенных четырехполюсников существует условие Фиалкова и Герста. Оно состоит в том. что: а) коэффициенты прн р в числителе и знаменателе функции -У . УиН Ув неотрицательны; С) коэффициенты прн cocnwr-стЕумщнх сгепеиях р в - Уц пе гревишют коэффициентов грн соответствую1дих степенях р в Уц или У. Пря атом предпопагвется, что общий ыножитепь, если си имеется в числителе соответствующей функции, пе софоцается.

При синтезе четырехполюсника задается обычно его передающая функция. Передаточная функция может выть задана различным о(азом. Так, например, она может выть задана в виде передаточной функции по напряжению или току, 4*4 наличии и отсутствии нагрузки па выходе четырехполюсник!, с учетом в без учета входного сотротивления шточника питания н т. п. Довольно часто в Рук(жовств8х но синтезу цепей ее задают в виде передаточной функции по напряжению прн питания со стороны зажимов /-/ и х. х. на зажинах 2-2

рис. Ш.7, а).

Будем ее обозначать К ,лЫ=<ях.х литературе расяространеио обоэна-ченне Г,:

( >,.=Г =1/ /11=г К =~У,Уи. Полюсы Кв11 оС51аэуются иа нуле Zu. которые ве являются одновременно Улаын Za. Л иа полюсов Zu. пе являнхоихсв однс реыеиш) полюсами Zi,.

Передаточную нкцню к хл ожво представк . в вцде отвошемия t полвяомов по степеням р:

г 0лР + Дп-1Р +-+О1Р+О0

Есл вынести за скобки а в чисяятеяе я Ь, в зувменателе, то пояушн

т Л

Отношение ajb обозначают k (или Q) я

Как уже говорнлось. прн решетш задач синтеза четьфехполюсмиков неа дямо Знать свойства Киы составляющих Zu, или - У]я н Уи-рые них были сформлировякы в настоящем параграфе. Дополним их к др;т : менее важными, опуская доказательства. (Доказательства можно найти к .

перечислены важные для Ыккза своВства Zn. Zjj которые должны быть выполнены для любого четырехполюсника. В ш рассмотрены те донолнкгелыпл свойства, которыми обладают частн! четырехполюсников-

I. Условия, накладываемые на Zu. Z. У , У , дм всех п

.. Должно быть ;

условие вычетов я условие вещее части.

Б. Условия, лготорые должны выполняться в полюсах функций:

I) полюсы Zia. У,я и Кик.х могут находиться в правой полушюжостщ-

У fifx.x не может бьт, пелюса в нуле в в брсконечности;

3) полюсы Zia и Уи оси /и-простые с вещественными значення вычетов;

4) полюсы квк.ж на оси /ш-простые с мнимыми вычетами.

Б. Условня,-когорые выполняются в отношения нулей функций: нули Zu. К 1л Могут Сыть кратными в находиться в любой точке плоскости р.

II. Передаточная функция Килл неуравножшеяяого четьфоаюлюашка таамноП индуктивности обладает сдюиши свойствами:

1) ее нули могут находиться на комплексяой плоскости всюду, кроме 1И жителыгой вещеовсзпюй оси;

2) при положительных ввцествеяных р величина передаточн!* функция а дится между О в 1:

3) и4Юф1} щненты числителя передаточной функции положительны (часть них может равняться нулю) п не превышают соогветста1тошлх коэфжци - знаменателя при условии, что функцию не сокращают на о№№Й множитель.

т.сеогкт

I) нули передзточ

могут находиться в любсЛ точке клм) плоскости, включая и полдаительную вещественную ось;

2) для положительных вещественных р величина передаточной

находятся в пределах -Крайние значеяиг-------------------

р=0, илв при р=со, или в обоих этвх случаях;

I можно получить только <

3) коэффициенты в числителе передаточной функции могут быть огряц иыми. ие превышая но величине соотвиствующие коэффициенты внаметател! условий, что функцию не сокращают на общий мисжтель.

Частным видом четырехполюсника с общим звжвмои (неураввовеше! является цепная схема,

IV. Передаточная функция цепных схем обладает дополнительным своОст се нули не могут иахадитьск и nptiiwfi нояоскости.

V. В еще более частном случае-в случее цепной схемы, собранной г

только иа с

Для цепных ТС-четырехполюсвиков нули н полюсы являются простыни, расположены на отрицательной вещественной оси в чередуются. Полюсы Уц располагаются иа отрицательной вещественной оси и являются простым Нули Уы могут быть на отрицательной вещественной осн.

Перейдем к вопросу о реализации четырехполюсника по его задав-дой гаредточной функции, полагая, что она удовлеттяег условиям физической реализуемости. Существует много различных мекщоп реа-лизадаи. В одних методах в основу положена пдзедаточная функция при холостом ходе четьфсхполюсннка, в других -передаточная функция четырехполюсника, нагруженного на согласованное активное сопротивление. В последнем случае принято нагрузку брать равной ] Ом и называть ее исмализованной.

В одних методах реализации сшротивлеине источника питания полагают равньш нулю, в друпос-равным заданнсй величине. Каждый с1гособ реализации имеет те или иные ограничения. Так, реализадая реактивных четырех- £т пмюсников методом смещения нуля по заданным

и Yi лестничяЫ* схемой, нагруженаой на к * R, можег &ггь осуществлена, если все нули пе- , Z П редаточной нкцин Кн находятся в левой полу- Т плоскости. 0-1-0

Более общим, но и более сложным являет- in я

ся способ (жализацин по Дарлингтону по трем параметрам 2ц, Z , <2u. ножолякшцй учесть внутрешюе сопротивление источника, а также способ реализации, в основе ког(дюго лежит предстадлеяие пч еп№)чной функции в виде проиэкдавня пдаточных функций нескольких согласованно нагруженных четъфехпошосннкс . Один нз этих чегырехполюсниксе ивляется чегаренкхшосником постоянного затухания, другой -чегарех-полюсником фазового едвига, третий и послелующие-минимально-фазовыми *.

§ ЮЛ. Синтез четъфехполосников Г-образвымн /ГС-схемами.

Г-образный чегьфехполюсннк (рис. 10.8) является делителем напряжения. Его передаточная функция по напряжению при холостом ходе

В дальнейшем вместо Z,lp) н Z,(p) будем писать соответственно

1 К

Положим, что с помощью Г-образного чегьфехполюсника, состоящего из ;?С-элементов, требуется реализовать передаточную функцию по напряжению прн холостом ходе:

VAp)lUi{p)=NlM, (10.15)

где л; и М-полиномы по стигеням р; N/M удовлетворяет услсеияц (а° Р-* ° * мреддаочной функцни /?С-четырех1юлюсннна

-Для

ться к И и [171.

н способами реалязацнн рекстяеядуется обра-

ЕМ правые части (ЮЛо) и

Разделим числитель и знаменатель правой части (10.16) ка н. рый полином Q = Q(p) (не имеет ничего общего с коэффН1ц??л усиления), выбранный таким образом, что он имеет тот же поро что н полиномы N и М, а корин его чередуются с корнями ур инй N = 0 и М = 0. Тогда

Из уравнения (10.17) находим Zt=N/Q н Zi = (M-N)/Q. 1 зуем двухполюсники и 2 по найденным операторным < тивлеяиям*. Реализация двухполюсников прсаЕВсщнтся в соогветст с § 10.3 н 10.4.

Аналогично производится синтез Г-оЕразнымн RL-aieMSm.

§ 10.9.

осник для фаз(№оЙ коррекции. На рнс.

изображена симметричная скрещенная схема, состоящая из >

реактевных двухполюсннкга 1 Za, на выходе которой тлш активное сопротивлааие R. жительные направления токм. i напряжений указаны на схеме, j В уравнении f/a+oZi/l заменим 0 на fR и учтем, что /д = Это дает

выразить It через / :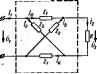

-.fit-

Подставим /, в / =/<>-/ найдем

Составим уравнение для периферийного контура: Передача напряжения

Входной ток

Предполагаем, что полином Qip) может бшь ьаВден в что Zi н Z, yl летБоряют услшияы, перечислшиш в § 10.2.

Входное ссяфотивлпше

/, 2 +Zi+Z, *

Приравняв Z = R. получим соотношение Z,2j=J?\ Из него следует, что реактивные сопротивления Zi и Zj взаимно статны. В формулу для Ки подставим Za = R/Zi:

<и=--Ки( >)е>п->. (а)

Так как Zj-чисто реактивное сопротивление, то модули числи-дая и знаменателя формулы (а) одинаковы и потому Kv = 1- При изменении частоты ю меняется только аргумент q>(u>). Четырехполюсник рте. 10.9 служит для фазовой коррекции. С этой целью его включают между источником тштания с внутренним ссяфотнвлетим* R и активной нагрузкой R, и он, не изменяя -напряжение источника литания по модулю, поворачивает его на требуемый угол ф((о) по фазе, осуществляя этим фазовую коррекцию. Определим Zj из (а) при нормиротанноб нагрузке R=l Ом:

По известному Ки(р) найдем операторные сопротивления zp) i zap) и реалием-их методами, рассмотренными в § 10.3-10.5.

которая точно совпадает с заданной нее в допустимых пределах вне STHX точек, давая в то же время физически реализуемую фу1

Аппроксимация-это пря-

я другой частотной зависимостью.

о фнльтра FC{/*)-ne-

Рис. 10.10

l4f&i)l=/(*). гдеКО. Радаточная функаня; х = е)/щ; с-безразмерная величина, равная частоте среза. , В диапазоне изменения jc от О до

Пункти{1ная кривая t рис. 10.10, б повторяет кривую рис. 10.10, а, кривая 2 характеризует гладкую аппрда-имацню. прн которой отклонение от кривой 1 неодинаково в диапазоне аппрок-№йацнн Кривая 3 иллюстрирует равноволиовую аппрсжсиыацию, при которой абсолютные яначения каксшалышх отклонений от кривой / в обе стороны qw- аковы. Гладкую аппроксимацию осушествляюг обычно полинокамв Батгерворса, равноволиовую-полиномами Чебышева (Кривые 2, 3 рис. 10.10, б неточны).

Гаадкая аппроксимация. Применительно к фильтру НЧ анпроюжнацкю квад-Р а модуля ич)едаточно11 фупквди ч----------------- --------------

а оществляют т.