Кдаффиштента в выражвши

отределяюгкаки

вычет функции Z(p} в полюсе рщ [&лу же ржш вычет Z(p} и р= -/Шй, так как они ta действительны]:

После того как яацдено оа можно определить I-ft и С даух я люсника рис, 1а2, е:

. С*=1/(2й,); La=1/(o)Q.

Реализацию двухполюсника можно осуществлять не только по входаыу сопротивлению Z(p), но и по его входной нрсшодим Y (p)=l/Z(p). Входную проводимость Y(p) 1федставляют в ввде рис. юл 6

в соответствии с правой частью (10.4) двухполюсник о . в ввде параллельного соединения шкости ai, индуктивности двуя шлюсников по типу рнс. 10.2. а (им соответствуют слагаемые i

-j и двухполюсника минимальной реактивной прсводимссги 1

не содержащего полюсов на мнимой оси. Коэффициенты и с деляют путем нахонуйэшя интегральных вычетов функции Y{p) ( ветственно при р=0 и р = /ю , а С=л;= Нт Y(р)/р.

Если функции реализуют в ввде г

ного соединения двухпогаоашксш рис. 10.2, е. Если функция Y(p) -== реализуют параллельншй соедиветием двухполюсник

рис. 10.2, ж*. Следует иметь в виду, что, при реализации дв люсника по его Z(p) в ввде последовательного соединения проск двухполюсников, начиная с некотсфого этапа, может сжазаться i сообразным перейти от сопротивления к прсеоднмосга и j реализацию осуществлять уже паллельно соединенными двухпол. никами. Потребность в таком переходе может воямкнуть, яапрн .с когда остающаяся для реалиции часть Z(p) имеет нуль при р - щ Этому нулю соответствует полюс Y(p) при р==0, который реали-а индуктивностью.

Пример 114. Реализовать Z(p) = ±.

Решение. Так как Z(p) имеет полюс прн р=0, то в схеме к жет быть выделена послешжагелыю включенная емкость С= i iie==ResZ(p)==2/2 = l. Счгнкция Z(b) не имеег полюсов, , р=о

на мнимой оси. Поэтому в состав его не входят последовательно ида Л * Полагаем, что игаффициенш тяг действительны и положительны.

ченные явукполюсннки типа рис. 10.2, е. Определим, кмме Z{p) осталась рсглизотать {нашвем его Z,(p)I:

Функция Zalp) имеет нуль прн р = 0. Для ретлизашн оставцкйся части схемы перейдем к проводимости Уя(р)- Полюсу этой проводимости прн р==0 соответствует индуктивность aiResKaO)!.

р = 0

Осталось реалйзсшать

Слагаемому р/(р4-2) в соотвегсгвии с рис. 10.2, ж отвечает ветвь из последсщательно соеданеняых ?= I Ом и С=0,5 Ф. В соответствии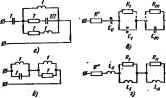

срис. 10.2, е проводимости 1/(р4-2)огвечаетве1вьс1 = Полученная схема изображена на рис. 10.4, а.

1 Гн7? = 20м,

Пример 5. Реализовать Z{p)= ffJi-

Решение. Прн р = О у Z (р) нет полюса, поэтому последовательная емкость у искомого даухшмюсяйка отсутствует. Функция Z (р) имеет два полюса Ри=г1:/, распож)Жй!иых иа Зримой осн. Выделим параллельный резонансный всжтур рис. 10.2, в, соотаетсгвующнй этим полюсам:

Сй=1/2а*=1Ф; о*=1; U= l/(MjCft)= 1 Г. Найдем функцию мнннмалыюго реактивного сопротивления:

в coonseiCTBHH с рнс, 10.2. г реализуй в виде i .

ГЮГО соеяиншия активного сопротавления 1 Ом и индукгнвноста Схема искомого двухполюсника изображена на рис. 10.4, б.

Двухполюсники, состоящие только из и С, могут быть I аованы, например, кансническс схемой рис. 10.4, в, а состоящие и £ -схемой рис. 10.4, г.

Для схемы рнс. 10.4, в

+ ..-i: d.=:

R= Пт Z{p); at,=-livipZ(py, bk= Res Z(p). Для схемы рис, 10.4, г

Zip)R+pL.+ 2; ,

= lim Z (ру, L =nmZ (p)/p.

Параметры Rk и Lj, находим, имея p соотвегсгвует паллельному tnj.=RtfU Res Z(p)/p.

4. Если частота, n

[ум ReZ(/(u). p

виду, что I

Rk h 1де с

% 10.5. Метод уне. Основные этапы метода Бруне с 1. Прежде всего проверяют, не соджит ли заданное Z{p) [hi вш его Z.M (р)] полюсов на мнимой оси. Если они имеются, тс состава Z j,(p) выделяют соответствующие этим полюсам один весколько посждажателыю включенных параллельных резона! контуров. В результате получают

Эют этап соответствует пфеходу от рнс. 10.5, а к рис. 10151 Коэффициент flA== Res Za (p). 1

Функция Z{p) ие имеет полюсов на мнимсда оси и представ. собой функцию минимального реактавного сопротивления.

2. Полагая р = в Z(/cp) выделяют детствигельную часть, т.1 находят ReZ(/co) и определяют частоту ю, при которой ReZ(/e)).i нимальна. Эта частота может быть равна нулю, бесконечности к иметь некоторое конечное значение (в последнем случае ее будем i. зывать Юо)- Йодсчита также минимальное значение ReZ(yGi), кл рое назовем R i .

3. Из Z(p) вычитают 7? , и находит Z,(p). Этой операции вегствует переход от рис. 10.5, б к рис. 10.5, е. Заметим, что пени числителя и знаменателя одинаковы.

тглю или беосонечноста, то уже на этой стадии делается попытка реализовать Z(p) лестничной схаюй, Еслн же минимум ReZf/ra) имеет место при некоторой *о==Ю(, отличающейся от О и оо, то дальнейшую реализацию пронждят всоответствии с п. 5-12.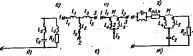

5. Подсчитывают Z,(;j) при р=/Ч- Так как при частоте р=;о)в действительная часть Z(p)=Rmto, то дейстшпельная часть разности

Z(/tii ) -7? 1п равна нулю, т. е, ZAf* представляет собой чисто реактивное сопротивление Zi{jv>-jXf.

6. Возможны два случая. Псавый, когда Xi>0, второй, когда Х,<0. Будем полагать Xi=<a Li>0 (случай Х,<0 рассмотрен в п. 12). Тогда

1=Хщ. (10.6)

7. Составим разность Zipi - pLi и приведа* ее к общвду знаменателю.

Так, иапрнмд), если исходить из того, что

то проводимость оставшейся для реализации части двухполюсника

V / л I ff-fftiP-Hfe,

<>= г,Ы-Ри = -P*i-HP=(l-6iiJ-HPte-ft.tj+a.-

Обратам внимание на то, что в знаменателе Уо(;) имеется слагаемое-pV,i, которое при далмейшЫ! реализации приведет к появлению в схеме отрицательной индуктиыюстн.

8. Поскольку при р = 1Щ Zi(p)-pLi=0, то Yc(p) = oo. т. е. Р=/Оп является полюсом У(рУ Наличие полюса у Yo(p) позволяет представить оставшуюся часть двухполюсника аегаью из последажй- ьно соеддаенвых и С, настроенной в резонанс на -частоту йд, и параллельно ей присоединенного даухполюсинка с сопротявлагием

г. (рнс ie.5. ф

PIL,

9. Полагаем Zt{p)=N{p)/Ms(p). Степени полиномов Nlj Mi(p) должны быть такилш, чтхйы после приведения правой (10.7) к общему знаменателю, степень полинома числителя левой ч равнялась степени полинома чнслит&ля правой части; то же и в шеинв степеней знаменателей. Так, если Ув(Р) сошвегствуег выл* ПИЮ ( ), то Z, (р) = (с,р + сЛ*.

Методом неопрепрлеиных коэффиниентов можно найти Cj, Cot-del Lj. В рассматрввае.чом случае

(10.1

Разность (6o -*ie)>-0; это следует из того, что условие Х:: означает, что l ,[gg±]>0, а при р=/ш ReZ.(p)=ft

10. Реализацию Zip) npoHSaojWT, как правило, лестничнойсхв*т1 Так, в рассматриваемом примере Zip) реализуют нцпуктавнчти L3 = cjdo = ~e&ilbo и активным сшротивлеяншУ?з==йв/&о (рис 10.5, Важно оатжгь шпплакйе на то. что 1 сжазалась огрицателадой.

1 \. Так кш. физически осуществить отрицательщю ивдукч - нташможно, то далы1ебшнй этап реализации в методе Бруие с:с в том, чтобы три магнитно не связанные ицдуктаыюста Z, Lj, i заменить трансформатсмял, состшищм из индукишносий и меяод которыми имеется магнитная связь (взаимная индуктавностъ Это дйкпвие является обратным по отношению к операции швания магнитносвязанных цепей.

На рис. 10.5, е изображены два участка цепи: летын до здаавйя, правый -после предбразсшаиия; показгжы псиюжнтет направления токов в ветвях н указаны одноименные зажимы кат1 Напряжения между точкшга t 2 для об(жх участков цепи в их эквивалштности должны быть одинаковы, т. е.

Подставляя в эти дае строки /i = /e + /8 и учитывая, что ваиед- из уравнений должно ущжлетворяться при любых жачошях i получаем:

где Li и и положительйы. Окончшельная схема изображена i рнс. 10.5, ж.

12. Если условиться сумму степеней полиишюв в числителе и i мевателе Zs (p) называть гаядком Zip), то совокупность i числашых операций ( цикл Бруне ) поадоляет снизить порядок i Естественно, что потреость в каком-Ж1бо- одном илн; ------

этапах в яобсял кипфетном пртмере ьгожег н т возникнуть (яапри-ffgp, в этапах 1 или 31.

Для ZipX порядок которых достаточно высок, может возникнуть потребность нрйменнть эту последатательностъ операций не один раз. В истечение заметим, что если в п. 5 Х,<0, то /-i<0, я вычйтанне согласно п. 7 сопротивлетия - pIZJ сводится к прибавлению сопротивления +p\Li\.

Некоторым недостатком метода Бруне является его относительная сложность а иаобищнмость введения в схему -ндеальвого трансформатора с коэфйщиентш! связи K=-Ml(LiLb)=l.

§ 10.6. Понятие ом

..дх. Из § 8.64 известно, что передаточная функция четырехполюсника К (р) равна отношенню опцитсфиого вэоСраженин выходной величины к оптеому изображению вхщдаоЙ. Ее можно представить и ввде отношения двух *10лино*юв.

Полюса К (р) всегда находятся в левой части плоскости р. в самой общем случае часть нулеП К (р) может находиться и в правой части плоскостн р. В соответствии с рааюложеяиен Л¥леП 1ге5)едаточной икн все четырехполюсники можно подраэдЕЛИТь Ив два клвсса: на минимально- и наовпшально-фазовые.

Мияимвтно-фазовьчли (м. ф.) ивзывают такие четырехполюсники, все яуяя передаточной нкции которых расположены в левой части плоскости р. У тяи-намалыт-фазовых (н. ф.) четырехполюсников хотя бы часть нулей ташздится Б правой части плоскости р.

Название объясняется тем, что при одинаковом значении модуЛ!

вой функции ы. ф. и п. ф. четырехполюсников четырехполюсника ьше фзы передаиг-

передаточной функции м. ф. йй . ф. чешрехнашоеннка. я знаменатель лередв вч-

Поясннм сквзаниое. С эий адалыо 4>азложим иой функции на ыиожителн:

ь-fni (Р-Р>> <Р-Pi) - iP-Pn)

где pj, pt, .... р -нули, а р, р.. -. Рт-полюсы передаточной фунжюш. И нули и полюсы в общем случае npesciaBjraKfr собой комплекс * чнсла.

Если исследуется работа четырехполюсника в установившемся сннусондаль-ном процессе прн изменяющейся частоте ш, то вместо ръ К{р) поставляют /ш. Каждый ка биномов р-рп ножнб представить в показательной форме в виде Ple\ где pj-модуль, а qij-аргумент комплекса р-р*. Угол грц огсчитъщается ог оси 1 ксяиплекымй плоскости в направлении против часовой стрелки до полоиштельного направления вектора p-Pk- С учетом сказанного

шя для дэух fiepeiTO4HUX фушзлб:

Р-Рш

JCipy

Положвн, что pi ti р 1>авиы по модулю и дствигежпы. Нуль перв-вго выражения ваходвтся в ттЛ частя пл(ккоста р (рис. К£, а), а нуль второго Р=-р[-и правой части ялогаоспс р (рнс. Ю.Б, 6j. Пусть на вход обшх четырехполюсникот возлейстбует свп:сядалы1ое напряжение частотой на. Некоторой конкретной частоте на ксмплексной плоскости соответствует точка а ш оси +/ Образуем разности р-р± я р-р нз рис. 10.6, в н разности р-р, и р-р% Иа рис. 10.6, б:

Р-Р. Pi P~Pt PI