происходит при /7-1оо, можно считать происходящим яа мнимой . плоскости р (мнимая ось простирается в бесконечность). Но тона мнимой оси получается кратный корень, чего быть ие может.

Проведя такое же рассуждение для дуального двукполюа убедимся, чго степень а не можег быть больше степени т ( чем на ].

ЕсЛи в Z(p) вместо р подставить /ш, то Z(/<u) будег предсгавли- , собой компдй(сное сопрогавление двухполюсника в усгановившшог сииусовдалыюм режиме прн частоте , а ReZ(/o)) -действительн\ . часть входного сопротивления. В тсяи случае, котда двухж содержит активные сопротивления, его Re Z (/{ )> О [он поп активную мощность /ReZ(/u))]. Если же двухполюсник чисто реактивный, то ReZ(/<u) = 0. В общем случае для пассивного двухполюсника всегда должно быть ReZ(;to)0.

Пример П1. Задано несколько выражений ввда N{p)/M(p}. Выяснить, могут ли они представлять собой входные сопротивления некоторых двухполюсников:

1) 5£-6 20f+ttip+6 V-HP+t .

Решение. Первое выражение ие моякт представлять собой Z(/ тй( как один из ксэффициигк в .числителе отрицателе!. Второе i третье выражения также ие могут представлять собой Z{p): вто*! потому, что максимальная степень р в знамашгеле больше г - мальнсда степени р числителя на 2, третье потому, что

иях 10 от 0,707 до 1 отрицательно. Четвертое выра;

всем требованиям удовлетворяет и потому может представлять < Z(p) некоторого двухполюсника

Кроме названных общих свойств Z(p) перечислим свойсгеа Z(( двухполюсников, состоящих только из R и С. только нэ R я L t только из £ н с. RC- и 7?1:,-двухполюсники имеют чередукишес простые нули и полюсы на отрицательной вещественион оси плоски стн р. Для JJC-двухполюсников ближайшей особой точкой к нач*л координат является полюс, в бесконечности полюс отсутствует. Г двухполюсников типа RL бтжикк к началу координат особой i мой является нуль, при р = 0 полкс отсутствует. Двухполюснг типа LC имеют чередующиеся простые нули и полюсы на мнимой с CieiRfoi полиномов числителя в здаменателя отличаются на I.

Существует несколько способов реализации двухполюсников по данной Zip), удовлетворяющей перечисча1ным в § 1а2 условиям. Т, основных способа реализации рассмотрены в § 10.3-10.5.

§ Ю.З. Реалязацмя двухполюсников лестничной (цепной)

Познакомимся с понятием ншрерывнс ! дроби. Непрерывной

иазьшаюг ;фобь вцдз

Входаое аяфогивлядае или входная проводимость лестничной (цеп-нон) схемы по типу рис. 1о.1, а, в котхфой продольные озпрогавяшия названы Zj, Z3, Zb, ... и поперечные проводимостн-У yT, У, могут быть представлены непрерывной дробью.

Для того чтобы убедиться в этом, проделаем небольшие выкладки. Найдш входную проводимость правой частя схемы по отношению к зажимам тп. Она равна-Ц-. Суммарная прсеоишостъ правей!

части схемы по отношенню к зажимам тп с учетом ветан с проводимостью равна y + ~-р-. Входное сопротивление по слношаняо

к тем же зажимам

у*+-

Далее определим входное сопротиьпмие всей схемы, равное

(10.2)

Таким образом, возникает задача о переходе от (10,1) к (10,2), т. е. задача о последжагсльнсм употядоченном определении элементе* лестничной схемы (Z Z3,К Y Ye,...) по выражению (10.1), С этой целью:

1) располагаем полиномы N{p) к М(р) либо по убывающим,

по возрастающим степеням р;

2) делим многочлен на многочлен, следя за тем, чтобы в процессе деления получись положительные (не отрицательные) слагаемые и чтобы они не содержали р в степени больше 1;

3) учитываем, что если в процессе деления возникнет необходимость Перейти от расположения полиюмое по убывающим степшям к пас-положению их по возрастающим степеням, то эта операция -допустима. е следует

При делении полинома N на полином М будет тюлучена. досгигают и остаток Oi/M, т. е. Itfw

Прн делении M/Oi будет получено частное Vj,B обМток - р-

Поэтому = У,Н--

На основании изложенного npollecc последот1ательного i элементов можно представить следующей схемой:

Пример 112. Определ1Пь параметры лестничных схем. для иггар- i рааюлвггя сначала прн деления полиномы по уб вающнм. а затем (для реализация второй схемы) по Бозра< степеням р. Как булет видно из дальнейшего, в процессе i в обоих случаях пе возникнет яобходимости в переходе ог распо жения по убывающим к расположению по возрастающим степеням

Решение. Производим деление, расположив слагаемые по вающим степеням р:

§ 10.3. Pqo.l, б изображена схема и на ней указанысоотвепг Поаиакомимся ах.зната1ИЯ Щду1Ш(Вност%& н емкостей, полу?

прн депевня, Еогда иигаемые выли расположены по увывающии сге-веням р .

Схема и параметры для второго случая, когда при делении слагаемые расположены по вшрастаювшм степеням р, даны на рис 10.1, е.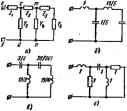

Рассмотрим далее гример, который нвдяегся иллюстрацией того, что иногда в процессе деления возникает веобходимость вамеаени во-радка расположения слагаемых.

Прим ИЗ. Требуется реализовать лестничной схемой

Решение.

г,.. !£!+?£1±?Р±1.

?p+3p>+2p+lv+2;.+l 2p+2p4-p I p-.z.

2p+2p+I

ооршцать вгашаппе из то, то надуктивяостя в емкое в примерах досгигшот npj m,ecKH ч>удно осущестаимых начетШ. Kpew того, реаащеш шесь гМ можно рассматривать как нормированные т частоте и еелшине Гсм 10 Й

>ьным, осуществить которые практически уже ие состлвиг зэтруяиеанй.

Так как получаем отрицательные слагаемые, дальнейшее №я прекращаем и пд>еходим к расположению по возрастающим степенны f

+p+p

Ha pHC. 10.1, a изображена сооггветствующая схша.

В заключение ошетим, что могут встретиться такие Z(p), ifa рые невозможно представить лестничной схемой. В этом случае vpt меишот второй способ реализации, описанный в § 10.4. [Второй си соб применяют ие только в случае невозможности 1федставления лестничной схемой.]

Еслн и он окажется неприменимым (натфимер, при юзмплахмЛ нулях и полюсах), то следует воспользоваться методом Бруне(см.§ Ю.

§ 10.4, Реализащ1я двухполюсников путем последо) деления простейших составляющих. В качестве введения ко Bnv способу реализации двухполюсника запишем операторные conpont. пня для простейших одно- и двухэлементных двухполюсников, рис. 10.2, а - д изображены простейшие двухполюсники и зап соогвегсгвующие им операторные сопротивления; на рнс. 10.2, е, ж смфотивления и проводимосга и на рис. 10.2, з-прадодимосгь. > рис. 10,2, а С= для рнс. Ю,2, б 1=0, для рис. I0.S, в 2ai = 1/С и o)J = l/(Z.ftC*). для рис. 10.2. гсА=7?ь и т Нь/Ц, ; рис. 10.2,.а Ь=1/С и d=\iRC.

Сушдость метода состоит в том, что заданное Z {р) в Biute (рис 10.3, а)

Z( -a++2p+i(P>-Первому слагаемому cjj соответствует последовательно нвдуктнвнопъ с второму -последовательная емкость Цсо. Каж слагашому вида -л- соотвегсгвует послсдовател! параллельный резонансный контур; слагашс (у - пара i

Pi. = ±M. находяиу1хся на мнимой оси плоскости р). CtmponiBfleeJ iSp) У>**е не содэжит полюсов иа мнимой осн. Функ1и1ю Z, (/>), q полюсов которой нет полюсов, находящихся на мнимой оси, наз;* функцией шншишного реактивного свпрвттяения. Вошожны с дающие варианты для Zj(p) *:

Б пунктах aj -В) полагаеи, что в н положительны.

а) 2rj(p)=2j;. * случае его осуществляют посяедиа-дьным соединенна! двухполюсников рис, 10.2, г;

, t га,Р

б) Zi (р) == 21 + Z, {р) реализуют в виде активного сопротивления бе и посяедовагелыю с ним соединенных двухполюсников рис. 10.2, а; *

Рис. 10.3

в) Z(p) = b. осушесгвликтт в виде активной) сопролпшения V Инцукпиносп. а,- lim ?И(р с. 10.3,0).

Ветичину а, в схеме рис. 10.3, а определиюг как интегральный .вычет функции Z(p)= в полюсе р-0:

ao-ResZ0,) W(0)/M-(O).