Формула (9.8) 1д)едставляет собой комШ1№Сиую форму записи Фурье, Текущий индекс k может принимать все целые числовые j чевня от -со до +о0. но ие может равняться нулю, так как пщ янная составляющая рпда выделена в виде отдельного слагаемой

Пример 109. Представить функцию f(0-=2 + 3sm(o)o( + 3aj + 2sin(2iBof -45 ) в комплексной форме записи. ,

Решение. Д,-2; Л = Зеэ>°*А 1-.Зе-3 °; Л = 2е-/ = 2е/ -; НО = 2+2j ре +зот зе- /(* .+зо )+2е г - ]

Составим выражшве для комшгахнЫ* амплитуды Л . По qiT:, лению [см. формулу (9.6)],

At = ЛйС** = At cos 4=4+jAk sin % = л;+/Лг.

где Ak определяется формулой (9.3), Ла-формулой (9.4).

Подставим правые части формул (9.3) и (9.4) в формулу (9.9): С

т/2 -V/2

f(tHC0Sk(i)at~ jsmk(iiot)dt

Пйдставим правую часть формулы (9.10) в формулу (9.8):

dt.

(9.1

п)=л+ 2 г I r[t)>dt. (9.а

-Г/2 1

§ 9.2. Спектр функции и. интеграл Фурье. Ряд Фурье - тригонометрический ряд, представляющий собой изображение п-- 4ecKcrfi функция суммой синусоид, амплитуды которых а аргументы кратны основнЫ* частоте

Под интегралом Фурье понимают тригоисактрический pim, i ставляющий непериоди>кскую функцию суммой бесконечно боль числа синусоид, амплиды которых бесконечно малы, а аргу (юседних синусоид отличаются на бесконечно малую величину.

Формулу для интеграла Фурье получают из формулы для Фурье 3 формулы (9.ПД предельным переходом-при стрем периода Т к бесконечности, v

На функцию /(f) при представлении ее интегралом Фурье i

дывают ограннташе, а именно полагают, что J f(t)dtecr[bB

конечная (не бесксжечно ббльша. Эю серьезное ограничетие. Рад фушишй эт( .угяшт-ж удсшлегасюяет *.

I Р

Так как во определению [см. формулу (9.2)], Л,= . f{t)dt. а при Т-оо 5 f(t)dt есть величина конечная, то = 0.

Преобразуем выражение f (О е-d/, стоящее под знаком

суммы в формуле (9.11). С этой целью произведение fcojo заменим паю (под ю будем понимать изменяющуюся (текущую) частоту]. В раде Фурье разность цух смежных частот А& = щ=2п/Т. Следсшатиило.

При Т-*- сх>, заменив Дш диффенциалом dw, получим

f(Oe-* d/ = g J f(t)t dt.

(9.12)

Формула (9.12) дает возможность преобразовать функвдю времени f(f) вфункци(Р частоты S(j&); преобразование (9.12) i

прямым преобразованием Фурье; а SQoi} -спектром ф1риа f{t). Это KomnaiCHan величина, задисящая от вида функции /(0. В соответствии с (9.12) в (9.11) заменим I m- dtm~S{li6)d

н учтем, что при иэненеиии k от -те до +оо ю = ЙШо также юф-няется от - оо до +оо. Следавательно, -.

и=+со

(>=i 2 S(/e>)ed .

Заменив сумму интегралом, получим

nt)-fs(ji.)< da.

(9.[3)

* Среди функций/(О, для которых интеграл J /(О Л расходится, накболее

важной дляярактшш является функция f{(}==A, где Лпостоянное число. Для 1w0 чтобы эту функцию представить интегралом Фурдальгчогся сладпощнм ярнемом. Находят интеграл вье для фуянвда f (()=Л -де Р>0 /(0=0

Р < О. Длй этоВ функции 5 tf) d{ сходится, поэтому она может- быть пред-

; ввлена иитегралом Фурье. Далее в полученной выражении устремляют р к нулю.

Формула (9,13) предстмляет собой запись интеграла фурье i мулу обратного преобразомния Фурье). Она выражает HeiwpHOL скую функцию f(t) в виде бесконечно большого числа chh)tohjv ных колебаний с бесконечно близкими частогами н бесконечно маяшл амплитудами 5(;a))dw [5(/и) конечно, но произведение бесконечно мало, так как бесконечно мала величина dbij.

В соответовни с формулой (9.13) для нахождения реакниис на любое воздействие следует его представить в виде бесконечно б шого числа гармонических воздейпвнн, символическим методом в реакцию системы на каждое из воздействий и затем просумиклч реакции на все воздеЙстыш.

rttj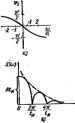

Ряс. 9.1

Преобразования (9.12) и (9.13) являются взаимно обратными i

амтмГ-гго представление фуихщи f(l) в ишшасаюй в виде интеграла Фурье [формулы (9.13)] привело к иеобходи. (Ьормально ввести сгрицатяьиую угловую частоту.

Сопоставим формулу (9.12) с формулой преобразования по Ла1

щ)И условии, что f (0 = 0 при г<0.

Если учесть, чгоИв-О при О, и заменить р на /т.тоС

переходит в (9 12). Следовательно, формулы для спектра фувкцва а

могут быть пмучиы из соогвмсгвующих формул шображео

Лапласу, если в последних р заменить на /в\

Пользуясь соогношениямя § 8.39. найдем спектр функция )

= е, полагая, что/(0-0 при 0.

Изображение по Лапласу 1/(а+р). Заменим р на /ю н получим спектр Х(/ )-1/(о.+/ш); S(/<a) есть комплексная величина, равная 5(ю)еЧ Модуль ее равен \lYa?+<sf; аргумент 4>.-an:tg[-т/о;]. Графики дпя экспоненциального импульса изображены иа рис. 9.1, , б.

Пример 110. Найти Sifo) и фв(<о) дтя прямоугольного импульса (рис. 9.1, в) амплитудой А и длительностью 4.

Решение. По формуле (9.12) находим спектр

S(,- ,)

А f е-Л-

, 1-е---

Модуль S(m)-]sin!f .

График этой функции приведен на рнс 9.1, е. Пялстиром показана огибаощая. Аргумент 9, прямоугольного импульса определим по формуле tg9,g.°* =-tg!. График показан на рис. 9.1, д. (На рис 9.1, по оси абсцесс ю.)

При значеннях ш( =я, Зя.....возрастает скачком на эт.

§ 9.3. Теорема Ре>ш. Теорему Pdlnn записывают следующим образом:

(9.15)

тл-5( }Л .

Функция f((10 при f<fl; 5(и) представляет собой модуль спектра S(/a) функции fit):

S Ф) - *J f (() e-w л, (9.16)

Если принять, что f(f) есть напряжигае, приложенное к активному сопрогааленню в 1 Ом, то левая часть в (9.15) преоставляег сабой энергию, выделяющуюся а этом сштротяалении.

Таким образом, площадь квадрата модуля спектра S(u>), разделенная на эт, является янергией, раахшаемой е аюттом сюпротт-тши, на Koimpot тздейетоЕт f (Q.

В качестве осмсБы щзи выводе теоремы Рсйли служит обратное преобразование Фурье

Умножим обе части последнего равенства иа/(/} и iHXuneipHpyeM по t от -со до +со:

J nudt J f(0 J S(/ ) *( dt-

в правой части изменим поряд<ж ннтегрнровавия:

В соответствии с формулой (9.16) следовательно.

Для перехода к формуле (9.1б> учтш, что 1фв <<0 функ1 /(f=0. Это дает возможность заменить в левой части нижний п дел с - оо на 0. Приняв во внимание, что квадрат модуля S

есть четная функция частоты, заменим J в правой части пос, уравнения ва 2 J В результате получим формулу (9Л£

§9.4. Применение спектральногометода.Спжтрвльный(частотиьйИ

метод исследования процессов в электрических цепях основан тШ испольэпйании понятии спадтров воедкпвуюищх импульсов ич4П . вых свойств цепей. Особенно широко его применяют в раднотехвяВ при рассмотрении вопросов прохождения мцоулироваяных колебапИ через усилители, фильтры и другие устройства, в им11ульснойте 1 *Н nj* рассмотрении вопросов прохождения через четырехполюсники i -ротких импульсов длительностью порчдка нескольких микросеку а в некоторых случаях даже нескольких наносекунд. Допуска-тг- что модулирсватюе колебание нли соотаетственно импульс, щсЛм Чфез четырехполюсник, иэлеиился по амплитуде, иа некоторое время I запоздал во времени, но недопустимо, чтобы существенно иа#чЛ(лм форма импульса (капебания) иа выходе по сравнению с -, импульса (колебания) на входе. Недопустимость изменения i.-, импульса (колебания) следует из того, что именно в форме импуг (колебания) заключена информация, которую он песет.

Положим, что на вхсд некоторого четырехполюсника с пфсдат * ной функцией /f(/<a) = K( )e*i J при нулевых начальных услг --воздействует сигнал fi (I), имеющий спектр S (/ш). На выходе рехполюсника появится сигнал /,(/), спектр которого

JffAtitrfdL

(9.1

Так как сигнал f,(0 может отличаться от сигналя ff) по чине (ПО амллитуде), положим в а раз, и запаздывать ва

время 0, но по форме долж ! быть таким же. как и Л (П. то можно записать, что (О = а. ( - о)-

Если к функции Л (t) применил, преобразование Фурье, то ока-i /,(0 равен

жегся, что спектр функции /, (t) равен

й5 (/о))е-/ Ч

Действительно,

(9Л8)

Введем новую переменную 1=1-1. Тетдо

S, (/и) = fle-/ f. 5 (У е- dti=ое--.5 (/ 4.

Сравнивая (9.17) и (9.18), замечаем, что

Д-(/ю)=Д-(а.)е <*1=ое-/ Ч

О1едовательно, для протождашя импульса или модул1!рованного колебания щ>ез четырехполюсник без искажения формы необходимо,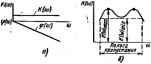

.чтобы модуль передаточной функции четырехполюсника был постоянвд (не зависел от частоты), а аргумент ч(о>)= -шГ линейно изменялся в функции частоты (рнс. 9.2, с),

В реальных четырехполюсниках эти условия могут быть выполнены лишь, приближенно в некоторой полосе частот, которую называют полосой пропускания. Полоса пропускания ограничена значениями ь>, при котсых отношение максимального значения f({a>) к минимальному равно У 2 (рис. 9.2, б). Такой характеристикой обладает, например, схема рис. 3,42, а. Для этой полосы приб-тюкенио полагают, что/С (со) = const в ф (а.)=-и/в.

Для того чтобы сигнал при прохождении через четырехполюсник не изменил своей формы, необходимо, чтобы важнейшие гармонические составляющие частотного спектра сигнала находились внутри полосы ponyoiaimfl четырехполюсника. Для импульсных сигналов треугольной, трапецеддальной, прямоугольной, колоколообразной и некоторых Других форм 1фииимают, что они занимают полосу частот, грубо говоря, от (в = 0 дэ Л1.= 2я/( , где ( -длительность импульса.