На оснований мршщипа иаложеиия решение (8.67)

[х{Щ = с1 1 *ix (©)J4-5 et J с - [Af] [г (x)ldv, J8.

где {;f(0)J -матрица начальных значений х.

Первое слагаемое в формуле (8.69) описывает свободные процгт!

в системе, второе -принужденные при нулевом исходном с-----

[вывод формулы (8.69) см. в конце параграфа].

Из (8.68) и (8.69) находим

D/(0] = [P]er ][x(0)]+{[P]elM](-fl[iV][2(T)]dT + [QJHr)].{8.

Поясним формулу (8.69) иа простом примж. Тш в с

рнс. 8.45 до коммутации был i(0J) - E/(2R). Уравнение и---

для этой схемы di/dt = - (RjL)i + (E/L), т. е.

ix} = di/dt; т = ~Я/Е; [N]=l/L, {z]=E:

Матричную функцию d-J* в формуле (8.6 вычисляют по Jn муле (leopaie) Сильвестра [13]:

(8.7Ц

(8-7-1

(?,-М

>1г,-собственные значения (характерисгическпе числа) матрицы [Ж], т. е, это корни det([M-?.[I]) = 0.

Из уравнения (8,73) следует, что ypai

Фние относительно к составляют, прнрг нулю определитель матрицы [М], в в

все элементы этсй матрицы ( = 1,..п)1 расположенные по главней диагонали, заме! няют на элементы тп-.

Характеристические числа К- это не иное, как корни характеристического уравн-; ния послекоммутациопной схемы. Запись рмпеяия в виде рада (8.711 Гфедполагает, что все харэкт(рнсгнческне числа различны ет кр* ных корней). Еслн же среди корней уравнення detMj-3,[!]) =

Рис. 8.45

будет кратный корень К 1фатносга s, те составяясшая вс-

ловленная этим ксвдш, имеег вид

где i4d/([I]-[Af])-щ)исоединенная матрица к матрице Я[1]-[MJ. В ней все элемен Qij заменены на алгебраические дополиагая. Составляющие решения по формуле (8.74) соответствуют части решения но формуле разложения (см. § 8.50), учшъшакицей кратные корни.

Пример 108. Методом-пространства состояний нсследгаать переходный процесс в схеме рис. 8.46, а. До коммутации был установившийся режим; Е = 4 В, Il А; ;? = 20Ом;£=1 Г, С=1 Ф.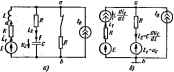

Решение. Обозначим токи и напряжения в соотаегствии с рис. 8.46, а. До коммутации

г (0-) = - = 0,5 А; ис (0 ) = +1) = 3 В.

В качестве переменных сосгояння выбираем ток tj и напряжение

на емкости uc.

Известно несколько способов составления уравнений состояния. Рассмотрим наиболее целесообразный, основанный на сведении послеком-мутационной схемы к резисгивнсй с источниками э. д. с. и тока. С этой целью индуктавноси! в нослекоммутационной схеме заменяем на источники тока, которые доставляют ток в том же направлении, что и в исходной схеме (в рассматриваемом примере L заменяем на источник тока с напряжением на нем Ldijdf). а емкости С заменяем на источники э. д. с, прячем в соответствии с теоремой Компенсации э. д. с, этих источников должны быть направлены Встречно токам в ветвях с емкостями, т. е. встречно напряжениям с на емкостях (в рассматриваемом примере емкость С с напряжением на ней Uc заменена на э. д. с. с).

В результате схема окажется без нйдуктавносгей н емкостей (Чисто резислюной), но с допопнигелмымн источниками тока и S- Д. с. (рис. 8.46, б).

в полученной резйстнвной схеме один нз узлов заземляем. С к ляем уравнения по методу узловых потенциалов и определяем п 1 циялы незазаллениьос узлов. В рассматриваемом примерено э всего один узел а. Поэтому

По известным потенциалам узлов рассчитываем на источниках тока Lk dydt, эквивалентирующих нцдуктивш н тсжи im=CmducJdt чсрсз ИСТОЧНИКИ э. Д. С, эквивалентнрую* J емкости Ст.

. Для первой ветви схемы рис, 8.46, б

. = {k-\-h)R-\-Uc=E~HR-L%

dli 2R , Uc В R

Отсюда dr=- r-Г + Т-Г*-Тсж второй ветви 1, можно отредвлить либо по первом) зак . J Кирхгофа, либо по закону Ома для участка цепи с э. д. с:

=-5Г=-fi-=--= i+/ft.

Отсюда duc/dt = (iilC) + (IkfC). Таким образом, урависшя п-ч м 1ных состояния для послексмймутациоиной схемы рис. 8.46,йт

=j-ii+0.u<:+0£+g-/

иш И=[ММ + [ЧМ, где И =

Составляем уравнение для определения характернстачеашх чисел i 4-я. -11

ilet([M-J,[I])=

Отсюда l +4+l==0; Ji=-0,27; Я -3,73<r>.

По формуле (8.72),

гА1 -SI-

По формуле (8.69),

Выполнив подсчеты, получим:

= - 1 +0.75e-c.EW+o,75e- Д; с=6 - 2,8е - Ое- з.тэ/ в.

Если за выходную величину у принять напряжение Uaj между точками d и /, то

[ i = [ R -,][ .]+[! 0][g.

Поясним переход от (8.67) к (8.69).

Решение неодйзодмяо уравнения (8.67) можно-получить в виде суммы полного решения однородного уравнения и частного реше: ния. Полное решение однородного ураввеиия

для /Э;т. где т-постоянная величиия. находим по аналогии с решением скалярного дифреии;1альнс1го уравнения х=тх х=е х (т) в виде

Подставив (8.76) в (8.75). убеждаемся в справедливосга решения однородного уравнения (8.75). Фушпщю е обозначим 1<р{1)}, а eJ*-= (f-т)]. Так как mtm+lMU++.... то №(0)1=[11.

В соответствии с методом вариации произвольных постоянных частное решение неоднородного уравнения положим в вцде

[ft,(/)=t4i((-t)lt (01Ix(T)l.

Общее решение

[*(())=t4?(*-T}IU(t)I-b№((-T))t WI l WI= =№ Otil m+l I [ Wl=(9 ((-111 [R (fib

яе IR (01 нужно определить. Подставим

I*(01=[q(-l[fi(01 (8.77)

уравнение (8.67):

[[Ф(-)1-[ЛЧ №(*-T)II [J? (OJ+tv (f--i)] IR <m~m (г]. (8.78)

(8.75)

Поскольку 1] ость матрица, столбцы которой являп

Ееявя (8.75), первый член выражения (8.78)-нулевая ыатрица. С

Пронмтегрчруем (8.79) от т ло Л

Из уравнений (8.77) и (ЯЩ следует .

1Ч> С-1)]- IX (01 (0)1-1(т)1 +1 № {J-t)l-J 11 [г Щ] di.. Но [q)(0)l=[ll. Умножая (8.81) слева на 1<р(/- )1 и учитывая, что

Гф (-т)1 Й (-т)Г=еЕ 3 с - е- I i =et J >>=[ф (/-?,)I. получим

1х(О1=1ч.((-01[л:(т)1+5 ГФ(-ад[М[г()1аХ. (8.

Полагая в (8.82) 1=0 и заменяя затем переменную X на т, получим форму*

Вопросы дяв м

I. Что понимают пад прннуждеянымн и свободными токшкя и напряжена - 2. Сформулируйте законы (правила) коммутации. 8. Дайте определение т ным и зависимым начальным условиям. 4. Объясните, почему при сое карактеристического уравнения путем приравнивания нулю входного сопр ния Zp=W(p)/Al(p) нельзя слкращать числитель и знаменатель дроби иа множитель Б. Чем определяется

ней карактервсткческого уравнения? в. I ложнте сущ1юсть классичрского метода pi чета н принцип составления уравнений определения постоянных инте1рир( 7. Дайте обоснованве обобщенным з . коммутации. 8. Запишите известные ютношеняя мечзду f(0 в f(p]. теоремы операт(ного метода и пр€,. соотношения. В. Почему р называют l , лексной частотой? Ю. Охарактеризуйте j пы расчета оператсфным методом. И.

fuc. 8.5/ ределнть переходную и импульсную i

йодную пквчднмостн (сопроткаленш функции. Укажите, с какой целью используются. 12. Охарактеризуйте идею расчета грн помонда интеграла Пюш> 13. Поясните принцип работы интегрирующих и двфференииршнх не ИпЛпТХ РУ ад я< при формировании допошяю! двухп НИКОВ? 15. Перечислите основные этапы расчета методом переменных с .- 16. Как составляют уравнення переменных состояния путем сведения пос ыутационьои схыы к чиста резнстнкной? 17. Охарактеризуйте сильные и ( IfncLrl взве<:т.шх Вам методов расчета переходных npoi 1 . Ь схеме рис. 8.47 с источником тока в момент (=0 одновременно i кается ключ лг, и замыкается Ki- Показать, что зарвды. протекояге через чввления и за время от О до со, не зависят от емкостей d и С. С лить величины этих зарядов \огшт: ° и . 1. 19. Ft

задачи 11.4; 11.12; 11.15; 11.26; 11.29; иззПГ.Зв; ПВД 11.50; UJl

глава лиятая

интеграл оурье. спвпральныя метод

§ 9.1- Рад Фурье л ношикксной ф01№1е затгсн. Как вместно из предыдущего (см. .§ 7.2), в ряд Фурье можно разложить любую лиодическую функцию f(t), удовлетворяющую уоювяям Дирихле.

Обозначим период функции Т, а осисжную частоту - ©о =2я/7. Ряд Фурье можно записать двояко.

Первая форма записи:

/№=Л+2 (м)

к= I

вторая форма записи:

/ (О = а + 2 i si +COS кщ1), (9. la)

* = I

где j4 -постоянная составляющая ряда; 4*-амплида ft-гармотики ряда; -начальная фаза ft-гармоники;

ft=- ( f(t)cosktdt. (9.4)

Из курса математики известно, что sinAr=(e-е-*)/(2у). Следжэгельно,

sin(/iM.( + = J-[e V+ , e-< V + .l]. (9.6)

По;щавив правую часть (формулы (9.5) в }юрмулу (9.1), получим fW=1.+ ,te V+V e- V+.Pj. (9.5а)

Обозначим:

Л = Л.еЧ (9.6)

Л =-А-*: . (9.7)

Тогда ряд (9.5а) можно записать так: