Единичной функцией ! р) фис. 8.41.6) иазьшаюг функцию, у4 ную едаиице при f>0 и равную нулю при (<а Единичная iyt ния I (-0 (рис 8.41.в) равна нулю при ОО и единице при < Функшш 1(0 и 1(-0 имеют нулевую размерность. Свойсгеа 6(;Я

Рк. 8.41

I) ш опред&пеняя 6(t) следует, что

ОО О-

л 1 (О равыа 64)уыкцШ1: dHt)/dl~ 6 (fj;

3) б-функция обладает фильтрующим действием:

f№e((- =f( 6(<- :

4) изображение по Лапласу 6-функшщ равно I:

lemtrfdii.

Единичные функции 1(1) и 1(-/) также обладают филы действием. Умножение произвольной функции f{l) иа 1 (() i произв(вевие /(() 1 (О в нуль при 0. Аналогично,

Импульсное (игольчатое) напряжение или ток в виде 6.* единичной площади записывают так: b(t)-l. Здесь единица г размерность В-с или Ас соотаетственно.

В соответствии с рис, 8.41 импульсное напряжение 1Шни- плошдди. равное 6(t)-i В-с. можно предпавигь как сумму , прямоугсшьиых импульсов: импульса напряжения 1/Дх, лстуг- в действие при ( = 0, и импульса -(1/Дт), вступающего в ; при (=Дт.

При f >-Дт и нулевых начальных условиях ток на входе Ц- при ВОЗДЕЙСТВИИ на нее иаприжения в виде й-функтщн i(i)s=ljj

Разложив g(t~Ax) в рцд Тейлора по степеням Дт и уч-р малость Ах, получим

тяе (t) -импульсная переходная проводимость. Для момекгов времени (Дт она численно равна току в цепи при воздействии иа цепь напряжения в виде 6-функции.

Обратим внимание иа то, что в двух формах записи интеграла Дюамеця (формулы р.бЗа) и (8.636)] используется импульсная переходная щкмзодимостъ.

Наряду с понятиями переходная проводилюсть g(t) и импульсная пфеходная проводимость (() применяют дуальные им понятия: переходшзе сопротивление r{i) и импульсное переходное ах1р(жпивлете г (О- Переходное сшротивлеиие г ь (О численно равно напряжтаию на входе цепи об (О прк воздействии иа ее вход единичным током: utm = \ Аг б(0.

Импульсное пюидаое сопротивление ra,(t) численно равно напряжению иа входе цепи ubifi, после того как иа её вход воздейсгао-вал импульс т(жа в виде 6-функции едшичной площадао;

й0=6(0-1 (А.с>-(().

Величины г (О и г {t) могут быть входными и взаимными.

§8.62. Обобщенные кцяи и иж лршяевевие расчету пдкяоднйж процессов. 06обтн ыми функциями (ОФ) [19Г221 называет фуйшйГвременГпЧ. которые терпят разрыв, наприйёр, при /=0 Значение функции прн t<0 обозначим \Ц (t), при *>0 /+((> (рнс. 8.41.е). Имея в виду фвлырукшее свойство единичных функцвй, можно записать

в общем случае / [1} может содержать также в-функцйю и ее произесщтс. Производная от

= /1(0 i {-О+/4. (О 1(0 +

Используя ОФ. можно решать задмя иа пЧ)еходные процессы, о которых -. в § 8.28, а также Задачи иа Т1мпульсние воздействия- В этом случае о составить уравненая для послекшмутжиоинсА схемы, выразить тисн, -Ш и иж пршзводныс через ОФ и, .-воспользовавишсь фильтруюпшн 1(-0. 1(0 н 6(0. приравнять в этих уравнениях коэффициента, содержащие только I (-0. только 1 итолько 6(0,а Пример 105. Путем исполъэоввння обобщенных ф пера 86 (см. рис. 8.24).

Решенн*. В уравненве для г.

ешнть задачу при*

iKKOMMi-rauHOKHoR схемы .)+ =£ (а)

подставим: 4-0-)-Kc.i.(О 1 (0:

с.= с(0 (-0+Ис,(0 1 (0: й.=с.-(0 1(-0+ а+(0 (0+б(0( с.( ,)-ис(0-)]; .= £.-[0 t-O-b £.(0 (0+в(0(%г(0+)- сЕ(0-));

c-eu-0+Hi(0.

1ЬоэффМ1Реяты. яри 1 (-/), 1 (О в W д от хрв урвпенвя

классический вли операкгаш методом, имея в виду, что Ис(0=Кс,л- В резущтате получави тот же ответ, что в в примере 86.

§ 8.63.Дополняющиедвухполюсннки.Двадвухполюсника,о, . щие R, L, С, называют дополняющими, если входное сопропт/Енне г их последовательном (параллельном) соединении оказывается чисто актйвЯ ным, не завдсящнм от ксмнлекской частоты р. Так. двух

и t/eux-вадяое н выходное i

нз параллелыю соединенных L и и двухполюсник из пар; соединенных С и (рис. 8.42, а) являются дополняющими при : последсжателсдом соединении и выполнении условия RRR -= YLiC. Двухполюсники R, С н Ri,L при их параллельном соад! нении (рис. 8.42 6) являются дополняющими при том же условии!

Элементы двух дополннкяцих двухполюсников взаимно дуалыШШ Элементам L, Q, Ri одного соответстпуют такие дуальные элементы С J ia, Ra дсяюпиякшцего, что проиэведагее сонротавтений двух взанм 9 дуальных алементов должно быть равно R, где R - пронзволь , активное сопротивлшие.

Последовательное соединение L, н Q в нсхощсм двухполюсн:п заменяется на параллельное соединетне C = Li/RKL~CJiajion я няющем. Параллельное соединение н jC, в исходном двухлолюа1.ш заменяется на последжательное соединение L-CJi и -L в дополняющем.

§ 8.64. Понятие о иедатачныя функциях и частотных :

авеньев и систем. Нередко, особенно в задачах автоматического регул .,

системы, и о характере перехощюго процесса в вей суд*т яо w г

стены. Принято расчленять систему на отдельные в

Каждое звено можно схематически (рис. Б.43, о) либо в

рмдставигь в виде некоторого чстьф4 1ивн начертании (рнс. 8.43.(9. 4

ними (л, и выходиымн { велачнншв могут ыть как электрпческве. н мер ток. напряжение, заряд, так и неэлектрическне величины, например изта или скорость перемещения какого-лвСо -кал механической системы.

На рис. 8.43, о , ,

ия была схема внутренних соединений каждого звена, всегда ь величину выразить через входную;

*. (Р)=К(Р)*и(р). (8-64)

Какова Си io выходную

Передаточная фужция от схемы внутренних сюейнв на и является функцией комплексе частоты р.

Пример 1в6, Соетавяи. К четырехполюсника рис. 8,44, а.

Решение. С в* 1ятие -

. , -ОЧной функВДн звена тесяо связано понятна

частотной характершликн звена. Последнюю получают нз выраженяя для iC (p)i заменив р ив /о;

где ю-угловая часгета; К -кшмжсное число, которое может бьггь и в алгебраической и ноказате* ной формах:

(8.66J

Зависимосп. Ll=f(e>) на: хщшгщзистияой, К=/{Ц-

, называют действительной (еещ {а}-мнимой I - -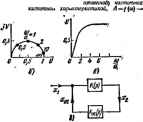

Рис. 8.44

омплитудной чаапотной характеристикой, ф=/(ц)(-фазовой чш:тотной тракте-ристикой, A=f&)-л№яpuфмwecкoй частотной характериШикой, Зависимость ЛеЧ=/(ы), построенную в полярных координатах, агыаакп амплитудно-фазовой

Пример 107. Построить в координатах U, jV патах V. ю заввсимость V=fpa) для чеГыре)[полюспнка рнс. Решение. В выражении К(р)-р/{р+а) зяменим р ие

Таяям образсм, 1;=!=ш(1*+© н

Придавая со различные значения, например а/а=0; 0,6; I; S; 10;... , н подсчитать и в V и построшь на комплексной плоскости зависимость /C(j = /((0) в декартовой системе координат (рис. 8.44, б). На рнс. 8.44, е птсград вещественная частотная характеристика U=fbit) для четырехпо) рнс. 8,44, й.

Частотные характеристика отдельных звеньев и всей системы в целом i

опредять либо расчетным путем, если известны схемы виутреннвх соедн

звеньев и зваченвя параметров, либо опытным путем. При их опытном опреж НИИ поступают следующим образом; ва вход звена (системы в цело!, свнусоцдвльное напряжение неизменной амплитуды и. изменяя частоту с до аксимЕ.гьно ьозмоншот (теоретически до бесконечности), опредаляют в и фазу выхооноО вичины.

Оптапение амплитуды выходной величины к амплитуде вкодаой дает з ние А. а сдвиг по фазе выхоцноП величины по отношению ко иходной-значение д

Вернемся к шшросу о HejicjToHHbix фу1гнциях. Положим, что система с 3(жана неаюлькнми последов;н;льно соедиленными звеньями, например

tc. 8.44,. Пусть Ki(p)-передаточная функции первого звена; Ка(-вт (р>-третьего.

Тогда операторные изображения выходных величин звеньев можно в через операторные изображения вхсщных следующим (Йразон:

Jlfia того чтобы в вуюд;,(р), перемножи

разить выходную величину всей системы Xj (р) через вх<4 (а), (б), (в). Получим

X, (р) хэ (р) Xi (р) (р) Ki (р) н (Р) Ks (р) xs (р) К, М. **(р)=(р)К(р): K(p)=iCi(p)K,(;K,(P).

Таким образом, для пол]

йфуш

телько включенных звеньев следует перемножить первдат звеньев (полагаем, что K t не зависит от п звна).

На рис. 8.44. д Еэомкеяа зятеиутав система (система с обратной с Она состоит из основного звена с передаточной функцией К {р) и звена oOpai связи с передаточной функцией /С,; {fff. Роль последнего часто выполняет у тель, работающие в режиме пропорционального уснлашя. В с с jiBc. 8.44, д

*ос(р) = Сос(; Хз( и X3lfft-Klp)lXilffi+X(m

Знак минус в знаменателе , -отрицательной статной BiHofi связи).

Если значение Кое (р) выбрано звтоколебания (амплитуда

при отсутствии входного сигиала xi-

ительной обратной связи, s полярность иа вьикме г

ак. что 1-К(р)К (р)=0, то в си

\ ограничивается ие линейностью с

§ 8.65. Снскмные функции .м поиятне о видах ч

функции н (р)-это I

додюснви. Ими ысгут быть, например, передаточная функция напряжения (7 (p)/(/i (Р), кередеточная функция тока /g (р) (р) и т. п. Если иакЫ1-либо параметр ( , L. С) в схеме четырехполюсника иэвдннетея, то нленяегся модуль я аргумент системной функции и можно говорить о чувствительности системной функойи к изменению атого параметра. Под классшеской --

Применительно к устансжившемуся сивусщдальнсму режиму говорят о чшт. еишельноста модуля и чувствОтеяьности армаат И (/Ц.

В отношении резонансных систем с высокой добротностью пользуются поня-чвеч корневой чуваязшпслыюсти, имея в виду чувствительность (р) к изменению положения нуля или полюса этой функции, находящегося вблизи мнимой оси плотности кшплексной частоты. Понятне чувствительности используют главным образом в задачах синтеза. Электрические цепн стремятся сформировать так, чтобы онн были по возможноста кало чувставтелыгы к изменению параметра.

§ 8.66. Метод пространства состояний. Метод пространства состояний (метод переменных состояния) представляет собой упорадочеяныВ способ нахождения состояния системы в функции времени, использующий матричный метод решения системы днфффенцнальных уравнений перж)го порядка, записанных в форме Коши (в нормальной форме). Примаштельно к электрическим цепям под жременными состояния понимают обычно величины, определяющие энергетическое состояние непи, т. е. токи через иадуктивноста и напряжения на емкостях (независимые начальные значения). Значения этих величин полагаем .известными к началу процесса. Пер аенпые состояния в обобщенном смысле обозначим х. Так как это некоторые функции времени, то кх можно обозначить x{t).

Пусть в системе п переменных состояния. Матрицу-столбец переменных состояния в л-мериом пространстве сосгояннй обозначим

т выходных величин (токи, напряжения) назовем у.

: иазвавяе фуикций, жч>актс])изук 1щд чегы/<

матрицу-столбец выходных величин-[(/]=

ItooNHKKH вседебстБНЙ (источники э. д. с.и тока) будо! нмено-вать г. Матрица-столбец источников воздействий [z\= .

Для электрических цепей можно составить матричные уравнения i} = iMl[x] + [N)[z}. (8.67)

{yli = iPm + iQm. <8.68)

где [Щ [Щ, [Р], [QJ-некоторые матрицы, определяемые структурой

Депи и значешшми ее irapaweipOB.