Даяное равепстоо отндетельствует раняегсн теорема еяаимноети. Для

го иа переяодные продессы сграняегся теорема еааимносгт. Для несходных проце<;соБ теорема б аруется следукицнм образом (см. ескелегныеэ схемы рис. 8.33): 1лектр8ческой депп ток переходного npouecca А-вегви i), {(), вь к э.Д-с. £ {/J в /п-ветвь (рнс. вЗЗ, а), равен току переходного ш (О Б л1-ветв , вызываемому вклю<1ециеы эс. е/ if) в к-ветъь (рис. ври условии, чтосй(0=еп.(0-

§ 8.52. Понятне о леретщюй функции по яапряжсяню.

шдалючении линейной электрической naiH с нулевыми иачалы1№ условиями к постоянному напряжению < между какими-то двумя точками и и Ь сх< мы позникаег напряжение иь (f), являюииее ся функцией времени и пропорциона. f U ~ воздейсТБующа1у напряжению U:

Ряс. 8.34 где h{t)~ переходная функция по

жению. Это безразмерная величина, денно равная напряжению !между точками а к Ь схемы, если i вход подать постоянное напряжение в I В; h{t), так же как н £(( можно определить либо расчетным, либо опытным путем.

Пример 97. Определить переходную прсеоднмость схемы рис. 8. Решение. При замыкании ключа

По определению, переходная проводимость равна току в при £ = 1 В. Стедовательно,

g(0-(l-e-?).

Примф 98. Найти собственную переходную проводимость i . В тви gi,(0, взаимную периюдную проводимость меищу третьей i ,первой ветвями g- (Q и переходную ф>тжцюо напряжения на ксвада торе hu (О для схемы рис. 8.34. Параметры с.\емы; = 1000 < )?s = 2000 Ом; С =50 ыкФ.

Решение. По определению,

С помощью классического метода спрецелим:

Полагая в этих формулах Е=1 В, нахЬдим:

Подстаисвка числовых значетий дает:

gu (О = 0,00033 + 0,000б7е-* См;

№=0.001е- См: ft c (0=4(1-е-П

Примф 99. Определить взаимную переходную провоцтюсть между первой и третьей ветвями схемы рис. 8.4, а при включении источника Э.Д.С- в первую ветвь и следующих ятачениях параметров:

Ri-BlOO Ом; £,= 1Г; С = 500 мкФ.

Решение. Изображение тока третьей ветвн

М(рГ

Корни уравнения VH(p) = 0 (см. пример 76):

р=--100+jlOO сг-1; ра=-lOO-ylOO сЧ

Полагаем £ = 1 В и в соотвегдвни с формулой раздажвщя находим

После подстановки значений параметрсв, корней pi и Ра и использования формулы (Б*-*)/(2j) = sinj: получим

gsi (О = а (О = 0,01е- < sin \т См.

првС=]В

Таким образом, взаимная переходная проводимость между третьей и первой ветвями схшы рнс. 8.4, а п]Ж данных значениях параметров как функция времени представляет собой затухающую си-нусонпу.

Пример 100. В схеме рис. 8.35 и(0== 170sin(314+30 ) В; = = 10 Ом; йз=5 0м; /?з = 5 0м; /., = 30мГ; LsSOmF; Ж = 25мГ. Найти ii(0 с помощью формулы разложения.

Рнс 8.35

Решение. Составим уравнения по методу коитурвых т У (р) [Я, +/?,+р (L, + + 2Л1)1 -/а (р) Р (ia + Л)] = (7 (р);

-/1(Л)[К.+р(-.-ЬЩ + /=(Р)(ЛаЧ-Л8+/7/.=0. Совместное их решение дает

Корни уравнения М(р)=0;

p,= 314j, р,=-2860 и р,-114сг ; ЛГ (pj = 0.000876р+2,6р + 275 + Ср - /ш) (0,00175р + 2,6); N (р,) = 170еЧ1 (20 + 0,05 314j) - 4301е -, (p,)=17flci> -(20-0,es-2860)-123-170en ; (р j = 170eW (20 - 0,05 114) = 14,29 170e i-: Af (pj=0.000875-314+2.314;+275=188,7+j817= m(pO=6890+j755=бЭЗОе - ; M(p J -284 - 75 ;=806e- .

= Im {5,13e It--m+з.03еWe-= +3,0!e? °e- = = S.I3siii(u><-8W)- Мбе-оЧ l,97e- A.

§ 8.53. Интеграл Дюамеля. Познакомимся с третьим методом р т чета переходных процессов в линейных электрических цепх -рас* том с помощью интеграла Дюам..

При нспольэшании HHrerpJri Дюамеля усжшимся переменну по котфой производится интег! рсжание, обоэиачитъ т, а под П прежнему понимать тот мс времени, в который требуется и. ток в цепн. Пусть к цепн с ну) вымн начальными условиями в в мент временя /=0 n(v?ano4air иапряженне u{i) (рис. 8.36).

Для Того чтобы иайти ток цепи в момент Зфеменн t, замен плавную кривую ступенчатой и юсумьвфуш токн от начала напряжения й(0) и от всех ступенек напряжения, вступающих в j сгвие с запозданием во временя.

Напряжение о(0) в момент вриленя t вызовет в цепи тш и(0)д{Щ где g (О -переходная проводимость.

В момент времени т+Дт (рис. 8.36) возникает скачок напря: ния йи<=ь;-Дт = и(т)Дт.

Для того чтобы найти составляющую тока в момент вршенн I вызываемую этим скачком напряжения Дм, необходимо ы(т)Дт уи J жить на значение переходной проводимости с учетом времени j ствия скачка до монета временя t

Из рис. 8.36 ввдно, что это время равно т -Дт. С . пркращЕмне тс а от этого скачка равно т-Дт)Дх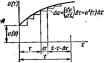

Рис 8.36

Полный ток в момент времени t палутам, еслн гфосуммнруем в<ж частичные токи от отдельных скачков и прибавим их к току u{0)g{t):

i (О = uQ)gi()+u )g(t-~ Дт) Дт.

Число членов суммы равно числу ступенек напряжения. Очевидно, что ступенчатая кривая тем лучше заменяет плавную кривую, ч€м больше число ступенек. С этой целью заменим конечный интервал времени Дт на бесконечно малый dx и пд)евдем от суммы к интегралу:

Ht)=u(O)g(f)+lu-{,0g{t-x)dx,

Формулу (8.63) назьшают интегралом Дюамеля.

Приведем еще пять форм запясн интеграла Дюамеля. !. Интеграл в (8.63) возьмем во частям;

udvuv-vdu; и* (и) dTda; g((-тЗ=ы;

И Ш (l-x)dzg[t-T) и (т) + (т)е (*iO<JT

(0) и (О -g (О U (OJ+1U fx) е (/-Odr.

Педставнв результат в (8.63), получим

* (0 (Ое(0)+1 (t)e (/-1) dx.

(8.63)

(8.63:

2. Для любых двух ф>нкций ft (О и h путем заме доказапь справедливость следующего соотношенаж

Распространив это соотношенне записи интеграла Дюамеля:

I в (8.63, получим еще две формы

3. Имет в виду формулу 5/(Аг, adx по параметру i

,(0=0 (Ое (0)+J (*-tJe (х) ох; (8.636)

i (0=в (0) g (0+J и it~g (t) dx. £8.63bJ

Пвронапня определенвого интеграла С (aJ =

и уявтывая соотношение (я), запишем еще две формы написи: /

Два последних соотиошенип имеют непосредственное отношение к свертки операторного метода: еслн fi(p)/i(0 и fs(p)=/s(0. то

Fi(rtf(p) = J/tW/sP-t)dT;

с пшощью интеграла Дюамеля можно найти не только ж, и любую другую физическую величину, например напряжение. В j случае в формулу вместо перасодной проводимости g(t) будег i переходаая функция h{t).

§ 8.54. Последовательность расчета с помощью интеграла J меля. Расчет с помощью интеграла Дюамеля проводят в четыре s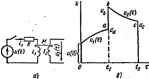

1) (шределшне переходной проводимости g(f) Переходной функш h(t)) для исследуемой цепи;

2) -определенве g{t-T) [hit-i)]. С этой целью в формуле ; 8(0 [ft(OJ заменяют / на (/ -т);

3) опрсделеине и Для этого находят щкшводную от э . ного напряжения и (t) по времени ( и в полученном выражении зам вяют t на т;

4) подстангта£а найденных на этапах 1, 2, 3 функций в формул] <8.63), интегрирование по переменной т и подстановка пределов.

Прнм 101. Найти i-f{t) и йа=/(0 при включении ил1 . в схеме рис 8.37, а. Напряжение встснника э. д. с. u(t) < = JOO(l-er) В; й = 0.25 с ; R = 0,5 Om;L,= I Г; М~0,5 Г.

Решение. ПЕрехрдаая проводимость цепи, состоящй из последовательно включенных R и L, g(/)=i.(-e-*), где bPjLxi

Первое слагаемое в формуле (8.63) выпадает, так как и(0) =а При этом

и (/) = !00(1 -е-°0= lOOae-: и (т) = ЮОяеЧ

1Л0 = I и (т) g Р - т) Л= I е [1 - е-* dt.

П1И интегрировании учитываем, что е-* от г не зависит: f, (О=200(1+6-0.и 2е-о.25) Д. Напряжение на зажимах вторичной обмотки

%(0=Л1 -=50(е- .= -е-<.и) В.

§ 8.55. Применение интеграла Дюамеля при сложной форме напряжения. Пусть напряжение и(т) иэметяется во времени по слож-тщ закону, Harj)HMqj в соответствий с рис. 8,37, б. Начальное напряжение равно и(0). В интервале от т=0 до т = /, напряжение планно расгег, и-закон его изменения в этом интервале времени u(t). В момент rti оно меняется скачком от до и, а затем снова плавно растет, но уже По другому закону (т) во времени по сравнению с первым интервалом. При т = напряжение скачком уменьшается от значения до нуля.

Требуется найтн ток в каждом нз трех интервалов времени. Под ne[tBbiM интервалом будем понимать интервал времени от т=0 до т = /, (не включая скачка напряжения от до и; под вторым-от до 4 включая скачок от до и, но не включая скачок от Uc до О, под третьим -при т>-, включая скачок от до 0.

Интегрирование по-прежнему проводим по т, понимая под t фиксированный момент времво!, в который требуется найти тсж. Ток в любой момент времени t опредашгся действием всех напряжений, воздействующих иа цепь до момента L

В первый интервал времени

i(t)==u(0)gitH-{f[(r)g(t-T)dt. Во втсфой интервал времени

+( 6 - .)g С - О+S 4 wif ( - <)