Решение. Положительные иаправленвя токов в легеях принимаем в соотаегствии с рис. 1.14, а. С помощью схемы рис. 1 М. б (ипочяик 5лс, удален и зажимы ей закорочены) находим ики в вег-вях от действия источника тока:

используя схему рис. 1.14, в, подсчитываем токи в ветвях от действия источника 9.Д.С. (зажимы сЬ разомкнуты, так как внутреннее сопротивление иаочшша тока равно бесконечности):

Результирующие токи в ветвях найдем, алгебраически <гммнруя соответствующие частичные токи этих двух режимов;

/1 = / + Л = 5--0-5 А; /, = /a-/S = 3 21 А; /. = /з + /з = 2 + 2 = 4 А; 4>a=4>t + hR> + / А: i; j = l.4 + 5-2=14 В. Мощность, доставляемая в схему нсточником тока, 1/ ь/й = 14-5=ч = 70 Вт. Мощность, доставляемая в схему источником э.д.с., EL = 20-4 = 80 Вт.

Уравнение баланса мошностя IVii + IlR + HRi-UobU+EIa.

§ 1.15. Входные и взаимные проводимости ветвей. Входное сопротивленне. Не рис. 1.15, а изображена так называемая скелет-тя схема пассивной цепи. На ней показаны только ветви и узлы.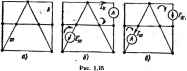

В каждой ветви имеется сопротивление. Вцделим в схеме две ветви: одну из них назовем ветвью т, другую-ветвью к. Поместим в ветвь -Д-с Е (других Э.Д.С. в схеме нет;. Выберем контуры в схеме так. чтобы ft-Bb входила только в fe-контур. а т-вегвь-только в т-кипур. Э.Д.С. т вызовет токи в ветвях кит: hEj,; \ I. = E.J Коэффициенты g имеют размерность проводимости.

Коэффивдеят g с одинаковыми индексами называют входшя!

прозодимостью ветви (ветвн т). Он численно равен току в ветви т. возникающему от действия э.д.с. £=1 В (единичной э.д,с.): / = = l-gm.

Коэффициенты g с разными индексами называют взаимными право-дияостяма. Так, gtm есть взаимная прсжодямость fe- и т-ветвей. Взаимная проводимость gkm чименно равна току в возника-

ющему от действия единичной э.д.с. в т-ветви *.

Входные и взаимные проводимости ветвей используются при выводе общих свойств линейных электрических цепей (см. § 1.16 и 1.18) и % при расчете цепей по методу наложения [см. формулу (1.7)].

Входные и взаимные проводимости могут быть определены расчетным и опытшлм путями.

при их расчепюм определении составляют для схемы уравнения то методу контурных токов, следя за тем, чтобы ветви, взаимные и входные проводишств котфых представляют интерес, входали бы каждая только в свой контур. Далее находят определитель системы Д и по нему необходимые алгебраические дополнетня:

е..=л, Л; (1.9)

е*т=л*л. (1.10)

По формуле (1.10) gk может псшучиться либо положительной, либо отрицательной величиной. Отрицательный знак означает, чю 9.Д.С. Ет, направленная согласно с контурным током в т-ветви, вызывает ток в ft-ветви, не ( - совпацающий по направлению с произвольно вы- (Т)я

бранным направлением контурного тока h по ft-ветвп. G)fm

При опытном определении g m и в m-ветвь > г-г

схемы QiHC, 1.15, б) включают э.д.с. и в *

й-аетвь -амперметр (миллиамперметр). Поделим Рис. 1.16

ток /ft на Э.ДХ. Е и найдш значение gm. Для нахождения входной проводимости ветзн /я (g, ) необходимо измерить ток в т-ветвн, вызванный э.д.с., включашой в /и-ветвь. Частное от деления тока т-ветзн на э.д.с, т-ветви н дает

Выделим т-ветвь, обозначив всю остальную часть схемы (ие содержащую ЭЛ.С.) некоторым прямоугольником{рис 1.16). Вся схема, обозначенная прямоугольником, по отношению к зажимам аЬ обладает некоторым сопротивлением. Его называют входным сопротиям-нием. Так как в рассматриваемом примера речь вдет о входном сопротивлении для т-ветвп, то обозначим его R :

(1.11)

Входные я взаимные проводимости ветвей можно определить я иначе: входная проводимость т-ветви -это коэффициент пропорциональности между кжом этой вегаи и э.д-с. той же i

ветан (пря отсутствии э.д,с в других .

(ОСТЬ ветвей ft i ; н 9ЛС т-ветв

Таким образом, входное согфогавление т-ветвн есть величина, обратная вхощгой проводимости т-ветви. Его ие следует сманивать с полным со1фотнЕлшием т-контура в методе кштуриых токов, которое не имеет с ним ничего общего.

Пример 7. Определить входную гфовсщкмость gn и взаимную прс водимость в схеме рис. 1.13.

Решение. Контуры на схеме рис. 1.13 выбраны так, что ветвь / (ветвь сЬт) с э.д.с. входах только в ввый контур, а вегвь 2 (вегеь со) с э.д.с. £,--во второй. Поэтому можно воспользоваться опрсяелятелем системы Д и алгеаичажими дополнениями Дц и Д, составленными по данным принта Б: 1-5 -2]

-1L = 4=0,026 ОМ-..;

§ I.I6. Теорема взаимности. Теорема взаимности формулируется следукхднм образом: для любой линейной цепи пюк в k-eemea. вызванный Э.Д.С. £ , находящейся в т-ветви,

hEkm

будет равен току 1 в т-ветеи, вызванному э.д.с. £* (численно рав-ион .д.с £J, тходющйся в k-eeimu,

и = Е .

Для доказательства теоремы взаимности обратимся к рис. 1.15, о. Как и при выводах в § гавделим две ветви схемы: ветвь k и

вегвь т. Включим в ветвь m источник э.д.с. £ , в ветвь ft-амперметр А** для измерения тока /*. Пусть каждая из ветвей ft н m входит соответственно только в ft- и т-кошуры. Тогда но методу контурных токов /й = £ййлт/Д. Затем поменяем местами источник э.д.с. и амперметр, т. е. источник э.д.с. переместим из ветви т в ветвь ft и назовем тепзь £ , а амперметр -из ветви ft в ветвь т. В этом случае ток

/л, = £Дт*/Д.

Так как Е=Ет, а Д = Дй в силу симметрии определителя системы Д относительно главной диагонали (см. § 1.13), то ток /* в схеме рис. 1.15, б равняется току / в схеме рис. 1.1Ь, е.

при практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и э.д.с. в схемах рис. 1.15, б, е.

Едшива проеоврмости Otra СИ называется сйменс (См). Амперметр включаш только дяя еаглядиоси; соирошвленне анпсрметря

Еолагаем равным нулю.

Так, если э.д.с. £* источника э.д.с., находящегося в ft-ветви схемы рис. 1.15, е. направлена согласно с контурным током 7fi в схеме рис. 1.15, б, то положительное направление тока 1 в схеме рис. 1.15, е совпадает с направлением э.д.с. £ в схеме рис. 1.15,* б.

Для нелинейных цепей теорема (принцип) взаимности невыполнима. Цепи, для которых не выполняется принцип взаимности, называют необратимыми.

Пример 8. В схеме рис. Ы7 переключатели Pi, Р, Ps находятся либо в первом, либо во втором попожетии. Если они находятся в положении /, то в схеме включена толы<о одна э.д с. £. Под I действием э.д.с. Е, протекают токи /i=l,5 А, /а=3 А, /s=i А.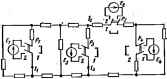

Найти ток 1а, если все переключатели находятся в положшии 2, полагая, что £ = 20 В, £ = 40 В, £ = 50 В, £,= 10 В.

Решение. Для определения тока воспользуемся тфинципом наложения и принципом, взаимности. Если бы в схеме была включена лишь одна Э.Д.С. £i= 10 В. а остальные э.д.с. (£2 и £3) отсутствовали, то в ветви 4* по пршшипу взаимности протекал бы сверху вниз ток в 1,5 А. Так как э.д.с. = 20 В, то в ветви 4 протекает ток. равный 1,5-20/10 = 3 А. Аналогичным образом огфедёлим токи в ветви 4 от действия Э.Д.С £3 и э.д.с. £3 и произведем алгефаическое сложение частичных токов (с учетом их на1Ч)авления):

/.= 1,5-+3.-1.=10 А.

§ 1.17. Теорема

В любой электрической цепи

без изменения токораспределения сопротивление можно заменить а.д.С; численно равной падению напряжения на заменяемом сопротивлении и направленной встречно току в этом сопротивления.

Для доказательства теоремы компатсации выделим из схемы о;аУ ветвь с сопротивлением R, по котсй течет ток /, а всю остальную часть схемы условно обозначим прямоугольникш (рис. 1.18, а).

Если в выделенную ветвь включить две одинаковых и противоположно направленных э.д.с. £, численно равных падению напряжения

иа~ сопротивлении /? под действием тока / (EJR; рис. 1.Д8,-6), то ток / в цепи от этого не изменится. Убедимся, что разность потенциалов между точками о и с в схеме рис, I.I8, б при этом будег равна нулю. Действительно,

c = 4> -IR+E=a~lR + IR = 4

Но если (Рсфо. то точки а и с можно объединить в одну, т. е, закоротить участок ас и получить схему рис. 1.18, е. В ней вместо сопротавления R включен источник э.д.с. Е.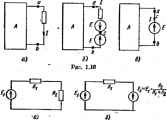

Пример 9. Убедаться в тождественности схем рис. 1.19, о, б Решение. В схеме ряс. I.I9; в ток I = £t/(Rt+R. Для схемы рис. 1.19, 6

Таким образом, замена сопротивления R на источник э.д.с. как это и следует из теоремы компенсации, не вызвала изменения тока в схеме.

§ 1.18. Линейные соот

д V : - vwinuuiruiifl в электрических цепях. Если в линейной электрической цепи изменяегся э.д.с. или сопротивление в какой-либо едкой ветви, то две любые величины (токи и напряжения) двух любых ветвей связаны друг с другом линейными зависимостями вада у=а+Ьх,

Роль X выполняет ток или напряжение одной ветви, роль у-ток или напряжение другой ветви.

Доказательство. Согласно методу контурных токов, общее выражение для тока в А-ветви записывается в вцде (1.7). Если в схеме

взменяется задлько одна э. д. с, например э. д. с. то все слагаемые в (1.7), кроме слагаемого £ g*m. постоянны и могут быть для сокращения записи заменены некоторым слагаемым А. Следовательно,

h=A, + E, . (1.12)

Аналогично, для какой-то р-ветвн

1р=А, + Ер . (1.13)

Нацдем из (1.13):

E {I,-A,)fg, и подставим в (1.12). Получим

h = a+hlp. (1.14)

ak = At~Apglgpm, bk--gkmlgpm-

Коэффициенты о* и bi, могут быть 0. В частном случае либо at, либо 6fc может бьиь равно нулю.

Равенство (1.14) свидетельствует о том, что при изменении э. д. с. токи /ft и 1р связаны линейной зависимостью. Из теоремы компенсации известно, что любое сопротивление можно заменить э. д. с.

Слеповатепьно, изменение сопротивления в т-ветви эквчважтно изменению э. д. с. £ . Таким образом, линейное соотношение между двумя любыми токами (1.14) имеет место при изменении не только э. д. с. Е , ио и сопротивли1ия какой-то т-вегпи.

Если обе части (1.12) умножить на сопротивление А етви R и проделать аиалоп4Чиые выкладки, то можно убедиться в том, что напряжение на А-ветви линейно связано с током в р-ветви.

Ксоффициенты Oft и bt из (1.14) и в других подобных выражениях могут быть найдены либо расчетным, либо опытным путем.

При опытном определении коэффициентов достаточно найти значения двух токов (или соответственно напряжений) при двух различных режимах работы схемы и затем решить систему из двух уравнений с двумя неизвестными. Пусть, например, в нервом опыте /ь = /*1 В /р = /р1, а во втором опыте Л = и /р = /ра. тогда

/fci-flfc+Wpi и /fta= ft + Wp2-

Отсюда

Если в стле одновре.менно изменяются э. д. с. или оопротнвлапи в каких-либо двух ветвях, то любые три величины в этой схеме * (токи, напряжения) связаны друг с другом линейным соотношением ецда

уа+Ьх+сг.